Subsection 10.2.1 Making a Log Scale
Because \(\log {(x)}\) grows very slowly as \(x\) increases from 1, logarithms are useful for modeling phenomena that take on a very wide range of values. For example, biologists study how metabolic functions such as heart rate are related to an animal’s weight, or mass. The table shows the mass in kilograms of several mammals.
| Animal |
Shrew |
Cat |
Wolf |
Horse |
Elephant |
Whale |
| Mass, kg |
\(~0.004~\) |
\(~~~~4~~~~\) |
\(~~~~80~~~~\) |
\(~~~300~~~\) |
\(~~~5400~~~\) |
\(~70,000~\) |
Imagine trying to scale the \(x\)-axis to show all of these values. If we set tick marks at intervals of 10,000 kg, as shown below, we can plot the mass of the whale, and maybe the elephant, but the dots for the smaller animals will be indistinguishable. (On this graph, the first dot would have to represent the shrew, cat, wolf and horse!)
On the other hand, we can plot the mass of the cat if we set tick marks at intervals of 1 kg, but the axis will have to be extremely long to include even the wolf. We cannot show the masses of all these animals on the same scale.
To get around this problem, we’ll compute the the log of each mass, and use the logs on a new scale. The table below shows the base 10 log of each animal’s mass, rounded to 2 decimal places.
| Animal |
Shrew |
Cat |
Wolf |
Horse |
Elephant |
Whale |
| Mass, kg |
\(~0.004~\) |
\(~~~~4~~~~\) |
\(~~~~80~~~~\) |
\(~~~300~~~\) |
\(~~~5400~~~\) |
\(~70,000~\) |
| Log (mass) |
\(-2.40\) |
\(0.60\) |
\(1.90\) |
\(2.48\) |
\(3.73\) |
\(4.85\) |
The logs of the masses range from \(-2.40\) to \(4.85\text{.}\) We can easily plot these values on a single scale, as shown below.
We’d need to keep in mind that we are plotting the logs of the animals’ masses, and not the actual masses. However, remember that a logarithm is really an exponent! For example, the mass of the horse is 300 kg, and
\begin{equation*}
\text{since} ~~~\log_{10}(300) = {\blert{2.48}}, ~~~\text{then} ~~~ 10^{\blert{2.48}} = 300
\end{equation*}
So instead of plotting the logs from the table, we will plot powers of 10 that give the actual masses of the animals, like this:
Compare this new scale to the previous one. It looks almost the same, except that the number line is labeled with powers of 10. Even though we computed the log of each mass, we still plotted the actual mass of each animal, in its form as a power of 10. It is the scale on the number line that has changed.
A scale labeled with powers of 10 is called a logarithmic scale, or log scale. The powers of 10 on a log scale are evenly spaced, so that the actual values at the tick marks look like this.
We can see right away that the increments between tick marks on a log scale are not equal, as they are on a usual linear scale. The increments get larger as we move from left to right on the scale. However, when we are plotting powers of 10 we use the exponents to place the data points on the scale. For example, you can check that the mass of the horse, at \(10^{2.48} = 300\) kg, is plotted about half-way between \(10^2 = 100\) and \(10^3 = 1000\) on the log scale, because 2.48 is about half-way between 2 and 3. Similarly, the mass of the cat, at \(10^{0.60} = 4\) kg, is plotted between \(10^0 = 1\) and \(10^1 = 10\) on the log scale.
Example 10.2.1.
Plot the values on a log scale. \(\alert{\text{[TK]}}~\)
| \(x\) |
\(0.0007\) |
\(0.2\) |
\(3.5\) |
\(1600\) |
\(72,000\) |
\(4 \times 10^8\) |
Solution.
We first compute the base 10 logarithm of each number.
| \(x\) |
\(0.0007\) |
\(0.2\) |
\(3.5\) |
\(1600\) |
\(72,000\) |
\(4 \times 10^8\) |
| \(\log {(x)}\) |
\(-3.15\) |
\(-0.70\) |
\(0.54\) |
\(3.20\) |
\(4.86\) |
\(8.60\) |
Then we plot each number as a power of 10, estimating its position between powers with integer exponents. For example, we plot the first value, \(10^{-3.15}\text{,}\) closer to \(10^{-3}\) than to \(10^{-4}\text{.}\) The finished plot is shown below.
Checkpoint 10.2.2. Practice 1.
Complete the table by estimating the logarithm of each point plotted on the log scale below. Then use a calculator to give a decimal value for each point.
| \(\log {(x)}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
| \(x\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
Answer.
| \(\log {(x)}\) |
\(-4\) |
\(-2.5\) |
\(1.5\) |
\(4.25\) |
| \(x\) |
\(0.0001\) |
\(0.00316\) |
\(31.6\) |
\(17,782.8\) |
Checkpoint 10.2.3. QuickCheck 1.
Fill in the blanks to complete each statement.
We use for graphing variables that take on a very wide range of values.
The tick marks on a log scale are labeled with .
To plot values on a log scale, we first compute the of the values.
A fraction less than 1 is plotted on a log scale as a power with a exponent.
Subsection 10.2.2 Labeling a Log Scale
Log scales allow us to plot a wide range of values, but there is a trade-off. Equal increments on a log scale do not correspond to equal differences in value, as they do on a linear scale. You can see this more clearly if we label the tick marks with their integer values, as well as powers of 10. The difference between \(10^1\) and \(10^0\) is \(10 - 1 = 9\text{,}\) but the difference between \(10^2\) and \(10^1\) is \(100 - 10 = 90\text{.}\)
As we move from left to right on this scale, we multiply the value at the previous tick mark by 10. Moving up by equal increments on a log scale does not add equal amounts to the values plotted; it multiplies the values by equal factors. In the next Example, observe how the integers are plotted on a log scale: they are not evenly spaced.
Example 10.2.4.
Plot the integer values 2 through 9 and 20 through 90 on a log scale.
Solution.
We compute the logarithm of each integer value.
| \(x\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
| \(\log {(x)}\) |
\(0.301\) |
\(0.477\) |
\(0.602\) |
\(0.699\) |
\(0.778\) |
\(0.845\) |
\(0.903\) |
\(0.954\) |
| \(x\) |
\(20\) |
\(30\) |
\(40\) |
\(50\) |
\(60\) |
\(70\) |
\(80\) |
\(90\) |
| \(\log {(x)}\) |
\(1.301\) |
\(1.477\) |
\(1.602\) |
\(1.699\) |
\(1.778\) |
\(1.845\) |
\(1.903\) |
\(1.954\) |
We plot the integers on a log scale, as shown below.
Notice that the spacing between the integers 2 through 9 is the same as the spacing between the integers 20 through 90.
On the log scale in
Example 10.2.4, notice how the integer values are spaced: They get closer together as they approach the next power of
\(10\text{.}\) If we would like to label a log scale with integers, we get a very different looking scale, one in which the tick marks are not evenly spaced.
Here is a log scale labeled not with powers of \(10\text{,}\) but with integer values, like this:
Some applications use log-log graph paper, which scales both axes with logarithmic scales. On the graph in the next Checkpoint, the tick marks between powers of 10 show integer values, as on the scale above.
Checkpoint 10.2.5. Practice 2.
The opening page of
Chapter 6shows the "mouse-to-elephant" curve, a graph of the metabolic rate of mammals as a function of their mass. Here it is again.
(The elephant does not appear on that graph, because its mass is too big.) The figure below shows the same function, graphed on log-log paper.
Use this graph to estimate the mass and metabolic rate for the following animals, labeled on the graph.
| Animal |
Mouse |
Dog |
Sheep |
Cow |
Elephant |
| Mass (kg) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
| Metabolic rate (kcal/day) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
Answer.
| Animal |
Mouse |
Dog |
Sheep |
Cow |
Elephant |
| Mass (kg) |
\(0.02\) |
\(15\) |
\(50\) |
\(500\) |
\(4000\) |
| Metabolic rate (kcal/day) |
\(3.5\) |
\(500\) |
\(1500\) |
\(6000\) |
\(50,000\) |
Checkpoint 10.2.6. QuickCheck 2.
Decide whether each statement is true or false.
Equal increments on a log scale correspond to equal differences in value.
Moving up by equal increments on a log scale multiplies the values by equal factors.
If we label a log scale with integers, the tick marks are evenly spaced.
On log-log graph paper, both axes are labeled with logarithmic scales.
You may have already encountered log scales in some everyday applications. In the examples that follow, don’t worry if you aren’t familiar with the science surrounding the application; we will mainly be concerned with the mathematics of using the scale.
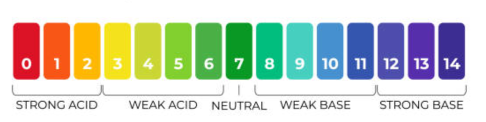
Subsection 10.2.3 Acidity and the pH Scale
You have probably heard that the pH value of most shampoo is between 7 and 9. The pH scale is a log scale used to measure the acidity of a substance or a chemical compound. Acidity depends on the concentration of hydrogen ions in the substance, denoted by \([H^+]\text{,}\) which can take on a wide range of values, from \(10^{-1}\) to \(10^{-14}\text{.}\)
To simplify the numbers we have to work with, we define the pH value by
\begin{equation*}
\text{pH}=-\log_{10}([H^+])
\end{equation*}
By taking the log of \([H^+]\) (and changing its sign), we are looking at just its exponent, so that values for pH fall between 0 and 14. A pH value of 7 indicates a neutral solution, and the lower the pH value, the more acidic the substance.
\begin{equation*}
\large{\blert{\text{Ph Scale}}}
\end{equation*}
Some common substances and their pH values are shown in the table.
| Substance |
pH |
\([H^+]\) |
| Battery acid |
\(1\) |
\(0.1\) |
| Lemon juice |
\(2\) |
\(0.01\) |
| Vinegar |
\(3\) |
\(0.001\) |
| Milk |
\(6.4\) |
\(10^{-6.4}\) |
| Baking soda |
\(8.4\) |
\(10^{-8.4}\) |
| Milk of magnesia |
\(10.5\) |
\(10^{-10.5}\) |
| Lye |
\(13\) |
\(10^{-13}\) |
Notice that the pH values are a log scale, so that a decrease of 1 on the pH scale corresponds to an increase in \([H^+]\) by a factor of 10. Thus, lemon juice is 10 times more acidic than vinegar, and battery acid is 100 times more acidic than vinegar.
Example 10.2.7.
Calculate the pH of a solution with a hydrogen ion concentration of \(3.98 \times 10^{-5}\text{.}\)
The water in a swimming pool should be maintained at a pH of 7.5. What is the hydrogen ion concentration of the water?
Solution.
We use a calculator to evaluate the pH formula with
\([H^+] = 3.98\times10^{-5}\text{.}\)
\begin{equation*}
\text{pH} = -\log_{10}{(\alert{3.98 \times 10^{-5}})} \approx 4.4
\end{equation*}
We solve the equation
\begin{equation*}
\alert{7.5} = -\log_{10}([H^+])
\end{equation*}
for \([H^+]\text{.}\) First, we write
\begin{equation*}
-7.5 = \log_{10}([H^+])
\end{equation*}
Then we convert the equation to exponential form to get
\begin{equation*}
[H^+] = 10^{-7.5}\approx 3.2 \times 10^{-8}
\end{equation*}
The hydrogen ion concentration of the water is \(3.2 \times 10^{-8}\text{.}\)
Checkpoint 10.2.8. Practice 3.
The pH of the water in a tide pool is 8.3. What is the hydrogen ion concentration of the water?
Subsection 10.2.4 Decibels
The decibel scale, used to measure the loudness of a sound, is another example of a logarithmic scale. The loudness of a sound depends on the intensity \(I\) of its sound waves, which is measured in watts per square meter. The decibel value, \(D\text{,}\) is given by
\begin{equation*}
D=10 \log_{10}\left(\frac{I}{10^{-12}}\right)
\end{equation*}
Once again, taking the log of \(I\) simplifies the numbers involved by considering just their exponents. (And dividing by \(10^{-12}\) brings the values into a convenient range.)
The table below shows the intensity of some common sounds.
| Sound |
Intensity (watts/m\(^2\)) |
Decibels |
| Whisper |
\(10^{-10}\) |
\(20\) |
| Background music |
\(10^{-8}\) |
\(40\) |
| Loud conversation |
\(10^{-6}\) |
\(60\) |
| Heavy traffic |
\(10^{-4}\) |
\(80\) |
| Jet airplane |
\(10^{-2}\) |
\(100\) |
| Thunder |
\(10^{-1}\) |
\(110\) |
Consider the ratio of the intensity of thunder to that of a whisper:
\begin{equation*}
\frac{\text{Intensity of thunder}}{\text{Intensity of a whisper}}
= \frac{10^{-1}}{10^{-10}}= 10^9
\end{equation*}
Thunder is \(10^9\text{,}\) or one billion times more intense than a whisper. It would be impossible to show such a wide range of values on a graph. When we use a log scale, however, there is a difference of only 90 decibels between a whisper and thunder.
Example 10.2.9.
Normal breathing generates about \(10^{-11}\) watts per square meter of intensity at a distance of 3 feet. Find the number of decibels for a breath 3 feet away.
Normal conversation registers at about 40 decibels. How many times more intense than breathing is normal conversation?
Solution.
We evaluate the decibel formula with
\(I = \alert{10^{-11}}\) to find
\begin{align*}
D \amp = 10 \log_{10}\left(\dfrac{\alert{10^{-11}}} {10^{-12}}\right) \amp\amp \blert{\text{Subtract exponents: }{-11}-(-12)=1}\\
\amp = 10 \log_{10} ({10^1}) = 10(1)\\
\amp = 10 \text{ decibels}
\end{align*}
The sound of breathing registers at 10 decibels.
From part (a), we know that the sound intensity of breathing is
\(10^{-11}\) watts per square meter. We’ll calculate the intensity of conversation from its decibel value.
\begin{align*}
40 \amp = 10 \log_{10}\left(\frac{I}{10^{-12}}\right) \amp\amp\blert{\text{Divide both sides by 10.}}\\
4 \amp = \log_{10}\left(\frac{I}{10^{-12}}\right) \amp\amp\blert{\text{Convert to exponential form.}}\\
\dfrac{I}{10^{-12}} \amp = 10^4 \amp\amp \blert{\text{Multiply both sides by }10^{-12}.}\\
I \amp = 10^4(10^{-12}) = 10^{-8}
\end{align*}
Finally, we compute the ratio of intensities:
\begin{equation*}
\dfrac{\text{conversation intensity}}{\text{breathing intensity}}= \frac{10^{-8}}{10^{-11}}= 10^3
\end{equation*}
Normal conversation is 1000 times more intense than breathing.
Checkpoint 10.2.10. Practice 4.
The noise of city traffic registers at about \(70\) decibels.
What is the intensity of traffic noise, in watts per square meter?
How many times more intense is traffic noise than conversation?
Answer.
\(I = 10^{-5}\) watts/m\(^2\)
\(\displaystyle 1000\)