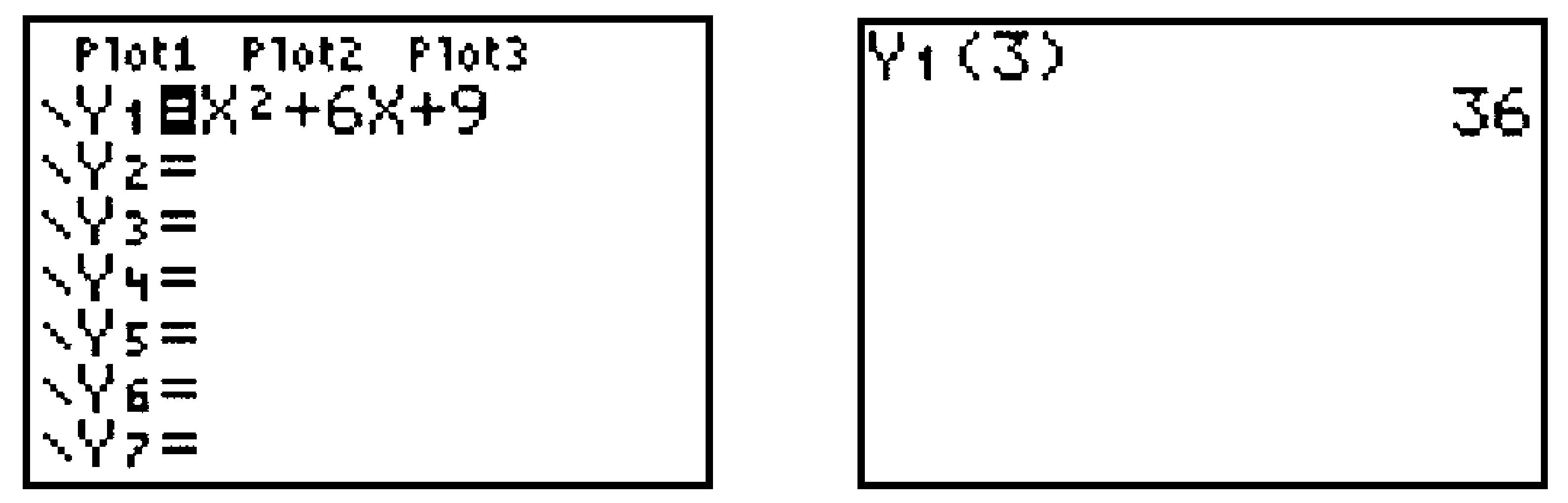
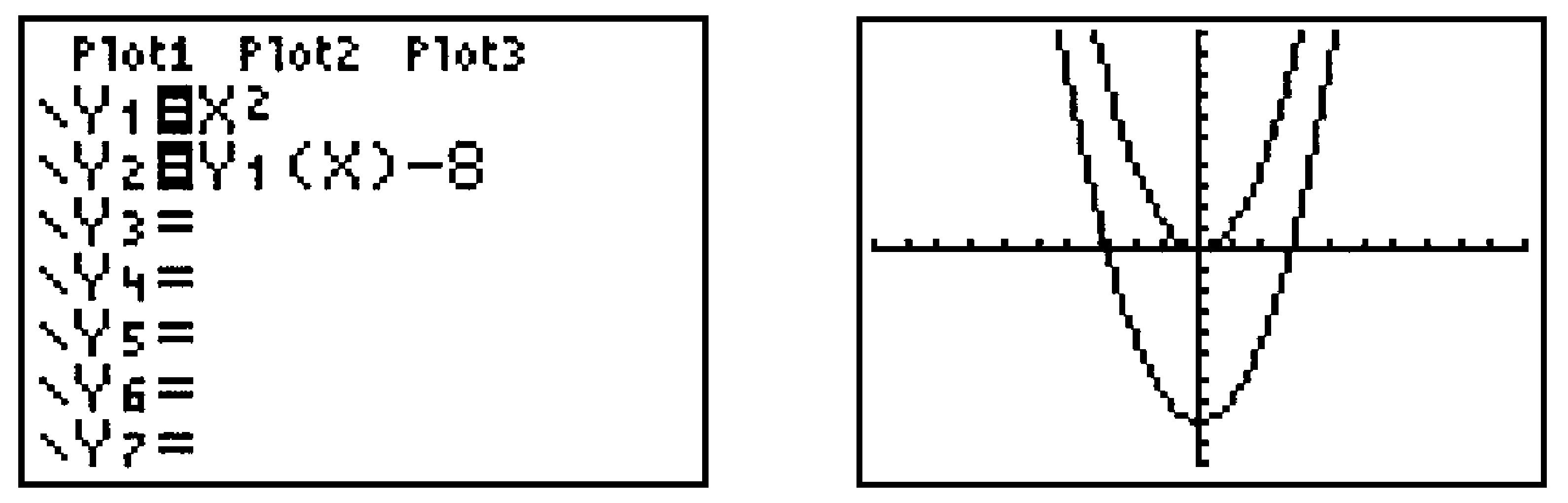
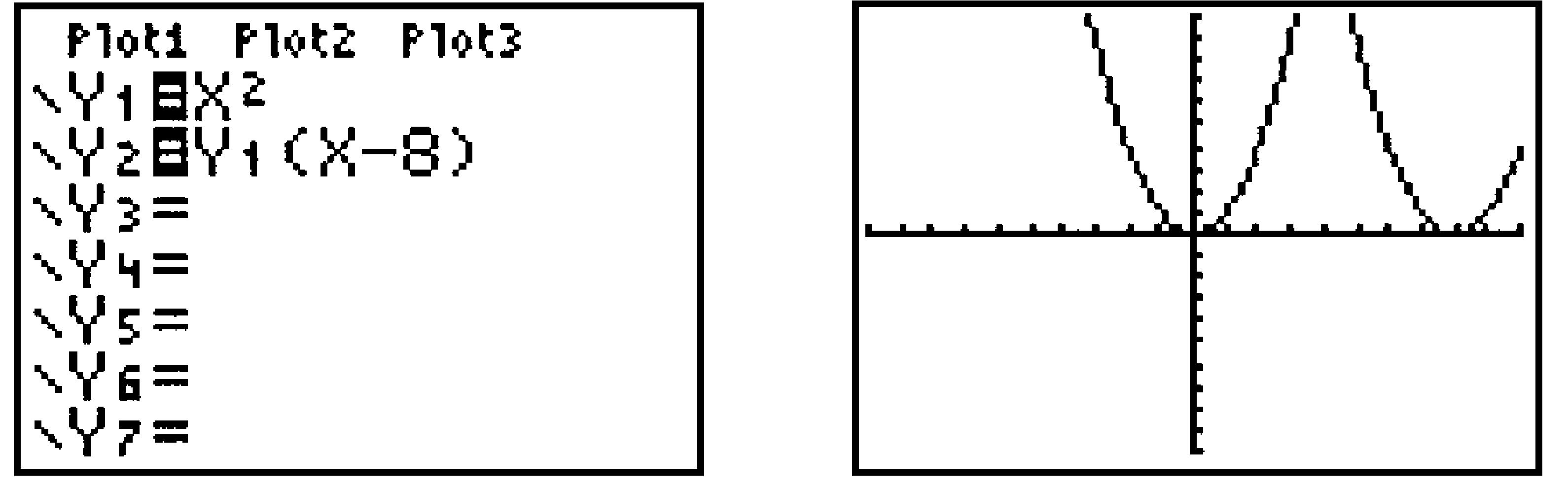
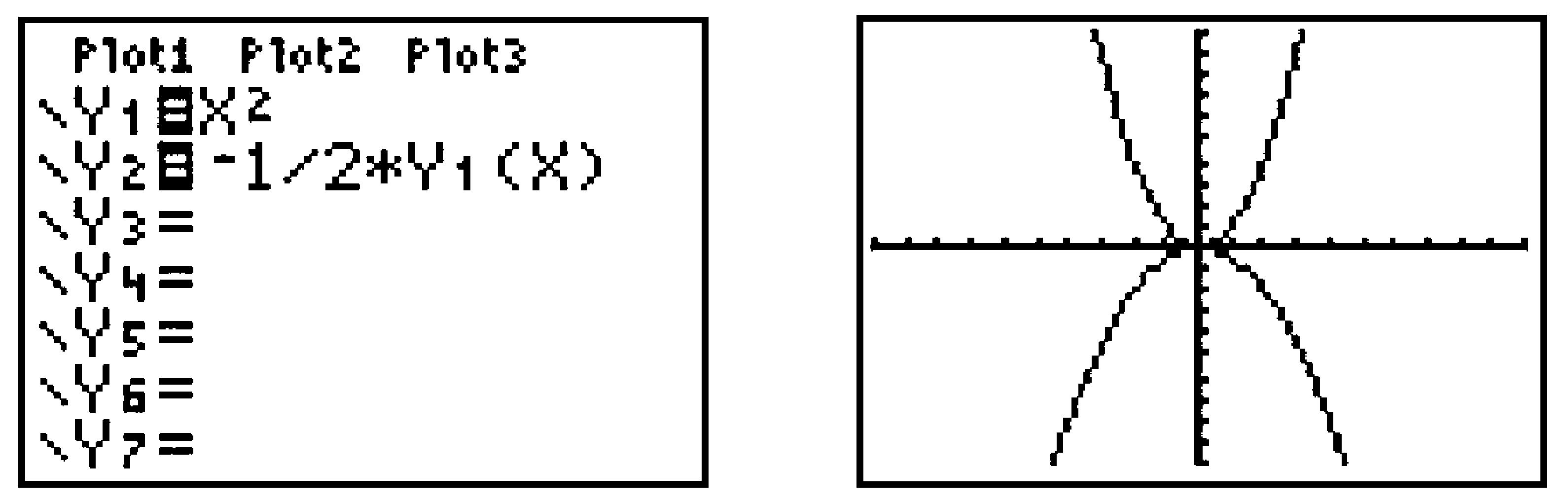
Skip to main content\(\require{cancel}\newcommand\degree[0]{^{\circ}}
\newcommand\Ccancel[2][black]{\renewcommand\CancelColor{\color{#1}}\cancel{#2}}
\newcommand{\alert}[1]{\boldsymbol{\color{magenta}{#1}}}
\newcommand{\blert}[1]{\boldsymbol{\color{blue}{#1}}}
\newcommand{\bluetext}[1]{\color{blue}{#1}}
\delimitershortfall-1sp
\newcommand\abs[1]{\left|#1\right|}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\newcommand{\fillinmath}[1]{\mathchoice{\underline{\displaystyle \phantom{\ \,#1\ \,}}}{\underline{\textstyle \phantom{\ \,#1\ \,}}}{\underline{\scriptstyle \phantom{\ \,#1\ \,}}}{\underline{\scriptscriptstyle\phantom{\ \,#1\ \,}}}}
\)