Section 1.1 Warm-Up
We begin by refreshing some basic skills for working with equations and graphs.
Subsection 1. Solve a linear equation
Recall that to solve an equation we want to "isolate" the variable on one side of the equals sign. We "undo" each operation performed on the variable by performing the opposite operation on both sides of the equation.
Subsubsection Examples
Example 1.1.
Solve the equation \(~~\dfrac{2}{3}x-5=7\)
Example 1.2.
Solve the equation \(~~2x+7=4x-3\)
Subsubsection Exercises
Checkpoint 1.3.
Solve the equation \(~~10=1-\dfrac{3x}{7}\)
Checkpoint 1.4.
Solve the equation \(~~6p-8=-3p-26\)
Checkpoint 1.5.
Solve the equation \(~~12=\dfrac{7u+4}{5}\)
Hint: Start by clearing the fraction: multiply both sides by 5.
Checkpoint 1.6.
Solve the equation \(~~0=13q+25-17q+7\)
Hint: Start by combining like terms.
Subsection 2. Solve a linear inequality
The rules for solving an inequality are the same as those for solving an equation, with one important difference:
Solving a Linear Inequality.
If we multiply or divide both sides by a negative number, we must reverse the direction of the inequality.
Subsubsection Examples
Example 1.7.
Solve \(~~-3x+1 \gt 7~~\) and graph the solutions on a number line.
The solutions are all the numbers less than \(-2\text{.}\) The graph of the solutions is shown below.

Example 1.8.
Solve \(~~-3 \lt 2x-5 \le 6~~\) and graph the solutions on a number line.
The solutions are all the numbers greater than 1 but less than 5.5. The graph of the solutions is shown below.
Recall that a solid dot on a number line indicates that the number is part of the solution; an open dot means that the number is not part of the solution.
Subsubsection Exercises
Checkpoint 1.9.
Solve the inequality \(~~8-4x \gt -2~~\) and graph the solutions on a number line.
\(x \lt \dfrac{5}{2}\)
Checkpoint 1.10.
Solve the inequality \(~~-6 \le \dfrac{4-x}{3} \lt 2~~\) and graph the solutions on a number line.
\(22 \ge x \gt -2\)
Checkpoint 1.11.
Solve the inequality \(~~3x-5 \lt -6x+7~~\) and graph the solutions on a number line.
\(x \lt \dfrac{4}{3}\)
Checkpoint 1.12.
Solve the inequality \(~~-6 \gt 4-5b \gt -21~~\) and graph the solutions on a number line.
\(2 \lt b \lt 5\)
Subsection 3. Verify a solution
We can always check a solution to an equation by verifying that it makes the equation true.
Subsubsection Examples
Example 1.13.
Verify that \(x=-5\) is a solution of the equation
We show that substituting \(-5\) for \(x\) makes the equation true. When we substitute a negative number for a variable, we should enclose the number in parentheses.
Because the expression does equal \(0\text{,}\) we see that \(x=-5\) is a solution.
Example 1.14.
Verify that \(x=-3\) is not a solution of the equation
We show that substituting \(-3\) for \(x\) does not make the equation true.
The left side of the equation does not equal 8 when \(x=-3\text{,}\) so \(x=-3\) is not a solution.
Subsubsection Exercises
Checkpoint 1.15.
Decide whether the given value is a solution of the equation.
Yes
Checkpoint 1.16.
Decide whether the given value is a solution of the equation.
No
Checkpoint 1.17.
Decide whether the given value is a solution of the equation.
Yes
Checkpoint 1.18.
Decide whether the given value is a solution of the equation.
No
Subsection 4. Solve an equation in two variables
A solution of an equation in two variables \(x\) and \(y\) is written as an ordered pair, \((x,y)\text{.}\) For example, the solution \((-2,5)\) means that \(x=-2\) and \(y=5\text{.}\)
Subsubsection Examples
Example 1.19.
Is \((-3,2)\) a solution of the equation \(~~x^2+4y^2=25\) ?
We substitute \(x=\alert{-3}\) and \(y=\alert{2}\) into the equation.
The ordered pair \((-3,2)\) satisfies the equation, so it is a solution.
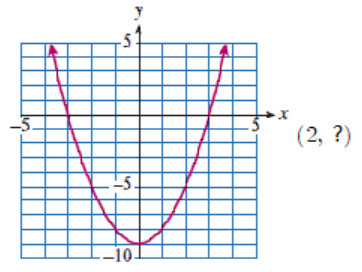
Example 1.20.
Which of the following ordered pairs are solutions of the equation whose graph is shown?
- \(\displaystyle (-3,-2)\)
- \(\displaystyle (-5,0)\)
- \(\displaystyle (1,-4)\)
- \(\displaystyle (-1,-6)\)
The graph of an equation is just a picture of its solutions, so points that lie on the graph are solutions of the equation.
The points \((-3,-2)\) and \((-1,-6)\) lie on the graph, so they represent solutions of the equation. The points \((-5,0)\) and \((1,-4)\) do not lie on the graph, so they are not solutions of the equation.
Subsubsection Exercises
Checkpoint 1.21.
Find a solution of the equation with the given coordinate.
Checkpoint 1.22.
Find a solution of the equation with the given coordinate.
Checkpoint 1.23.
Find a solution of the equation with the given coordinate.
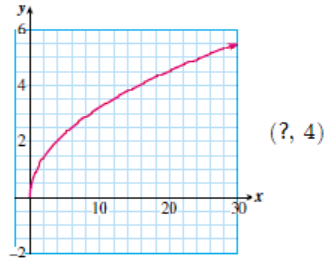
Checkpoint 1.24.
Find a solution of the equation with the given coordinate.