Trig Answers to Selected Exercises and Homework Problems

Appendix A Answers to Selected Exercises and Homework Problems

1 Triangles and Circles
1.1 Angles and Triangles
Homework 1.1

1.

Answer.

$isosceles triangle with vertex angle 30°$

3.

Answer.

$right triangle with legs 4 and 7$

5.

Answer.

$An isosceles triangle with one obtuse angle$

7.

Answer.

$\theta = 108.8\degree$

9.

Answer.

$\alpha = 29\degree$

11.

Answer.

$\beta = 77\degree$

13.

Answer.

$\alpha = 12\degree$

15.

Answer.

$\theta = 65\degree$

17.

Answer.

$\theta = 12\degree$

19.

Answer.

$\psi = 73\degree$

21.

Answer.

$\phi = 88\degree$

23.

Answer.

$\displaystyle \phi = 120\degree$
$\displaystyle \phi = 160\degree$
$\displaystyle \phi = \alpha + \beta$
An exterior angle is equal to the sum of the opposite interior angles.

25.

Answer.

$\theta = 72\degree, \phi = 54\degree$

27.

Answer.

$\theta = 100\degree, \phi = 30\degree$

29.

Answer.

$\displaystyle 180\degree$
$\displaystyle 90\degree$
a right triangle

31.

Answer.

They are base angles of an isosceles triangle.
They are base angles of an isosceles triangle.
$\angle OAB$ corresponds to $\theta$ of Problem 29, and $\angle OBC$ corresponds to $\phi$ of Problem 29.

33.

Answer.

$\alpha = 30\degree, \beta = 60\degree$

35.

Answer.

$x = 47\degree, y = 133\degree$

37.

Answer.

$x = 60\degree, y = 15\degree$

39.

Answer.

$x = 100\degree, y = 16\degree$

41.

Answer.

$x = 90\degree, y = 55\degree$

43.

Answer.

$x = 50\degree, y = 80\degree$

45.

Answer.

$\displaystyle \angle 1 = \angle 4, \angle 3 = \angle 5$
$\displaystyle 180\degree$
In the equation $\angle 4 + \angle 2 + \angle 5 = 180\degree,$ substitute $\angle 1$ for $\angle 4\text{,}$ and substitute $\angle 3$ for $\angle 5$ to conclude that the sum of the angles in the triangle is $180 \degree\text{.}$

47.

Answer.

$\angle 1 = 130\degree$ because vertical angles are equal. $\angle 2 = 50\degree$ because it makes a straight angle with a $130\degree$ angle. $\angle 3 = 65\degree$ because it is a base angle of an isosceles triangle whose vertex angle is $50\degree\text{.}$ $\angle 4 = 65\degree$ for the same reason. $\angle 5 = 25\degree$ because it is complementary to $\angle 4\text{.}$

1.2 Similar Triangles
Homework 1.2

1.

Answer.

$\triangle PQT \cong \triangle SRT\text{,}$ $x=7\text{,}$ $y=3, \alpha=18\degree$

3.

Answer.

$\triangle PRE \cong \triangle URN, z=12\text{,}$ $\theta = 10\degree\text{,}$ $\phi = 70\degree$

5.

Answer.

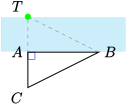
$\triangle ABT \cong \triangle ABC,$ so $AT=AC$

7.

Answer.

Similar. Corresponding sides are proportional.

9.

Answer.

Similar. Corresponding angles are equal.

11.

Answer.

$\angle A = 37\degree, \angle B = 37\degree$

13.

Answer.

$h = 12$

15.

Answer.

$p=35$

17.

Answer.

$g=84$

19.

Answer.

$h=30$

21.

Answer.

154 feet

23.

Answer.

1 mile

25.

Answer.

17.1 square feet

27.

Answer.

$y=\frac{12}{17}x$

29.

Answer.

$h=7.5$

31.

Answer.

$c=15$

33.

Answer.

$s=6$

35.

Answer.

$y=\frac{3}{5}x$

37.

Answer.

$y=5+\frac{3}{4}x$

39.

Answer.

$\angle B = 70\degree\text{,}$ $\angle CAD = 70\degree\text{,}$ $\angle DAB = 20\degree$
$\triangle DBA$ and $\triangle DAC.$ The hypotenuse is $BC$ in $\triangle ABC\text{,}$ $BA$ in $\triangle DBA\text{,}$ and $AC$ in $\triangle DAC\text{.}$ The short leg is $AB$ in $\triangle ABC\text{,}$ $DB$ in $\triangle DBA\text{,}$ and $DA$ in $\triangle DAC\text{.}$ The longer leg is $AC$ in $\triangle ABC\text{,}$ $DA$ in $\triangle DBA\text{,}$ and $DC$ in $\triangle DAC\text{.}$

1.3 Circles
Homework 1.3

1.

Answer.

13 miles

3.

Answer.

10, 10.00

5.

Answer.

$4\sqrt{5} \approx 8.94$

7.

Answer.

9.

Answer.

$2\sqrt {5}$

11.

Answer.

13.

Answer.

$triangle on grid$

$~~24.7$

15.

Answer.

$\displaystyle \sqrt{(x+3)^2+(y-4)^2}$
$\displaystyle \sqrt{(x+3)^2+(y-4)^2}=5$

17.

Answer.

The distance between the points $(x,y)$ and $(4,-1)$ is 3 units.

19.

Answer.

$6\sqrt{2}~$cm
8.49 cm

21.

Answer.

$25\pi~$sq in
78.54 sq in

23.

Answer.

approximation
approximation
approximation
exact

25.

Answer.

$x$	$-5$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$	$5$
$y$	$0$	$\pm 3$	$\pm 4$	$\pm \sqrt{21}$	$\pm 2\sqrt{6} $	$\pm 5$	$\pm 2\sqrt{6}$	$\pm \sqrt{21}$	$\pm 4$	$\pm 3 $	$0$

$circle on grid$

27.

Answer.

$circle on grid$
$\displaystyle x^2 + y^2 = 36$

29.

Answer.

$circle on grid$
$\displaystyle x^2 + y^2 \lt 9$

31.

Answer.

No real value of $y$ can satisfy $x^2 +y^2 = 16$ unless $-4 \le x \le 4$
The graph has no points where $x \gt 4$ and no points where $x \lt -4 $

33.

Answer.

$\sqrt{10}$

35.

Answer.

$\displaystyle 12\pi$

37.

Answer.

$circle$
$\displaystyle 4\pi$

39.

Answer.

$(-2\sqrt{5},-4), (2\sqrt{5},-4)$

$circle$

41.

Answer.

$P(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}), Q(\dfrac{1}{2}, \dfrac{-\sqrt{3}}{2}), R(\dfrac{-3}{4}, \dfrac{\sqrt{7}}{4}), S(\dfrac{-3}{4}, \dfrac{-\sqrt{7}}{4})$

43.

Answer.

$\displaystyle 45\degree$
$5\pi $ ft
$50\pi $ sq ft

45.

Answer.

$\displaystyle \dfrac{2}{5}$
$40\pi $ sq ft
$8\pi $ ft

47.

Answer.

$\displaystyle \dfrac{1}{10}$
$\dfrac{\pi}{10} $ sq km
$\dfrac{\pi}{5} $ km

49.

Answer.

$\displaystyle \dfrac{5}{6}$
$\dfrac{15\pi}{2}$ sq m
$5\pi $ m

51.

Answer.

2070 miles

53.

Answer.

54,000 miles
2240 mph

55.

Answer.

$\displaystyle (x-3)^2 + (y+2)^2 = 36$
$\displaystyle (x-h)^2 + (y-k)^2 = r^2$

1.4 Chapter 1 Summary and Review
Chapter 1 Review Problems

1.

Answer.

$triangle$

3.

Answer.

$triangle$

5.

Answer.

$\alpha = \beta = \gamma = 60\degree$

7.

Answer.

$\phi = \omega = 79\degree$

9.

Answer.

$\theta = 65\degree\text{,}$ $\phi = 25\degree$

11.

Answer.

$\delta = 30\degree\text{,}$ $\gamma = 60\degree$

13.

Answer.

$\sigma = 39\degree\text{,}$ $\omega = 79\degree$

15.

Answer.

$\alpha = 51\frac{3}{7}\degree\text{,}$ $\beta = 64\frac{2}{7}\degree$

17.

Answer.

$\triangle ABC \cong \triangle EDC\text{,}$ $\alpha = 40\degree\text{,}$ $\beta = 130\degree\text{,}$ $x=32$

19.

Answer.

Yes, three pairs of equal angles

21.

Answer.

Yes, three pairs of equal angles

23.

Answer.

25.

Answer.

27.

Answer.

$y=\dfrac{5x}{2}$

29.

Answer.

$y=\dfrac{7x}{3}$

31.

Answer.

$y=\dfrac{x}{3}$

33.

Answer.

$y=\dfrac{12x}{5}$

35.

Answer.

$\alpha=70\degree$

37.

Answer.

14 ft

39.

Answer.

$3\frac{3}{4}$ in

41.

Answer.

All side have length $\sqrt{61},$ opposite sides have slopes $\dfrac{5}{6}$ and $\dfrac{-6}{5}$

43.

Answer.

$AC=BC=18$

45.

Answer.

$\displaystyle \sqrt{(x-2)^2+(y-5)^2}=3$
$\displaystyle (x-2)^2+(y-5)^2=9$

47.

Answer.

$4\sqrt{5} \approx 8.944$ cm

49.

Answer.

$(\dfrac{-1}{3}, \dfrac{2\sqrt{2}}{3}), (\dfrac{-1}{3}, \dfrac{-2\sqrt{2}}{3})$

51.

Answer.

$4\pi$ ft
$\displaystyle 20\pi~ \text{ft}^2$

53.

Answer.

$\displaystyle 45\degree, 60\degree$
$\dfrac{49\pi}{8}~ \text{in}^2, 6\pi~ \text{in}^2$ Delbert
$\dfrac{79\pi}{4}$ in, $2\pi$ in, Francine

2 The Trigonometric Ratios
2.1 Side and Angle Relationships
Homework 2.1

1.

Answer.

The sum of the angles is not $180\degree\text{.}$

3.

Answer.

The exterior angle is not equal to the sum of the opposite interior angles.

5.

Answer.

The sum of the acute angles is not $90\degree\text{.}$

7.

Answer.

The largest side is not opposite the largest angle.

9.

Answer.

The Pythagorean theorem is not satisfied.

11.

Answer.

$5^2 + 12^2 = 13^2\text{,}$ but the angle opposite the side of length 13 is $85\degree\text{.}$

13.

Answer.

$4 \lt x \lt 16$

15.

Answer.

$0 \lt x \lt 16$

17.

Answer.

21 in

19.

Answer.

$6\sqrt{2}~$in

21.

Answer.

The rectangle is $6\sqrt{10}$ inches by $18\sqrt{10}$ inches.

23.

Answer.

25.

Answer.

$\sqrt{3}$

27.

Answer.

29.

Answer.

Yes

31.

Answer.

33.

Answer.

The distance from $(0,0)$ to $(3,3)$ is $3\sqrt{2}\text{,}$ and the distance from $(3,3)$ to $(6,0)$ is also $3\sqrt{2}\text{,}$ so the triangle is isosceles. The distance from $(0,0)$ to $(6,0)$ is 6, and $(3\sqrt{2})^2 + (3\sqrt{2})^2 = 6^2$ so the triangle is a right triangle.

35.

Answer.

25 ft

37.

Answer.

$\alpha=30\degree, \beta=60\degree, h=\sqrt{3}$

39.

Answer.

$8\sqrt{3}$ in

41.

Answer.

43.

Answer.

$(-1,0)$ and $(1,0)\text{;}$ 2
$\sqrt{(p+1)^2+q^2}$ and $\sqrt{(p-1)^2+q^2}$
\begin{align*} (\sqrt{(p+1)^2+q^2})^2 \amp + (\sqrt{(p-1)^2+q^2})^2\\ \amp = p^2+2p+1+q^2+p^2-2p+1+q^2\\ \amp =2p^2+2+2q^2=2+2(p^2+q^2)\\ \amp =2+2(1)=4 \end{align*}

2.2 Right Triangle Trigonometry
Homework 2.2

1.

Answer.

0.91
0.91
0.9063

3.

Answer.

0.77
0.77
0.7660

5.

Answer.

$\displaystyle 4\sqrt{13} \approx 14.42$
$\sin\theta = 0.5547\text{,}$ $\cos\theta = 0.8321\text{,}$ $\tan\theta = 0.6667$

7.

Answer.

$\displaystyle 4\sqrt{15} \approx 15.49$
$\sin(\theta) = 0.9682\text{,}$ $\cos(\theta) = 0.2500\text{,}$ $\tan(\theta) = 3.8730$

9.

Answer.

$\displaystyle 2\sqrt{67} \approx 16.37$
$\sin(\theta) = 0.2116\text{,}$ $\cos(\theta) = 0.9774\text{,}$ $\tan(\theta) = 0.2165$

11.

Answer.

$triangles$

(Answers may vary)

13.

Answer.

$triangles$

(Answers may vary)

15.

Answer.

$triangles$

(Answers may vary)

17.

Answer.

14.41

19.

Answer.

37.86

21.

Answer.

86.08

23.

Answer.

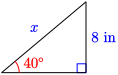
25.

Answer.

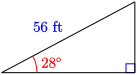
27.

Answer.

$triangle$
$\tan(54.8\degree) = \dfrac{h}{20}\text{,}$ 170.1 yd

29.

Answer.

$triangle$
$\tan(36.2\degree) = \dfrac{260}{d}\text{,}$ 355.2 ft

31.

Answer.

$triangle$
$\sin(48\degree) = \dfrac{a}{1500}\text{,}$ 1114.7 m

33.

Answer.

$triangle$
$\cos(38\degree) = \dfrac{1800}{x}\text{,}$ 2284.2 m

35.

Answer.

$x=\dfrac{82}{\tan(\theta)}$

37.

Answer.

$x=11~\sin(\theta)$

39.

Answer.

$x=\dfrac{9}{cos(\theta})$

41.

Answer.

$36 ~\sin(25\degree) \approx 15.21$

43.

Answer.

$46~ \sin(20\degree) \approx 15.73$

45.

Answer.

$12~ \sin(40\degree) \approx 7.71$

47.

Answer.

$~~~~$	sin(\theta)	cos(\theta)	tan(\theta)
$\theta$	$\frac{3}{5}$	$\frac{4}{5}$	$\frac{3}{4}$
$\phi$	$\frac{4}{5}$	$\frac{3}{5}$	$\frac{4}{3}$

49.

Answer.

$~~~~$	sin(\theta)	cos(\theta)	tan(\theta)
$\theta$	$\frac{1}{\sqrt{5}}$	$\frac{2}{\sqrt{5}}$	$\frac{1}{2}$
$\phi$	$\frac{2}{\sqrt{5}}$	$\frac{1}{\sqrt{5}}$	$2$

51.

Answer.

$\theta$ and $\phi$ are complements.
$\sin(\theta) = \cos(\phi)$ and $\cos(\theta) = \sin(\phi)\text{.}$ The side opposite $\theta $ is the side adjacent to $\phi\text{,}$ and vice versa.

53.

Answer.

As $\theta$ increases, $\tan(\theta)$ increases also. The side opposite $\theta$ increases in length while the side adjacent to $\theta$ remains fixed.
As $\theta$ increases, $\cos (\theta)$ decreases. The side adjacent to $\theta$ remains fixed while the hypotenuse increases in length.

55.

Answer.

As $\theta$ decreases toward $0\degree\text{,}$ the side opposite $\theta$ approaches a length of 0, so sin $(\theta)$ approaches 0. But as $\theta$ increases toward $90\degree\text{,}$ the length of the side opposite $\theta$ approaches the length of the hypotenuse, so $\sin(\theta)$ approaches 1.

57.

Answer.

The triangle is not a right tringle.

59.

Answer.

$\dfrac{21}{20}$ is the ratio of hypotenuse to the adjacent side, which is the reciprocal of $\cos(\theta)\text{.}$

61.

Answer.

0.2358
sine
$\displaystyle 48\degree$
$\displaystyle 77\degree$

63.

Answer.

$\displaystyle \dfrac{5}{12}$
$\displaystyle 3$
$\displaystyle \dfrac{2}{3}$
$\displaystyle \dfrac{2}{\sqrt{7}}$

65.

Answer.

Although the triangles may differ in size, the ratio of the side adjacent to the angle to the hypotenuse of the triangle remains the same because the triangles would all be similar, and hence corresponding sides are proportional.

67.

Answer.

$\displaystyle \dfrac{2}{3}$
$\displaystyle \dfrac{2}{3}$
$triangle$

2.3 Solving Right Triangles
Homework 2.3

1.

Answer.

$A=61\degree, ~a=25.26,~ c=28.88$

3.

Answer.

$A=68\degree, ~a=0.93,~ b=0.37$

5.

Answer.

$triangle$
$B=48\degree\text{,}$ $~a=17.4\text{,}$ $~ b=19.3$

7.

Answer.

$triangle$
$A=57\degree\text{,}$ $~b=194.4\text{,}$ $~ c=357.7$

9.

Answer.

$triangle$
$B=78\degree\text{,}$ $~b=18.8\text{,}$ $~ c=19.2$

11.

Answer.

$triangle$
- Solve $\sin (53.7\degree) = \dfrac{8.2}{c}$ for $c\text{.}$
- Solve $\tan (53.7\degree) = \dfrac{8.2}{a}$ for $a\text{.}$
- Subtract $53.7\degree$ from $90\degree$ to find $A\text{.}$

13.

Answer.

$triangle$
- Solve $\cos (25\degree) = \dfrac{40}{c}$ for $c\text{.}$
- Solve $\tan (25\degree) = \dfrac{a}{40}$ for $a\text{.}$
- Subtract $25\degree$ from $90\degree$ to find $B\text{.}$

15.

Answer.

$triangle$
- Solve $\sin (64.5\degree) = \dfrac{a}{24}$ for $a\text{.}$
- Solve $\cos (64.5\degree) = \dfrac{b}{24}$ for $b\text{.}$
- Subtract $64.5\degree$ from $90\degree$ to find $B\text{.}$

17.

Answer.

$74.2\degree$

19.

Answer.

$56.4\degree$

21.

Answer.

$66.0\degree$

23.

Answer.

$11.5\degree$

$triangle$

25.

Answer.

$56.3\degree$

$triangle$

27.

Answer.

$73.5\degree$

$triangle$

29.

Answer.

$\cos (15\degree) = 0.9659~$ and $~\cos^{-1} (0.9659) = 15\degree$

31.

Answer.

$\tan (65\degree) = 2.1445~$ and $~\tan^{-1} (2.1445) = 65\degree$

33.

Answer.

$\sin^{-1}(0.6) \approx 36.87\degree$ is the angle whose sine is $0.6\text{.}$ $(\sin 6\degree)^{-1} \approx 9.5668$ is the reciprocal of $\sin (6\degree)\text{.}$

35.

Answer.

$triangle$
$\displaystyle \sin (\theta) = \dfrac{1806}{3(2458)},~14.6\degree$

37.

Answer.

$triangle$
$\displaystyle \tan \theta = \dfrac{32}{10},~72.6\degree$

39.

Answer.

$triangle$
$c = 10\sqrt{10} \approx 31.6\text{,}$ $~ A \approx 34.7\degree\text{,}$ $~ B \approx 55.3\degree$

41.

Answer.

$triangle$
$a = \sqrt{256.28} \approx 16.0\text{,}$ $~ A \approx 56.5\degree\text{,}$ $~ B \approx 33.5\degree$

43.

Answer.

$triangle$
$\tan^{-1}(\dfrac{26}{30}) \approx 40.9\degree,~~91\sqrt{1676} \approx 3612.6$ cm

45.

Answer.

$triangle$
$6415$ km

47.

Answer.

$triangle$
$462.9$ ft

49.

Answer.

(a) and (b)

51.

Answer.

(a) and (d)

53.

Answer.

$\dfrac{\sqrt{3}}{2} \approx 0.8660$

55.

Answer.

$\dfrac{1}{\sqrt{3}} =\dfrac{\sqrt{3}}{3} \approx 0.5774$

57.

Answer.

$1.0000$

59.

Answer.

$\theta$	$~~~0\degree~~~$	$~~~30\degree~~~$	$~~~45\degree~~~$	$~~~60\degree~~~$	$~~~90\degree~~~$
$\sin (\theta)$	$0$	$\dfrac{1}{2} $	$\dfrac{\sqrt{2}}{2} $	$\dfrac{\sqrt{3}}{2} $	$1$
$\cos (\theta)$	$1$	$\dfrac{\sqrt{3}}{2} $	$\dfrac{\sqrt{2}}{2} $	$\dfrac{1}{2} $	$0$
$\tan (\theta)$	$0$	$\dfrac{1}{\sqrt{3}} $	$1$	$\sqrt{3}$	undefined

61.

Answer.

smaller
larger
larger

63.

Answer.

$a = 3\sqrt{3},~b = 3,~B = 30\degree$

65.

Answer.

$a = b = 4\sqrt{2},~B = 45\degree$

67.

Answer.

$e = 4,~f = 4\sqrt{3},~F = 120\degree$

69.

Answer.

$d = 2\sqrt{3},~e = 2\sqrt{2}, f = \sqrt{2} + \sqrt{6}, ~F = 75\degree$

71.

Answer.

$a = 20,~b = 20,~c = 20\sqrt{2}$

73.

Answer.

$32\sqrt{3}$ cm
$128\sqrt{3}$ sq cm

75.

Answer.

$10$ sq cm
$10\sqrt{2}$ sq cm
$10\sqrt{3}$ sq cm

77.

Answer.

$64$ sq in
$4\sqrt{2}$ by $4\sqrt{2}\text{,}$ area $32$ sq in
$\displaystyle 2:1$

2.4 Chapter 2 Summary and Review
Chapter 2 Review Problems

1.

Answer.

If $C \gt 93\degree\text{,}$ then $A+B+C \gt 180\degree$

3.

Answer.

If $A \lt B \lt 58\degree\text{,}$ then $A+B+C \lt 180\degree$

5.

Answer.

If $C \gt 50\degree\text{,}$ then $A+B+C \gt 180\degree$

7.

Answer.

$triangle$

9.

Answer.

$a = 97$

11.

Answer.

$c = 52$

13.

Answer.

Yes

15.

Answer.

$\theta = 35.26\degree$

17.

Answer.

No. $a = 6,~ c = 10$ or $a = 9,~ c = 15$

19.

Answer.

$\displaystyle w = 86.05$
$\displaystyle \sin (\theta) = 0.7786,~ \cos(\theta) = 0.6275, ~ \tan (\theta) = 1.2407$

21.

Answer.

$\displaystyle y = 16.52$
$\displaystyle \sin (\theta) = 0.6957,~ \cos (\theta) = 0.7184, ~ \tan (\theta) = 0.9684$

23.

Answer.

$a = 7.89$

25.

Answer.

$x = 3.57$

27.

Answer.

$b = 156.95$

29.

Answer.

$A = 30\degree,~ a = \dfrac{23\sqrt{3}}{3},~ c = \dfrac{46\sqrt{3}}{3} $

31.

Answer.

$F = 105\degree,~ d = 10\sqrt{2},~ e = 20,~ f = 10 + 10\sqrt{3} $

33.

Answer.

$3$ cm

35.

Answer.

$43.30$ cm

37.

Answer.

$15.92$ m

39.

Answer.

$114.02$ ft, $37.87\degree$

41.

Answer.

$\displaystyle 60.26\degree$
$\displaystyle 60.26\degree$
$\displaystyle m = \dfrac{7}{4} = \tan(\theta)$

43.

Answer.

$\displaystyle c^2$
$\displaystyle b - a,~ (b - a)^2$
$\displaystyle \dfrac{1}{2}ab$
$\displaystyle 4(\dfrac{1}{2}ab) + (a - b)^2 = 2ab + b^2 - 2ab + a^2 = a^2 + b^2$

3 Laws of Sines and Cosines
3.1 Obtuse Angles
Homework 3.1

1.

Answer.

$\displaystyle 150\degree$
$\displaystyle 135\degree$
$\displaystyle 60\degree$
$\displaystyle 155\degree$
$\displaystyle 15\degree$
$\displaystyle 70\degree$

3.

Answer.

$\displaystyle (5,2)$
$\displaystyle \sqrt{29}$
$\displaystyle \cos (\theta) = \dfrac{5}{\sqrt{29}},~~\sin (\theta) = \dfrac{2}{\sqrt{29}},~~\tan (\theta) = \dfrac{2}{5}$

5.

Answer.

$\displaystyle (-4,7)$
$\displaystyle \sqrt{65}$
$\displaystyle \cos (\theta) = \dfrac{-4}{\sqrt{65}},~~\sin (\theta) = \dfrac{7}{\sqrt{65}},~~\tan (\theta) = \dfrac{-7}{4}$

7.

Answer.

$\sin (\theta) = \dfrac{9}{\sqrt{97}}\text{,}$ $~\cos (\theta) = \dfrac{4}{\sqrt{97}}$
$angle$
$\sin (180\degree - \theta) = \dfrac{9}{\sqrt{97}}\text{,}$ $~\cos (180\degree - \theta) = \dfrac{-4}{\sqrt{97}}$
$\displaystyle \theta = 66\degree,~~180\degree - \theta = 114\degree$

9.

Answer.

$\sin (\theta) = \dfrac{8}{\sqrt{89}}\text{,}$ $~\cos (\theta) = \dfrac{-5}{\sqrt{89}}$
$angle$
$\sin (180\degree - \theta) = \dfrac{8}{\sqrt{89}}\text{,}$ $~\cos (180\degree - \theta) = \dfrac{5}{\sqrt{89}}$
$\displaystyle \theta = 122\degree,~~180\degree - \theta = 58\degree$

11.

Answer.

$angle$
$\cos (\theta) = \dfrac{-5}{13}\text{,}$ $~\sin (\theta) = \dfrac{12}{13}\text{,}$ $~\tan (\theta) = \dfrac{-12}{5}$
$\displaystyle 112.6\degree$

13.

Answer.

$angle$
$\displaystyle \cos (\theta) = \dfrac{3}{5},~~\tan (\theta) = \dfrac{-3}{4}$
$\displaystyle 143.1\degree$

15.

Answer.

$angle$
$\sin (\theta) = \dfrac{\sqrt{112}}{11}\text{,}$ $~\tan (\theta) = \dfrac{\sqrt{112}}{3}$
$\displaystyle 74.2\degree$

17.

Answer.

$angle$
$\sin (\theta) = \dfrac{1}{\sqrt{37}}\text{,}$ $~\cos (\theta) = \dfrac{-6}{\sqrt{37}}$
$\displaystyle 170.5\degree$

19.

Answer.

$angle$
$\sin (\theta) = \dfrac{4}{\sqrt{17}}\text{,}$ $~\cos (\theta) = \dfrac{1}{\sqrt{17}}$
$\displaystyle 76.0\degree$

21.

Answer.

$\theta$	$~~~0\degree~~~$	$~~~30\degree~~~$	$~~~45\degree~~~$	$~~~60\degree~~~$	$~~~90\degree~~~$	$~~~120\degree~~~$	$~~~135\degree~~~$	$~~~150\degree~~~$	$~~~180\degree~~~$
$\cos (\theta)$	$1$	$\dfrac{\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{2}$	$0$	$\dfrac{-1}{2}$	$\dfrac{1}{\sqrt{2}}~$	$\dfrac{-\sqrt{3}}{2}$	$-1$
$\sin (\theta)$	$0$	$\dfrac{1}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{\sqrt{3}}{2}$	$1$	$\dfrac{\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{2}$	$0$
$\tan (\theta)$	$0$	$\dfrac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$	$\text{undefined}$	$-\sqrt{3}$	$-1$	$\dfrac{-1}{\sqrt{3}}$	$0$

23.

Answer.

$\displaystyle \sin (\theta) = \sin (180\degree - \theta)$
$\displaystyle \cos (\theta) = -\cos (180\degree - \theta)$
$\displaystyle \tan (\theta) = -\tan (180\degree - \theta)$

25.

Answer.

$\displaystyle \theta \approx 41.4\degree,~~\phi \approx 138.6\degree$
$angles$
$\displaystyle \sin (\theta) = \sin (\phi) = \dfrac{\sqrt{7}}{4}$

27.

Answer.

$\displaystyle \theta \approx 81.2\degree,~~\phi \approx 98.8\degree$
$angles$
$\displaystyle \sin (\theta) = \sin (\phi) = \dfrac{\sqrt{156279}}{400} \approx 0.9883$

29.

Answer.

$44.4\degree$ and $135.6\degree$

31.

Answer.

$57.1\degree$ and $122.9\degree$

33.

Answer.

$41.8\degree$ and $138.2\degree$

35.

Answer.

$\sin (123\degree) = q\text{,}$ $~\cos (33\degree) = q\text{,}$ $~\cos (147\degree) = -q$

37.

Answer.

$\cos (106\degree) = -m\text{,}$ $~\sin (16\degree) = m\text{,}$ $~\sin (164\degree) = m$

39.

Answer.

$angles$
$\displaystyle (4,3),~ (8,6)$
$\displaystyle y = \tan^{-1}\left(\dfrac{3}{4}\right) \approx 36.87\degree$
$angles$

$\displaystyle (-4,3),~ (-8,6);~ 143.13\degree$

41.

Answer.

$b=8$ in, $h=3\sqrt{3}$ in
$12\sqrt{3}$ sq in

43.

Answer.

$b=6-\dfrac{3\sqrt{2}}{2}$ mi, $h=\dfrac{3\sqrt{2}}{2}$ mi
$\dfrac {18\sqrt{2} - 9}{4}$ sq mi

45.

Answer.

$angle$

$\displaystyle (-1, \sqrt{3})$
$\displaystyle (-\sqrt{3}, 3)$

47.

Answer.

$triangle$

$\displaystyle (-3,3)$
$\displaystyle (-\sqrt{5}, \sqrt{5})$

49.

Answer.

$20.71$ sq m

51.

Answer.

$55.51$ sq cm

55.

Answer.

$38.04$ sq units

57.

Answer.

$13,851.3$ sq ft

59.

Answer.

$\displaystyle (-74.97, 59.00)$
$\displaystyle BC = 141.97,~~PC = 59.00$
$\displaystyle 153.74$

61.

Answer.

$\dfrac{\sqrt{5} - 1}{4}$

63.

Answer.

Bob found an acute angle. The obtuse angle is the supplement of $17.46\degree\text{,}$ or $162.54\degree\text{.}$

65.

Answer.

$triangle$
$\cos (\theta) = \dfrac{x}{3}\text{,}$ $~\sin (\theta) = \dfrac{\sqrt{9 - x^2}}{3}\text{,}$ $~\tan (\theta) = \dfrac{\sqrt{9 - x^2}}{x}$

67.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-\sqrt{4 - y^2}}{2}\text{,}$ $~\sin (\theta) = \dfrac{y}{2}\text{,}$ $~\tan (\theta) = \dfrac{-y}{\sqrt{4 - y^2}}$

69.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-1}{\sqrt{1+ m^2}}\text{,}$ $~\sin (\theta) = \dfrac{-m}{\sqrt{1+ m^2}}\text{,}$ $~\tan (\theta) = m$

3.2 The Law of Sines
Homework 3.2

1.

Answer.

$x = 7.85$

3.

Answer.

$q = 33.81$

5.

Answer.

$d = 28.37$

7.

Answer.

$\theta = 30.80\degree$

9.

Answer.

$\theta = 126.59\degree$

11.

Answer.

$\beta = 37.14\degree$

13.

Answer.

$triangle$

$a = 4.09\text{,}$ $~c = 9.48\text{,}$ $~C = 115\degree$

15.

Answer.

$triangle$

$b = 2.98\text{,}$ $~A = 36.54\degree\text{,}$ $~B = 99.46\degree$

17.

Answer.

$triangle$

$a = 43.55\text{,}$ $~b = 54.62\text{,}$ $~C = 99\degree$

19.

Answer.

$triangle$

b. 808.1 ft

21.

Answer.

$triangle$

b. 68.2 km

23.

Answer.

$triangle$

b.1.23 mi $+$ 0.99 mi; 0.22 mi

25.

Answer.

$triangle$

b. 322.6 m

27.

Answer.

$\displaystyle 1\degree$
$\displaystyle 66\degree$
2617.2 ft
1022.6 ft

29.

Answer.

540,000 AU $\approx 8.1\times 10^{13}$ km

31.

Answer.

750,000 AU $\approx 1.1\times 10^{14}$ km

33.

Answer.

$\displaystyle \dfrac{3}{2}$
No, $a$ is too short.
2
1

35.

Answer.

1,

$triangle$
0,

$triangle$
2,

$triangle$
1,

$triangle$

37.

Answer.

$\displaystyle C = 25.37\degree,~B = 114.63\degree,~ b = 16.97$
$C =58.99\degree,~B = 81.01\degree,~ b = 9.22$ or $C = 121.01\degree,~B = 18.99\degree,~ b = 3.04$
no solution
5.14

39.

Answer.

$A = 40.44\degree,~B = 114.56\degree$ or $A = 139.56\degree,~B = 15.44\degree$

41.

Answer.

$C = 37.14\degree,~A = 93.86\degree$

43.

Answer.

1299 yd or 277.2 yd

45.

Answer.

11.79
24.16
24.16

47.

Answer.

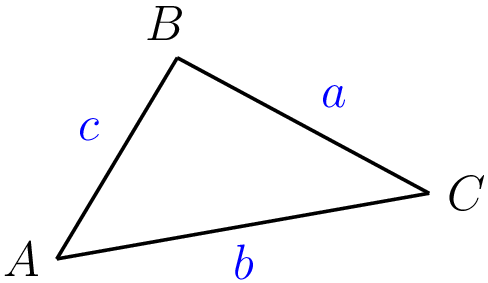
$\displaystyle \dfrac{1}{2} ab \sin (C)$
$\displaystyle \dfrac{1}{2} ac \sin (B)$
$\displaystyle \dfrac{1}{2} bc \sin (A)$

49.

Answer.

$triangle$
$\displaystyle b = \dfrac{h}{\sin (A)}$
$\displaystyle h = a \sin (B)$
$\displaystyle b = \dfrac{a \sin (B)}{\sin (A)} $
ii

3.3 The Law of Cosines
Homework 3.3

1.

Answer.

$\displaystyle 74 - 70\cos (\theta)$
12.78
135.22

3.

Answer.

$\displaystyle \dfrac{a^2 + c^2 - b^2}{2ac}$
$\displaystyle -0.4$

5.

Answer.

$\displaystyle b^2 - 8 \cos (\alpha)b - 65 = 0$
$\displaystyle 11.17,~ -5.82$

7.

Answer.

7.70

9.

Answer.

13.44

11.

Answer.

5.12

13.

Answer.

$133.43\degree$

15.

Answer.

$40.64\degree$

17.

Answer.

$A = 91.02\degree,~B = 37.49\degree,~C = 51.49\degree$

19.

Answer.

$A = 34.34\degree,~B = 103.49\degree,~C = 42.17\degree$

21.

Answer.

6.30 or 2.70

23.

Answer.

29.76 or 5.91

25.

Answer.

16.00

27.

Answer.

Law of Cosines: $61^2 = 29^2 + 46^2 - 2\cdot 29 \cdot 46 \cos (\phi)$

29.

Answer.

Law of Sines: $\dfrac{a}{\sin (46\degree)} = \dfrac{16}{\sin (25\degree)}$

31.

Answer.

First the Law of Cosines: $x^2 = 47^2 + 29^2 - 2 \cdot 47 \cdot 29 \cos (81\degree)\text{,}$ then either the Law of Sines: $\dfrac{\sin (\theta)}{47} = \dfrac{\sin (81\degree)}{x}$ or the Law of Cosines: $47^2 = x^2 + 29^2 - 2 \cdot x \cdot 29\cos (\theta)$

33.

Answer.

Law of Cosines: $9^2 = 4^2 + z^2 - 2\cdot 4 \cdot z \cos (28\degree)\text{,}$ or use the Law of Sines first to find the (acute) angle opposite the side of length 4, then find the angle opposite the side of length $z$ by subtracting the sum of the known angles from $180\degree\text{,}$ then using the Law of Sines again.

35.

Answer.

$triangle$
$b = 16.87\text{,}$ $~ A = 85.53\degree\text{,}$ $~C = 47.47\degree$

37.

Answer.

$triangle$
$A = 58.41\degree\text{,}$ $B = 48.19\degree\text{,}$ $C = 73.40\degree$

39.

Answer.

$triangle$
$a = 116.52\text{,}$ $~ A = 85.07\degree\text{,}$ $~C = 56.93\degree$ or $a = 37.93\text{,}$ $~ A = 18.93\degree\text{,}$ $~C = 123.07\degree$

41.

Answer.

$triangle$
$a = 7.76\text{,}$ $~ b = 8.97\text{,}$ $~C = 39\degree$

43.

Answer.

$triangle$
1383.3 m

45.

Answer.

$triangle$
2123 mi, $168.43\degree$ east of north

47.

Answer.

$triangle$
$7.74\degree$ west of south, 917.9 mi

49.

Answer.

$triangle$
92.99 ft

51.

Answer.

$147.73~ \text{cm}^2$

53.

Answer.

10.53

55.

Answer.

4.08

57.

Answer.

First figure: $b - x$ is the base of the small right triangle. Second: $-x$ is the horizontal distance between $P$ and the $x$-axis, so $b + (-x)$ or $b - x$ is the base of the large right triangle. Third: $x = 0\text{,}$ and $b$ is the base of a right triangle.
First: $x$ and $y$ are the legs of a right triangle, $a$ is the hypotenuse. Second: $-x$ and $y$ are the legs of a right triangle with hypotenuse $a\text{.}$ Third: $x = 0$ and $y = a$
$\displaystyle x = a \cos (C)$

59.

Answer.

\begin{align*} b^2 + c^2 \amp = (a^2 + c^2 - 2ac \cos (B)) + (a^2 + b^2 - 2bc \cos (C))\\ \amp = 2a^2 + b^2 + c^2 - 2a(c \cos (B) + b \cos (C)) \end{align*}

so $2a^2 = 2a(c \cos (B) + b \cos (C))\text{,}$ and dividing both sides by $2a$ yields $a = (c \cos (B) + b \cos (C)$

61.

Answer.

For the first equation, start with the Law of Cosines in the form

\begin{equation*} a^2 = b^2 + c^2 - 2bc \cos (A) \end{equation*}

Add $2ab + 2bc \cos (A) - a^2$ to both sides of the equation, factor the right side, then divide both sides by $2bc\text{.}$

For the second equation, start with the Law of Cosines in the form

\begin{equation*} b^2 + c^2 - 2bc \cos (A) = a^2 \end{equation*}

Add $2bc - b^2 - c^2$ to both sides of the equation, factor the right side, then divide both sides by $2bc\text{.}$

3.4 Chapter 3 Summary and Review
Chapter 3 Review Problems

1.

Answer.

$\dfrac{1}{2},~\dfrac{\pm\sqrt{3}}{2}$

3.

Answer.

$triangle$
49.33
$triangle$

$\displaystyle 114\degree$

5.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-2}{\sqrt{13}}\text{,}$ $~\sin (\theta) = \dfrac{3}{\sqrt{13}}\text{,}$ $~\tan (\theta)= \dfrac{-3}{2} $
$\displaystyle \theta = 123.7\degree$

7.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-4}{5}\text{,}$ $~\sin (\theta) = \dfrac{3}{5}\text{,}$ $~\tan (\theta) = \dfrac{-3}{4} $
$\displaystyle \theta = 143.1\degree$

9.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-\sqrt{11}}{6}\text{,}$ $~\sin (\theta) = \dfrac{5}{6}\text{,}$ $~\tan (\theta) = \dfrac{-5}{\sqrt{11}} $
$\displaystyle \theta = 123.6\degree$

11.

Answer.

$triangle$
$\cos (\theta) = \dfrac{-7}{25}\text{,}$ $~\sin (\theta) = \dfrac{24}{25}\text{,}$ $~\tan (\theta) = \dfrac{-24}{7} $
$\displaystyle \theta = 106.3\degree$

13.

Answer.

$9.9\degree\text{,}$ $~ 170.1\degree$

15.

Answer.

$22.0\degree,~ 158.0\degree$

17.

Answer.

$\displaystyle 7\sqrt{2}$
$\displaystyle 28\sqrt{2}$

19.

Answer.

5127.39 sq ft

21.

Answer.

$20.41\degree$

23.

Answer.

$a = 27.86$

25.

Answer.

$b = 6.03$

27.

Answer.

$w = 62.10$

29.

Answer.

$s = 15.61~ \text{or}~ 57.45$

31.

Answer.

$triangle$
8.82

33.

Answer.

$triangle$
$\displaystyle 32.57\degree$

35.

Answer.

$triangle$
16.29

37.

Answer.

$triangle$
$\displaystyle 58.65\degree$

39.

Answer.

$triangle$
17.40

$triangle$
80.93

41.

Answer.

$triangle$
16.08 mi, 80.4 mph

43.

Answer.

$triangle Francine-Delbert-Tree$
72.47

45.

Answer.

$triangle Giselle-Hakim-blimp$

353.32
217.52 m

47.

Answer.

79.64 m
$\displaystyle 35.2\degree$
46.12 m

49.

Answer.

$6.1\degree$

51.

Answer.

$triangle$

4.2

53.

Answer.

$triangle$

22.25 ft

55.

Answer.

79,332.6 AU

57.

Answer.

$OW$ bisects the central angle at $O\text{,}$ and the inscribed angle $\theta$ is half the central angle at $O\text{.}$
$\displaystyle \sin \theta = \dfrac{s}{2r}$
$\displaystyle r = \dfrac{s}{2 \sin (\theta)}$
$\displaystyle d = \dfrac{s}{\sin (\theta)}$

4 Trigonometric Functions
4.1 Angles and Rotation
Homework 4.1

1.

Answer.

$\displaystyle 216\degree$
$\displaystyle 108\degree$
$\displaystyle 480\degree$
$\displaystyle 960\degree$

3.

Answer.

$\displaystyle \dfrac{1}{8}$
$\displaystyle \dfrac{5}{6}$
$\displaystyle \dfrac{3}{2}$
$\displaystyle \dfrac{7}{6}$

5.

Answer.

$\displaystyle \dfrac{2}{3}$
$\displaystyle \dfrac{5}{3}$

7.

Answer.

$60\degree$

9.

Answer.

$60\degree$

11.

Answer.

$14\degree$

13.

Answer.

$400\degree$ and $-320\degree$ (Answers vary.)

15.

Answer.

$575\degree$ and $-145\degree$ (Answers vary.)

17.

Answer.

$665\degree$ and $-55\degree$ (Answers vary.)

19.

Answer.

$295\degree$

21.

Answer.

$70\degree$

23.

Answer.

$315\degree$

25.

Answer.

$\displaystyle 36.9\degree,~143.1\degree$
$angles on grid$

27.

Answer.

$\displaystyle 72.5\degree,~287.5\degree$
$graph$

29.

Answer.

$80\degree$

$angles$

31.

Answer.

$36\degree$

$angles$

33.

Answer.

$63\degree$

$angles$

35.

Answer.

$165\degree\text{,}$ $95\degree\text{,}$ $345\degree$

$angles$

37.

Answer.

$140\degree\text{,}$ $220\degree\text{,}$ $320\degree$

$angles$

39.

Answer.

$112\degree\text{,}$ $248\degree\text{,}$ $292\degree$

$angles$

41.

Answer.

$-0.9205$

43.

Answer.

$-0.7193$

45.

Answer.

$4.705$

47.

Answer.

$-0.7193$

49.

Answer.

$\displaystyle 120\degree$
$\displaystyle 135\degree$
$\displaystyle 150\degree$
$\displaystyle 210\degree$
$\displaystyle 225\degree$
$\displaystyle 240\degree$
$\displaystyle 300\degree$
$\displaystyle 315\degree$
$\displaystyle 330\degree$

51.

Answer.

$angles$
$\sin (120\degree) = \dfrac{\sqrt{3}}{2},~\cos (120\degree) = \dfrac{-1}{2},~\tan (120\degree) = -\sqrt{3},$

$\sin (240\degree) = \dfrac{-\sqrt{3}}{2},~\cos (240\degree) = \dfrac{-1}{2},~\tan (240\degree) = \sqrt{3},$

$\sin (300\degree) = \dfrac{-\sqrt{3}}{2},~\cos (300\degree) = \dfrac{1}{2},~\tan (300\degree) = -\sqrt{3}$

53.

Answer.

$angles$
$\sin (135\degree) = \dfrac{1}{\sqrt{2}},~\cos (135\degree) = \dfrac{-1}{\sqrt{2}},~(\tan 135\degree) = -1,$

$\sin (225\degree) = \dfrac{-1}{\sqrt{2}},~\cos (225\degree) = \dfrac{-1}{\sqrt{2}},~\tan (225\degree) = 1,$

$\sin (315\degree) = \dfrac{-1}{\sqrt{2}},~\cos (315\degree) = \dfrac{1}{\sqrt{2}},~\tan (315\degree) = -1$

55.

Answer.

III and IV
II and III
I and III

57.

Answer.

$\displaystyle 0\degree~ \text{and}~ 180\degree$
$\displaystyle 90\degree~ \text{and}~ 270\degree$

59.

Answer.

$105\degree$

61.

Answer.

$264\degree$

63.

Answer.

$313\degree$

65.

Answer.

Sides of similar triangles are proportional.

4.2 Graphs of Trigonometric Functions
Homework 4.2

1.

Answer.

$sine graph$

3.

Answer.

$cosine graph$

5.

Answer.

$\displaystyle \left(-225\degree, \dfrac{1}{\sqrt{2}}\right)$
$\displaystyle \left(-135\degree, \dfrac{-1}{\sqrt{2}}\right)$
$\displaystyle (-90\degree, -1)$
$\displaystyle \left(45\degree, \dfrac{1}{\sqrt{2}}\right)$
$\displaystyle (180\degree, 0)$
$\displaystyle \left(315\degree, \dfrac{-1}{\sqrt{2}}\right)$

7.

Answer.

$\displaystyle \left(-240\degree, \dfrac{-1}{2}\right)$
$\displaystyle \left(-210\degree, \dfrac{-\sqrt{3}}{2}\right)$
$\displaystyle \left(-60\degree, \dfrac{-1}{2}\right)$
$\displaystyle \left(30\degree, \dfrac{\sqrt{3}}{2}\right)$
$\displaystyle \left(120\degree, \dfrac{-1}{2}\right)$
$\displaystyle \left(270\degree, 0\right)$

9.

Answer.

$\theta$ $0\degree$ $90\degree$ $180\degree$ $270\degree$ $360\degree$

$f(\theta)$ $0$ $1$ $0$ $-1$ $0$

$cosine graph$
$\theta$ $0\degree$ $90\degree$ $180\degree$ $270\degree$ $360\degree$

$f(\theta)$ $1$ $0$ $-1$ $0$ $1$

$cosine graph$

11.

Answer.

$\dfrac{7}{2}$

13.

Answer.

$-2\sqrt{2} - 1$

15.

Answer.

$2$

17.

Answer.

$\dfrac{21}{2}$

19.

Answer.

$sine graph$

21.

Answer.

$graph$

23.

Answer.

$\theta$	$81\degree$	$82\degree$	$83\degree$	$84\degree$	$85\degree$	$86\degree$	$87\degree$	$88\degree$	$89\degree$
$\tan (\theta)$	$6.314$	$7.115$	$8.144$	$9.514$	$11.43$	$14.301$	$19.081$	$28.636$	$57.29$

$\displaystyle \tan (\theta)~ \text{approaches}~ \infty$

$\theta$	$99\degree$	$98\degree$	$97\degree$	$96\degree$	$95\degree$	$94\degree$	$93\degree$	$92\degree$	$91\degree$
$\tan (\theta)$	$-6.314$	$-7.115$	$-8.144$	$-9.514$	$-11.43$	$-14.301$	$-19.081$	$-28.636$	$-57.29$

$\displaystyle \tan (\theta)~ \text{approaches}~ -\infty$
The calculator gives an error message because $\tan (90\degree)$ is undefined.

25.

Answer.

$y = 6 \sin (\theta)$

27.

Answer.

$y = \cos (\theta) - 5$

29.

Answer.

$y = \sin (4\theta)$

31.

Answer.

$graph of y = 3 cos theta$

33.

Answer.

$graph of 3 + sin theta$

35.

Answer.

$graph of cos 3 theta$

37.

Answer.

$A(0\degree, -3)\text{,}$ $~B\left(135\degree, \dfrac{3}{\sqrt{2}}\right)\text{,}$ $~C\left(300\degree, \dfrac{-3}{2}\right)$

39.

Answer.

$P(112.5\degree, 1)\text{,}$ $~Q(180\degree, 0)\text{,}$ $~R(337.5\degree,-1)$

41.

Answer.

$X\left(45\degree, -3 + \dfrac{1}{\sqrt{2}}\right)\text{,}$ $~Y(90\degree, -3)\text{,}$ $~Z(300\degree,-2)$

43.

Answer.

amp$= 4\text{,}$ period $= 360\degree\text{,}$ midline: $y = 3$

45.

Answer.

amp$= 5\text{,}$ period $= 180\degree\text{,}$ midline: $y = 0$

47.

Answer.

amp$= 3\text{,}$ period $= 120\degree\text{,}$ midline: $y = -4$

49.

Answer.

amp $=1\text{,}$ period $=90\degree\text{,}$ midline: $y = 0$
$\displaystyle y = \sin (4\theta)$

51.

Answer.

amp $=1\text{,}$ period $=360\degree\text{,}$ midline: $y = 3$
$\displaystyle y = 3 + \cos (\theta)$

53.

Answer.

amp $=4\text{,}$ period $=360\degree\text{,}$ midline: $y = -2$
$\displaystyle y = -2 + 4\sin (\theta)$

55.

Answer.

amp $=2\text{,}$ period $=120\degree\text{,}$ midline: $y = 2$
$\displaystyle y = 2 + 2\cos (3\theta)$

57.

Answer.

$y = -4 + 6 \sin (3\theta)$ (Answers vary)

59.

Answer.

$y = 3 + 2 \cos (\theta)$ (Answers vary)

61.

Answer.

$y = 12 \cos (2\theta)$ (Answers vary)

63.

Answer.

$y = 2 + 5\cos (\theta)$

65.

Answer.

$y = -4\sin (\theta)$

4.3 Using Trigonometric Functions
Homework 4.3

1.

Answer.

$36.9\degree,~143.1\degree$

3.

Answer.

$72.5\degree,~287.5\degree$

5.

Answer.

$191.5\degree,~348.5\degree$

7.

Answer.

$154.2\degree,~205.8\degree$

9.

Answer.

$83\degree,~263\degree$

11.

Answer.

$23\degree,~337\degree$

13.

Answer.

$265\degree,~275\degree$

15.

Answer.

$156\degree,~204\degree$

17.

Answer.

$246\degree,~294\degree$

19.

Answer.

$149\degree,~329\degree$

21.

Answer.

$\displaystyle (-0.94, -0.34)$
$\displaystyle (-1.88, -0.68)$

23.

Answer.

$\displaystyle (-0.94, 0.34)$
$\displaystyle (-1.88, 0.68)$

25.

Answer.

$(4\sqrt{2},-4\sqrt{2})$

27.

Answer.

$(-10,-10\sqrt{3})$

29.

Answer.

$(\dfrac{-15\sqrt{3}}{2},\dfrac{15}{2})$

31.

Answer.

$(-1.25,-5.87)$

33.

Answer.

$(5.70, -11.86)$

35.

Answer.

$(9.46,-3.26)$

37.

Answer.

$angle$
15.3 mi east, 21 mi north

39.

Answer.

$angle$
91.9 km west, 77.1 km south

41.

Answer.

$angle$
30.9 km west, 8.3 km north

43.

Answer.

$51.34\degree$

45.

Answer.

$159.44\degree$

47.

Answer.

$y + 5 = (\tan 28\degree)(x - 3)~$ or $~y + 5 = 0.532(x - 3)$

49.

Answer.

$y - 12 = (\tan 112\degree)(x + 8)~$ or $~y - 12 = -2.475(x + 8)$

51.

Answer.

not periodic

53.

Answer.

Periodic with period 4

55.

Answer.

$piecewise linear graph$
10 minutes

57.

Answer.

$piercewise linear graph$
1 week

59.

Answer.

$sinusoidal graph$
period 1 sec, midline $y = 12\text{,}$ amp 10 inches

61.

Answer.

$sinusoidal graph$
period 1 year, midline $y = 3500\text{,}$ amp 2500

63.

Answer.

$sinusoidal graph$
period 1 year, midline $y = 51\text{,}$ amp 21

65.

Answer.

a. IV b. III c. II d. I

67.

Answer.

$two graphs$

69.

Answer.

Emotional high: Oct 5 and Nov 3, low: Oct 19; Physical high: Sep 30 and Oct 23, low: Oct 12 and Nov 4; Intellectual high: Oct 10, low: Oct 26
Emotional: 28 days, physical: 23 days, intellectual: 32 days
5152 days

71.

Answer.

periodic, period 8
4, midline: $y = 3$
$\displaystyle k = 8$
$\displaystyle a = 3,~b = 7$

73.

Answer.

systolic 120 mm Hg, diastolic 80 mm Hg, pulse pressure 40 mm Hg.
$\displaystyle 93\frac{1}{3}$
72 beats per minute

75.

Answer.

69 hours.
2.2 to 3.5
The larger dip corresponds to when the brighter star is eclipsed, the smaller dip corresponds to when the dimmer star is eclipsed.

4.4 Chapter 4 Summary and Review
Chapter 4 Review Problems

1.

Answer.

$12\degree$

3.

Answer.

$\displaystyle 150\degree,~ -210\degree$
$\displaystyle 240\degree,~ -120\degree$
$\displaystyle 160\degree,~ -560\degree$
$\displaystyle 20\degree,~ -340\degree$

5.

Answer.

$\displaystyle I,~60\degree;~ 120\degree,~ 240\degree,~ 300\degree$
$\displaystyle IV,~25\degree;~ 155\degree,~ 205\degree,~ 335\degree$
$\displaystyle II,~80\degree;~ 80\degree,~ 260\degree,~ 280\degree$
$\displaystyle III,~70\degree;~ 70\degree,~ 110\degree,~ 290\degree$

7.

Answer.

\(\theta\)
\(30\degree\)
\(60\degree\)
\(90\degree\)
\(120\degree\)
\(150\degree\)
\(180\degree\)
\(210\degree\)
\(240\degree\)
\(270\degree\)
\(300\degree\)
\(330\degree\)
\(360\degree\)

\(f(\theta)\)
\(30\)
\(60\)
\(90\)
\(60\)
\(30\)
\(0\)
\(30\)
\(60\)
\(90\)
\(60\)
\(30\)
\(0\)

$graph of referance angle vs angle$

9.

Answer.

$210\degree,~ 330\degree$

11.

Answer.

$120\degree,~ 240\degree$

13.

Answer.

$45\degree,~ 225\degree$

15.

Answer.

$23\degree,~ 337\degree$

17.

Answer.

$72\degree,~ 252\degree$

19.

Answer.

$163\degree,~ 277\degree$

21.

Answer.

$221.81\degree,~ 318.19\degree$

23.

Answer.

$123.69\degree,~ 303.69\degree$

25.

Answer.

$128.68\degree,~ 231.32\degree$

27.

Answer.

$(-9.74, -2.25)$

29.

Answer.

$(-0.28, 8.00)$

31.

Answer.

$(2.84, 0.98)$

33.

Answer.

south: 1.74 mi, west: 9.85 mi

35.

Answer.

$y = 4 + 7 \sin (180\theta)$

$sinusoidal graph$

37.

Answer.

$y = 17 + 7 \sin \theta$

$sinusoidal graph$

39.

Answer.

$\dfrac{\sqrt{3}}{2}$

41.

Answer.

43.

Answer.

$y = 1.5 \cos (\dfrac{\theta}{3}),~ M(-90\degree, \dfrac{3\sqrt{3}}{4}), N(180\degree, \dfrac{3}{4})$

45.

Answer.

$y = 3 + 3 \sin 2\theta,~ A(-45\degree, 6), B(120\degree, 3 - \dfrac{3\sqrt{3}}{2})$

47.

Answer.

$periodic graph$
24 hours

49.

Answer.

$periodic graph$
20 sec

51.

Answer.

$y = 4 + 2 cos theta$
amp: 2, period: $360\degree\text{,}$ midline: $y = 4$

53.

Answer.

$y = 1.5 + 3.5 sin (2 theta)$
amp: 3.5, period: $180\degree\text{,}$ midline: $y = 1.5$

55.

Answer.

$30\degree$

57.

Answer.

$92.05\degree$

59.

Answer.

$y = x + 2$

61.

Answer.

$y = -\sqrt{3} x + 3\sqrt{3} - 4$

63.

Answer.

$cosine and tangent graphs$

The $\theta$-intercepts of $\cos \theta$ occur at the vertical asymptotes of $\tan \theta\text{.}$

5 Equations and Identities
5.1 Algebra with Trigonometric Ratios
Homework 5.1

1.

Answer.

$-2$

3.

Answer.

$\dfrac{1}{\sqrt{2}}$

5.

Answer.

$6$

7.

Answer.

$\dfrac{1}{2}$

9.

Answer.

$4$

11.

Answer.

$2$

13.

Answer.

$1$

15.

Answer.

$0$

17.

Answer.

$\displaystyle 0.7660$
$\displaystyle 0.8164$
$\displaystyle 0.7660$

19.

Answer.

$\displaystyle 0.6691$
$\displaystyle 1.8271$
$\displaystyle 0.6691$

21.

Answer.

$\displaystyle 1$
$\displaystyle 1$
$\displaystyle 1$

23.

Answer.

$\displaystyle -2x^2 - x$
$\displaystyle -2\cos^2 (\theta) - \cos (\theta)$

25.

Answer.

$\displaystyle 4SC$
$\displaystyle 4\sin (\theta) \cos (\theta)$

27.

Answer.

$\displaystyle 5C^2S^3$
$\displaystyle 5\cos^2 (\theta) \sin^3 (\theta) $

29.

Answer.

$-2\cos (t) + 2 \cos (t) \sin (t); ~ 0.6360$

31.

Answer.

$\tan (\theta) - \tan (\phi); ~ -56.91$

33.

Answer.

$2\sin (x) \cos (x) - 2\sin (2x); ~ 0$

35.

Answer.

37.

Answer.

39.

Answer.

Yes

41.

Answer.

43.

Answer.

45.

Answer.

$\displaystyle 2x^2 - x$
$\displaystyle 2\sin^2 (A) - \sin (A)$

47.

Answer.

$\displaystyle ab - 3a^2$
$\displaystyle \tan (A) \tan (B) - 3 \tan^2 (A)$

49.

Answer.

$\displaystyle 2C^2 + C - 1$
$\displaystyle 2\cos^2 (\phi) + \cos (\phi) - 1$

51.

Answer.

$\displaystyle a^2 - b^2$
$\displaystyle \cos^2 (\theta) -\cos^2 (\phi)$

53.

Answer.

$\displaystyle 1 - 2T + T^2$
$\displaystyle 1 - 2\tan (\theta) + \tan^2 (\theta)$

55.

Answer.

$\displaystyle T^4 - 4$
$\displaystyle \tan^4 (\theta) - 4$

57.

Answer.

$\displaystyle 3(3m + 5n)$
$\displaystyle 3\Big(3\cos(\alpha) + 5\cos(\beta)\Big)$

59.

Answer.

$\displaystyle 5r(r - 2q)$
$\displaystyle 5\tan (C) \Big(\tan (C) - 2 \tan (B)\Big)$

61.

Answer.

$\displaystyle (3C+1)(3C-1)$
$\displaystyle \Big(3\cos (\beta) + 1\Big)\Big(3\cos (\beta) - 1\Big)$

63.

Answer.

$\displaystyle 2T^2(3T - 4)$
$\displaystyle 2\tan^2 (A)\Big(3\tan (A) - 4\Big)$

65.

Answer.

$\displaystyle (t - 5)(t + 4)$
$\displaystyle \Big(\tan (\theta) - 5\Big)\Big(\tan (\theta) + 4\Big)$

67.

Answer.

$\displaystyle (3c - 1)(c + 1)$
$\displaystyle \Big(3\cos (B) - 1\Big)\Big(\cos (B) + 1\Big)$

69.

Answer.

$\displaystyle (6S + 1)(S - 1)$
$\displaystyle \Big(6\sin (\alpha) + 1\Big)\Big(\sin (\alpha) - 1\Big)$

5.2 Solving Equations
Homework 5.2

1.

Answer.

$70\degree$

3.

Answer.

$40\degree$

5.

Answer.

I: $18\degree;$ II: $162\degree;$ III: $198\degree;$ IV: $342\degree$

7.

Answer.

I: $52\degree;$ II: $128\degree;$ III: $232\degree;$ IV: $308\degree$

9.

Answer.

$\displaystyle 0,~4,~2,~0,~4$
$\displaystyle -1~\text{or}~2$

11.

Answer.

$\displaystyle 1,~\dfrac{\sqrt{3}+1}{2},~\sqrt{2},~\dfrac{\sqrt{3}+1}{2}$
$\displaystyle 45\degree$

13.

Answer.

$\displaystyle 0,~\dfrac{2-\sqrt{2}}{2},~\dfrac{1 -\sqrt{3}}{2},~-1$
$\displaystyle 270\degree$

15.

Answer.

$x = 5,~-3$

17.

Answer.

$x = -3,~1,~2$

19.

Answer.

$\theta = 30\degree ~$ or $~ \theta = 210\degree$

21.

Answer.

$\theta = 60\degree ~$ or $~ \theta = 300\degree$

23.

Answer.

$\theta = 210\degree ~$ or $~ \theta = 330\degree$

25.

Answer.

$\theta = 225\degree ~$ or $~ \theta = 315\degree$

27.

Answer.

$\theta = 0\degree ~$ or $~ \theta = 180\degree$

29.

Answer.

$\theta = 60\degree, ~\theta = 120\degree,~\theta = 240\degree,~$ or $~ \theta = 300\degree$

31.

Answer.

$\theta = 45\degree,~\theta = 135\degree,~\theta = 225\degree, ~$ or $~ \theta = 315\degree$

33.

Answer.

$\theta = 104.04\degree ~$ or $~ \theta = 284.04\degree$

35.

Answer.

$\theta = 53.13\degree ~$ or $~ \theta = 306.87\degree$

37.

Answer.

$\theta = 188.21\degree ~$ or $~ \theta = 351.79\degree$

39.

Answer.

$A = 135\degree ~$ or $~ A = 315\degree$

41.

Answer.

$\phi = 210\degree ~$ or $~ \phi = 330\degree$

43.

Answer.

$B = 90\degree ~\text{or}~ B = 270\degree$

45.

Answer.

$\theta = 210\degree ~$ or $~ \theta = 330\degree$

47.

Answer.

$t = 202\degree ~$ or $~t = 338\degree$

49.

Answer.

$B = 22\degree ~\text{or}~ B = 202\degree$

51.

Answer.

$\phi = 146\degree ~$ or $~ \phi = 214\degree$

53.

Answer.

$\theta = 54.74\degree, ~\theta = 125.26\degree,~\theta = 234.74\degree,~$ or $~ \theta = 305.26\degree$

55.

Answer.

$\theta = 0\degree\text{,}$ $~\theta = 180\degree\text{,}$ $~\theta = 191.54\degree,~$ or $~ \theta = 348.46\degree$

57.

Answer.

$\theta = 60\degree\text{,}$ $~ \theta = 180\degree\text{,}$ or $~ \theta = 300\degree$

59.

Answer.

$\theta = 26.57\degree\text{,}$ $~\theta = 161.57\degree\text{,}$ $~\theta = 206.57\degree\text{,}$ or $~ \theta = 341.57\degree$

61.

Answer.

$\theta = 78.69\degree\text{,}$ $~\theta = 108.43\degree\text{,}$ $~\theta = 258.69\degree\text{,}$ or $~ \theta = 288.43\degree$

63.

Answer.

$\theta = 0\degree$

65.

Answer.

$17.22\degree$

67.

Answer.

$35.66\degree$

5.3 Trigonometric Identities
Homework 5.3

1.

Answer.

not an identity

3.

Answer.

not an identity

5.

Answer.

identity

7.

Answer.

not an identity

9.

Answer.

not an identity

11.

Answer.

not an identity

13.

Answer.

identity

15.

Answer.

identity

17.

Answer.

$(1 + \sin (w))(1 - \sin (w)) = 1 - \sin^2 (w) = \cos^2 (w)$

19.

Answer.

\begin{equation*} \begin{aligned}[t] \Big(\cos (\theta) - \sin (\theta)\Big)^2 \amp = \cos^2 (\theta) - 2\cos (\theta) \sin (\theta) + \sin^2 (\theta)\\ \amp = \Big(\cos^2 (\theta )+ \sin^2 (\theta)\Big) - 2\sin(\theta) \cos (\theta) = 1 - 2\sin(\theta) \cos (\theta)\\ \end{aligned} \end{equation*}

21.

Answer.

$\tan (\theta) \cos (\theta) = \dfrac{\sin (\theta)}{\cos (\theta)}\cdot \cos (\theta) = \sin (\theta) $

23.

Answer.

\begin{equation*} \begin{aligned}[t] \cos^4 (x) - \sin^4 (x) \amp = \Big(\cos^2 (x) - \sin^2 (x)\Big)\Big(\cos^2 (x) + \sin^2 (x)\Big)\\ \amp = \Big(\cos^2 (x) - \sin^2 (x)\Big)(1) = \cos^2 (x) - \sin^2 (x)\\ \end{aligned} \end{equation*}

25.

Answer.

$\dfrac{\sin (u)}{1 + \cos (u)} \cdot \dfrac{1 - \cos (u)}{1 - \cos (u)} = \dfrac{\sin (u)\Big(1 - \cos (u)\Big)}{1 - \cos^2 (u)} = \dfrac{\sin (u)\Big(1 - \cos (u)\Big)}{\sin^2 (u)} = \dfrac{1 - \cos (u)}{\sin (u)}$

27.

Answer.

$1$

29.

Answer.

$1$

31.

Answer.

$\sin^2 (A)$

33.

Answer.

$\tan^2 (z)$

35.

Answer.

$3$

37.

Answer.

$1$

39.

Answer.

$6$

41.

Answer.

$\cos (2\theta)$

43.

Answer.

$\cos (\theta)$

45.

Answer.

$\sin (2t)$

47.

Answer.

$1 + 2\sin (\theta) + \sin^2 (\theta)$

49.

Answer.

$3\cos^2 (\phi) - 2$

51.

Answer.

$\theta = 90\degree, ~\theta = 180\degree, ~\theta = 270\degree$

53.

Answer.

$\theta = 90\degree, ~\theta = 210\degree, ~\theta = 330\degree$

55.

Answer.

$\theta = 210\degree, ~\theta = 330\degree$

57.

Answer.

$\theta = 18.43\degree,~ \theta = 198.43\degree$

59.

Answer.

$\sin (A) = \dfrac{-5}{13},~ \tan (A) = \dfrac{-5}{12}$

61.

Answer.

$\cos (\phi) = \dfrac{-4\sqrt{3}}{7},~ \tan (\phi) = \dfrac{-1}{4\sqrt{3}}$

63.

Answer.

$\sin (\theta) =\dfrac{-1}{\sqrt{5}}\text{,}$ $~ \cos (\theta) = \dfrac{2}{\sqrt{5}}$

65.

Answer.

$\sin (\theta) =\dfrac{-3}{5}\text{,}$ $~ \cos (\theta) = \dfrac{-4}{5}$

67.

Answer.

$\sin (\theta) =\dfrac{\sqrt{3}}{2}\text{,}$ $~ \cos (\theta) = \dfrac{-1}{2}\text{,}$ $~ \tan (\theta) = \sqrt{3}$

69.

Answer.

$\sin (\beta) =\dfrac{2}{\sqrt{5}}\text{,}$ $~ \cos (\beta) = \dfrac{-1}{\sqrt{5}}\text{,}$ $~ \tan (\beta) = -2$

71.

Answer.

\begin{equation*} \begin{aligned}[t] \amp \sin (C) =\dfrac{1}{\sqrt{5}},~ \cos (C) = \dfrac{2}{\sqrt{5}},~ \tan (C) = \dfrac{1}{2}\\ \text{or}~~\amp \sin (C) =\dfrac{1}{\sqrt{5}},~ \cos (C) = \dfrac{-2}{\sqrt{5}},~ \tan (C) = \dfrac{-1}{2}\\ \end{aligned} \end{equation*}

73.

Answer.

$\dfrac{\tan (\alpha)}{1 + \tan (\alpha)} = \dfrac{\dfrac{\sin (\alpha)}{\cos (\alpha)}}{1 + \dfrac{\sin (\alpha)}{\cos (\alpha)}} \cdot \dfrac{\cos (\alpha)}{\cos (\alpha)} = \dfrac{\sin (\alpha)}{\sin (\alpha) + \cos (\alpha)}$

75.

Answer.

$\dfrac{1 + \tan^2 (\beta)}{1 - \tan^2 (\beta)} = \dfrac{\dfrac{1}{\cos^2 (\beta)}}{1 - \dfrac{\sin^2 (\beta)}{\cos^2 (\beta)}} \cdot \dfrac{\cos^2 (\beta)}{\cos^2 (\beta)} = \dfrac{1}{\cos^2 (\beta) - \sin^2 (\beta)}$

77.

Answer.

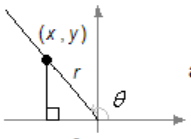
By the distance formula, $\sqrt{x^2 + y^2} = r\text{,}$ or $x^2 + y^2 = r^2\text{.}$
$\displaystyle \dfrac{x^2}{r^2} + \dfrac{y^2}{r^2} = 1$
$\displaystyle \left(\dfrac{x}{r}\right)^2 + \left(\dfrac{y}{r}\right)^2 = 1$
$\displaystyle \Big(\cos (\theta)\Big)^2 + \Big(\sin (\theta)\Big)^2 = 1$

5.4 Chapter 5 Summary and Review
Chapter 5 Review Problems

1.

Answer.

$\dfrac{-3}{4\sqrt{2}}$

3.

Answer.

$\dfrac{1}{\sqrt{6}}$

5.

Answer.

$\displaystyle 0.8660$
$0.9848;$ No

7.

Answer.

$\displaystyle 1.4821$
$1.4821;$ Yes

9.

Answer.

$5\sin (x) - 2\sin (x) \cos (y) - \cos (y)$

11.

Answer.

$2\tan (\theta) - 10\tan^2 (\theta)$

13.

Answer.

Not equivalent

15.

Answer.

Equivalent

17.

Answer.

$2\cos^2 \alpha + \cos \alpha - 6$

19.

Answer.

$\tan^2 (\phi) - 2\tan (\phi) \cos (\phi) + \cos^2 (\phi)$

21.

Answer.

$6\Big(2\sin (3x) - \sin (2x)\Big)$

23.

Answer.

$\Big(1 + 3\tan (\theta)\Big)\Big(1 - 3\tan (\theta)\Big)$

25.

Answer.

$\cos (\alpha) + \sin (\alpha)$

27.

Answer.

$\dfrac{3}{2}$

29.

Answer.

$\dfrac{3\tan (C) + 2}{\tan (C) - 2}$

31.

Answer.

$51.32\degree,~ 308.68\degree$

33.

Answer.

$90\degree\text{,}$ $~ 270\degree\text{,}$ $~ 120\degree\text{,}$ $~ 240\degree$

35.

Answer.

$90\degree\text{,}$ $~ 210\degree\text{,}$ $~ 330\degree$

37.

Answer.

$30\degree\text{,}$ $~ 150\degree\text{,}$ $~ 210\degree\text{,}$ $~ 330\degree$

39.

Answer.

$0\degree\text{,}$ $~ 120\degree\text{,}$ $~ 240\degree$

41.

Answer.

$57.99\degree,~ 237.99\degree$

43.

Answer.

$90\degree,~ 270\degree$

45.

Answer.

$33.17\degree$

47.

Answer.

Identity

49.

Answer.

Not an identity

51.

Answer.

Not an identity

53.

Answer.

Identity

55.

Answer.

$\dfrac{1 - \cos^2 (\alpha)}{\tan (\alpha)} = \sin^2 (\alpha) \cdot \dfrac{\cos (\alpha)}{\sin (\alpha)} = \sin (\alpha) \cos (\alpha)$

57.

Answer.

\begin{equation*} \begin{aligned}[t] \dfrac{\dfrac{\sin (\theta)}{\cos (\theta)} - \sin (\theta) \cos (\theta)}{\sin (\theta) \cdot \dfrac{\sin (\theta)}{\cos (\theta)}} \amp = \dfrac{\sin (\theta) - \sin (\theta) \cos^2 (\theta)}{\sin^2 (\theta)}\\ \amp = \dfrac{\sin (\theta) \Big(1 - \cos^2 (\theta)\Big)}{\sin^2 (\theta)} = \dfrac{\sin (\theta) \sin^2 (\theta)}{\sin^2 (\theta)} = \sin (\theta)\\ \end{aligned} \end{equation*}

59.

Answer.

$\dfrac{1}{\sin (\theta) \cos (\theta)}$

61.

Answer.

$1$

63.

Answer.

$0$

65.

Answer.

$1$

67.

Answer.

$\dfrac{1}{\cos^2 (\beta)}$

69.

Answer.

$\sin (x)$

71.

Answer.

$\sin (\beta) = \dfrac{-6}{\sqrt{85}},~ \cos (\beta) = \dfrac{-7}{\sqrt{85}},~ \tan (\beta) = \dfrac{6}{7}$

73.

Answer.

$\sin (\alpha) = \dfrac{\sqrt{21}}{5},~ \cos (\alpha) = \dfrac{-2}{5},~ \tan (\alpha) = \dfrac{-\sqrt{21}}{2}$

75.

Answer.

$0\degree,~ 180\degree,~ 270\degree$

77.

Answer.

$135\degree,~ 315\degree$

79.

Answer.

$0\degree,~ 60\degree,~ 180\degree,~ 300\degree$

81.

Answer.

$0\degree,~ 180\degree$

6 Radians
6.1 Arclength and Radians
Homework 6.1

1.

Answer.

Radians	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2 \pi$
Degrees	$0\degree$	$45\degree$	$90\degree$	$135\degree$	$180\degree$	$225\degree$	$270\degree$	$315\degree$	$360\degree$

$circle$

3.

Answer.

$\displaystyle 120\degree = \dfrac{2\pi}{3} \text{radians}$
$\displaystyle 240\degree = \dfrac{4\pi}{3} \text{radians}$
$\displaystyle 480\degree = \dfrac{8\pi}{3} \text{radians}$
$\displaystyle 600\degree = \dfrac{10\pi}{3} \text{radians}$

5.

Answer.

$\displaystyle 45\degree = \dfrac{\pi}{4} \text{radians}$
$\displaystyle 135\degree = \dfrac{3\pi}{4} \text{radians}$
$\displaystyle 225\degree = \dfrac{5\pi}{4} \text{radians}$
$\displaystyle 315\degree = \dfrac{7\pi}{4} \text{radians}$

7.

Answer.

$circle$

9.

Answer.

$\displaystyle 0.52$
$\displaystyle 2.62$
$\displaystyle 3.67$
$\displaystyle 5.76$

11.

Answer.

$circle$

13.

Answer.

$2.09$

15.

Answer.

$2.62$

17.

Answer.

$0.52$

19.

Answer.

$2.36$

21.

Answer.

23.

Answer.

25.

Answer.

Radians	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$
Degrees	$30\degree$	$45\degree$	$60\degree$

27.

Answer.

Radians	$\dfrac{7\pi}{6}$	$\dfrac{5\pi}{4}$	$\dfrac{4\pi}{3}$
Degrees	$210\degree$	$225\degree$	$240\degree$

29.

Answer.

$\displaystyle 1.31$
$\displaystyle 4.12$
$\displaystyle 5.71$

31.

Answer.

$\displaystyle 45.8\degree$
$\displaystyle 200.5\degree$
$\displaystyle 292.2\degree$

33.

Answer.

$5.86~\text{in}$

35.

Answer.

$4.13~\text{m}$

37.

Answer.

$160.42\degree$

39.

Answer.

$\displaystyle \dfrac{5\pi}{6}$
$\displaystyle 32.72~\text{ft}$

41.

Answer.

$\dfrac{8}{67}~\text{radians}~\approx6.84\degree$

43.

Answer.

$\displaystyle 33,000\pi\approx 103,672.6~\text{in}$
$\displaystyle 33,000\pi\approx 103.672.6~\text{in per min}$

45.

Answer.

$170\pi\approx 534.1~\text{m per min}$

47.

Answer.

$unit circle$

$(0.2,0.98)\text{,}$ $~(0.2,-0.98)$

49.

Answer.

$unit circle$

$(0.94,-0.35)\text{,}$ $~(-0.94,-0.35)$

51.

Answer.

$unit circle$

$\left(\dfrac{-\sqrt{3}}{2}, \dfrac{1}{2}\right)\text{,}$ $~\left(\dfrac{-\sqrt{3}}{2}, \dfrac{-1}{2}\right)$

53.

Answer.

$circle$
$\theta$ $1$ $2$ $3$ $4$ $5$ $6$

$s$ $4$ $8$ $12$ $16$ $20$ $24$
$linear graph of arclength vs angle$

$\displaystyle m = 4$
Arclength doubles; arclength triples

55.

Answer.

$\displaystyle \dfrac{\pi}{10}~\text{radians per min}$
$\displaystyle \dfrac{10\pi}{9}~\text{radians per sec}$

57.

Answer.

$\displaystyle \dfrac{\theta}{2\pi}$
$\displaystyle \dfrac{3}{8},~\dfrac{5}{6},~\dfrac{7}{12}$

59.

Answer.

$32.5~\text{cm}^2$

6.2 The Circular Functions
Homework 6.2

1.

Answer.

$\hphantom{0000}$	a	b	c	d
$t$	$\dfrac{\pi}{4}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{4}$	$\dfrac{7\pi}{4}$
$x$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{-1}{\sqrt{2}}$	$\dfrac{-1}{\sqrt{2}}$	$\dfrac{1}{\sqrt{2}}$
$y$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{-1}{\sqrt{2}}$	$\dfrac{-1}{\sqrt{2}}$

3.

Answer.

$\hphantom{0000}$	a	b	c	d
$t$	$\dfrac{\pi}{3}$	$\dfrac{2\pi}{3}$	$\dfrac{4\pi}{3}$	$\dfrac{5\pi}{3}$
$x$	$\dfrac{1}{2}$	$\dfrac{-1}{2}$	$\dfrac{-1}{2}$	$\dfrac{1}{2}$
$y$	$\dfrac{\sqrt{3}}{2}$	$\dfrac{\sqrt{3}}{2}$	$\dfrac{-\sqrt{3}}{2}$	$\dfrac{-\sqrt{3}}{2}$

5.

Answer.

$\displaystyle \sin (0.4) \approx 0.39,~ \cos (0.4) \approx 0.92,~ \tan (0.4) \approx 0.42$
$\displaystyle \sin (1.2) \approx 0.93,~ \cos (1.2) \approx 0.36,~ \tan (1.2) \approx 2.6$
$\displaystyle \sin (2) \approx 0.91,~ \cos (2) \approx -0.42,~ \tan (2) \approx -2.2$

7.

Answer.

$\displaystyle \sin (2.8) \approx 0.33,~ \cos (2.8) \approx -0.94,~ \tan (2.8) \approx -0.36$
$\displaystyle \sin (3.5) \approx -0.35,~ \cos (3.5) \approx -0.94,~ \tan (3.5) \approx 0.37$
$\displaystyle \sin (5) \approx -0.96,~ \cos (5) \approx 0.28,~ \tan (5) \approx -3.3$

9.

Answer.

$t \approx 1.27$ or $t \approx 5$

11.

Answer.

$t \approx 3.92$ or $t \approx 5.5$

13.

Answer.

$t \approx 2.72$ or $t \approx 5.87$

15.

Answer.

17.

Answer.

19.

Answer.

III

21.

Answer.

Negative

23.

Answer.

Positive

25.

Answer.

Positive

27.

Answer.

$\sin (3.5)\text{,}$ $\sin (0.5)\text{,}$ $\sin (2.5)\text{,}$ $\sin (1.5)$

29.

Answer.

$\cos (3)\text{,}$$\cos (4)\text{,}$ $\cos (2)\text{,}$ $\cos (5)$

31.

Answer.

January 1: 4:24, April 1: 6:45, July 1: 8:02, October 1: 5:55

33.

Answer.

$1.34$

35.

Answer.

$0.84$

37.

Answer.

$0.02$

39.

Answer.

$\dfrac{1}{12}\pi$

41.

Answer.

$\dfrac{1}{3}\pi$

43.

Answer.

$\dfrac{1}{4}\pi$

45.

Answer.

$\dfrac{5\pi}{6}\text{,}$ $~\dfrac{7\pi}{6}\text{,}$ $~\dfrac{11\pi}{6}$

$circle$
$\dfrac{3\pi}{4}\text{,}$ $~\dfrac{5\pi}{4}\text{,}$ $~\dfrac{7\pi}{4}$

$circle$
$\dfrac{2\pi}{3}\text{,}$ $~\dfrac{4\pi}{3}\text{,}$ $~\dfrac{5\pi}{3}$

$circle$

47.

Answer.

$~\theta~$	$~~~\sin (\theta)~~~$	$~~~\cos (\theta)~~~$	$~~~\tan (\theta)~~~$
$\dfrac{7\pi}{6}$	$\dfrac{-1}{2}$	$\dfrac{-\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{3}}$
$\dfrac{5\pi}{4}$	$\dfrac{-1}{\sqrt{2}}$	$\dfrac{-1}{\sqrt{2}}$	$1$
$\dfrac{4\pi}{3}$	$\dfrac{-\sqrt{3}}{2}$	$\dfrac{-1}{2}$	$\sqrt{3}$

49.

Answer.

$\dfrac{1}{4}$

51.

Answer.

$-\dfrac{3+\sqrt{3}}{3}$

53.

Answer.

$\dfrac{3-6\sqrt{3}}{4}$

55.

Answer.

$(\cos (2.5),\sin (2.5)) \approx (-0.8, 0.6)$

57.

Answer.

$(\cos (8.5), \sin (8.5)) \approx (-0.6, 0.8)$

59.

Answer.

$\cos (5) \approx 0.28$ mi east, $\sin (5) \approx -0.96$ mi north, or about 0.96 mi south

61.

Answer.

$1.75$

63.

Answer.

$5.8$

65.

Answer.

$3.84$

67.

Answer.

$circle$

Intersections: $\left(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right)$ and $\left(\dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}}\right)$
$(\cos\left(\dfrac{\pi}{4}\right),\sin\left(\dfrac{\pi}{4}\right))$ and $\left(\cos\left(\dfrac{5\pi}{4}\right),\sin\left(\dfrac{5\pi}{4}\right)\right)$

69.

Answer.

$graph$

$\displaystyle m = \dfrac{3}{8}$
$\displaystyle \tan^{-1}(\frac{3}{8})\approx 0.3588$

71.

Answer.

$y - 2 = \sqrt{3}(x - 4)$

73.

Answer.

$y + 8 = (\tan (2.4))((x - 5)$ or $y + 8 = -0.916(x - 5)$

75.

Answer.

Any point $(x,y)$ on the terminal side of $\theta$ satisfies $\cos (\theta) = \dfrac{x}{r}\text{,}$ $~ \sin (\theta) = \dfrac{y}{r}\text{.}$ For the point $P$ where $r = 1\text{,}$ $~\cos (\theta) = x\text{,}$ $~\sin (\theta) = y\text{.}$ The arc of length $t$ is spanned by an angle $\theta$ in standard position. Because arclength is $r\theta$ and $r = 1\text{,}$ $~ t = \theta,$ so $x = \cos (t)\text{,}$ $~ y = \sin (t)\text{.}$

77.

Answer.

The two right triangles shown are similar, so their sides are proportional. The hypotenuse of the large triangle is $r$ times the hypotenuse of the small triangle, so the two legs of the large triangle must be $r$ times the legs of the small triangle. Thus, because the coordinates of the vertex on the unit circle are $(\cos (\theta), \sin (\theta))\text{,}$ the coordinates of $P$ must be $(r\cos (\theta), r\sin (\theta))\text{.}$

79.

Answer.

71 m west, 587 m north

6.3 Graphs of the Circular Functions
Homework 6.3

1.

Answer.

\(\theta\)
\(0\)
\(\dfrac{\pi}{12}\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{5\pi}{12}\)
\(\dfrac{\pi}{2}\)
\(\dfrac{7\pi}{12}\)
\(\dfrac{2\pi}{3}\)
\(\dfrac{3\pi}{4}\)
\(\dfrac{5\pi}{6}\)
\(\dfrac{11\pi}{12}\)
\(\pi\)

\(\cos (\theta)\)
\(1\)
\(0.97\)
\(0.87\)
\(0.71\)
\(0.50\)
\(0.26\)
\(0\)
\(-0.26\)
\(-0.50\)
\(-0.71\)
\(-0.87\)
\(-0.97\)
\(-1\)

$cosine graph$

3.

Answer.

$sine graph$

5.

Answer.

$sine graph$
Domain: $(-\infty, \infty)\text{,}$ range: $[-1,1]$

7.

Answer.

$tangent graph$
Domain: $x \ne \dfrac{n\pi}{2},~n$ an odd integer, range: $(-\infty, \infty)$

9.

Answer.

$x \approx 0.7$ or $x \approx 2.4$
$x \approx 0.36$ or $x \approx 2.78$

11.

Answer.

$x \approx 2$ or $x \approx 4.3$
$x \approx 2.5$ or $x \approx 3.79$

13.

Answer.

$x \approx 1.3$ or $x \approx 4.5$

15.

Answer.

$x \approx 2.7$ or $x \approx 5.8$

17.

Answer.

$x \approx 1.4$ or $x \approx 4.5$

19.

Answer.

$x \approx 2.2$ or $x \approx 5.3$

21.

Answer.

I: 0.5, II: 2.7, III: 3.6, IV: 5.8

23.

Answer.

I: 0.6, II: 2.6, III: 3.7, IV: 5.7

25.

Answer.

I: 1.3, II: 1.8, III: 4.5, IV: 4.9

27.

Answer.

$t \approx 0.74$ or $t \approx 5.55$

29.

Answer.

$t \approx 1.01$ or $t \approx 4.15$

31.

Answer.

$x \approx 3.94$ or $x \approx 5.48$

33.

Answer.

$t = \dfrac{3\pi}{2}$

35.

Answer.

$x = \dfrac{\pi}{4}~$ or $~x = \dfrac{5\pi}{4}$

37.

Answer.

$z = \dfrac{\pi}{3}~$ or $~z = \dfrac{5\pi}{3}$

39.

Answer.

$s = \dfrac{2\pi}{3}~$ or $~s = \dfrac{5\pi}{3}$

41.

Answer.

$t = \dfrac{5\pi}{4}~$ or $~t = \dfrac{7\pi}{4}$

43.

Answer.

$x = \dfrac{5\pi}{6}~$ or $~x = \dfrac{7\pi}{6}$

45.

Answer.

$\displaystyle 0.78$
$\displaystyle 1.12$

47.

Answer.

$\displaystyle 0.26$
$\displaystyle 1.28$

49.

Answer.

$\displaystyle -0.9$
No solution

51.

Answer.

$\displaystyle \dfrac{1}{\sqrt{2}}$
$\displaystyle 0.9$

53.

Answer.

$-6\sqrt{2}$

55.

Answer.

$-4\sqrt{3}$

57.

Answer.

$6$

59.

Answer.

b-c.

$sinusoidal graph$

d. $t \approx 10$ and $t \approx 20~~~$ e. $t \approx 7.5$ to $t \approx 22$

61.

Answer.

b-c.

$sinusoidal graph$

d. High: day 204, $105\degree\text{;}$ low: day 25, $66\degree$ e. $d \approx 128$ to $d \approx 281$

63.

Answer.

$\displaystyle -0.8,~ 0.6,~ \dfrac{-4}{3}$
$\displaystyle 0.8,~ -0.6,~ \dfrac{-4}{3}$
$\displaystyle -0.8,~ -0.6,~ \dfrac{4}{3}$

65.

Answer.

$\displaystyle 0.92,~ -0.39,~ \dfrac{-92}{39}$
$\displaystyle -0.92,~ 0.39,~ \dfrac{-92}{39}$
$\displaystyle 0.92,~ 0.39,~ \dfrac{92}{39}$

67.

Answer.

$three trig graphs$

69.

Answer.

$three trig graphs$

71.

Answer.

$parabola$
Domain: $(-\infty, \infty)\text{,}$ range: $(-\infty, 9]$

73.

Answer.

$graph of 2 - 1/(x^2)$
Domain: $x \ne 0\text{,}$ range: $(-\infty, 2)$

75.

Answer.

$graph of translated square root$
Domain: $[6, \infty)\text{,}$ range: $[0, \infty)$

77.

Answer.

$semicircle$
Domain: $[-2,2]\text{,}$ range: $[-2,0]$

79.

Answer.

$x$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$\cos (x)$ $1$ $0$ $-1$ $0$ $1$

$cosine graph$
Domain: $(-\infty, \infty) \text{,}$ Range: $[-1,1]$

6.4 Chapter 6 Summary and Review
Chapter 6 Review Problems

1.

Answer.

$\displaystyle \dfrac{5\pi}{12}$
$\displaystyle \dfrac{7\pi}{6}$
$\displaystyle \dfrac{17\pi}{9}$

3.

Answer.

$\displaystyle 0.47$
$\displaystyle 2.48$
$\displaystyle 3.80$

5.

Answer.

$\displaystyle 150\degree$
$\displaystyle 54\degree$
$\displaystyle 230\degree$

7.

Answer.

$\displaystyle 114.59\degree$
$\displaystyle 206.26\degree$
$\displaystyle 45.84\degree$

9.

Answer.

$\displaystyle \dfrac{4\pi}{3}$
$\displaystyle \dfrac{7\pi}{6}$
$\displaystyle \dfrac{9\pi}{4}$

11.

Answer.

$\displaystyle \dfrac{1}{8}$
$\displaystyle \dfrac{5}{16}$
$\displaystyle \dfrac{7}{6}$

13.

Answer.

15.

Answer.

$\displaystyle 0.006,~2.17,~0.0379$
$\displaystyle 0.0379$

17.

Answer.

$6885$ mph

19.

Answer.

$\displaystyle 0$
$\displaystyle \dfrac{-8}{\sqrt{3}}$
$\displaystyle \dfrac{-1}{2}$

21.

Answer.

$\displaystyle (0.5, 0.8)$
$\displaystyle (-0.4,0.9)$
$\displaystyle (-1.0,0.1)$

23.

Answer.

$\displaystyle (r \cos (\alpha), r \sin (\alpha))$
$\displaystyle (-r \cos (\alpha), r \sin (\alpha))$
$\displaystyle (-r \cos (\alpha), -r \sin (\alpha))$
$\displaystyle (r \cos (\alpha), -r \sin (\alpha))$

25.

Answer.

$6\pi$

27.

Answer.

$\gt$

29.

Answer.

$\lt$

31.

Answer.

$9.86$

33.

Answer.

$-1.33$

35.

Answer.

$\displaystyle \dfrac{\pi}{6}$
$\displaystyle \dfrac{\pi}{4}$
$\displaystyle \dfrac{3\pi}{8}$
$\displaystyle \dfrac{5\pi}{12}$

37.

Answer.

$\displaystyle 0.34$
$\displaystyle 0.76$
$\displaystyle 1.25$
$\displaystyle 1.5$

39.

Answer.

$158.2\degree$

41.

Answer.

$graph of cosine and sine$

43.

Answer.

$sinusoidal graph$

mid: $y = 5\text{,}$ amp: $3\text{,}$ period: $\pi$
$sinusoidal curve and horizontal line$

$0.86,~2.28,~4.00,~5.42$

45.

Answer.

$sinusoidal graph$

mid: $y = 10\text{,}$ amp: $4.8\text{,}$ period: $2\pi$
$sinusoidal graph and horizontal line$

$1.93,~4.2$

47.

Answer.

$\dfrac{5\pi}{12},~\dfrac{17\pi}{12}$

49.

Answer.

$\dfrac{\pi}{3},~\dfrac{2\pi}{3}$

51.

Answer.

$\pi$

53.

Answer.

$1.37,~4.51$

55.

Answer.

$6.02,~3.40$

57.

Answer.

$0.32,~5.97$

59.

Answer.

$\displaystyle 1.21,~5.07$
$\displaystyle 0.9394$

61.

Answer.

$\displaystyle 0.40,~2.74$
$\displaystyle 0.3827$

63.

Answer.

$parabola$

Dom: all real numbers, Rge: $y \ge 4$

65.

Answer.

$semicircle$

Dom: $-4 \le s \le 4\text{,}$ Rge: $-4 \le y \le 0$

67.

Answer.

$\displaystyle x^2 + y^2 = 1$
$\displaystyle (\cos (t), \sin (t))$
$\displaystyle \cos^2 (t) + \sin^2 (t) = 1$
Yes

7 Circular Functions
7.1 Transformations of Graphs
Homework 7-1

1.

Answer.

amplitude $2\text{,}$ period $2\pi\text{,}$ midline $y=-3$

3.

Answer.

amplitude $1\text{,}$ period $\dfrac{\pi}{2}\text{,}$ midline $y=0$

5.

Answer.

amplitude $5\text{,}$ period $6\pi\text{,}$ midline $y=0$

7.

Answer.

amplitude $1\text{,}$ period $2\text{,}$ midline $y=1$

9.

Answer.

$transformations of sine graph$

11.

Answer.

$transformations of cosine$

13.

Answer.

$transformations of sine$

15.

Answer.

$cosine transformations$

17.

Answer.

$y=-2\sin (x)$

19.

Answer.

$y=-2\cos (x)$

21.

Answer.

$y=-0.75\cos (x)$

23.

Answer.

amplitude $2\text{,}$ period $\dfrac{2\pi}{3}\text{,}$ midline $y=0$
$\displaystyle y=-2\sin (3x)$

25.

Answer.

amplitude $3\text{,}$ period $2\pi\text{,}$ midline $y=0$
$\displaystyle y=3\sin \left(\dfrac{x}{2}\right)$

27.

Answer.

amplitude $0.5\text{,}$ period $4\pi\text{,}$ midline $y=3.5$
$\displaystyle y=0.5\cos \left(\dfrac{x}{2}\right)+3.5$

29.

Answer.

amplitude $2\text{,}$ period $4\text{,}$ midline $y=-1$
$\displaystyle y=-1+2\sin \left(\dfrac{\pi x}{2}\right)$

31.

Answer.

$t$	$2t$	$\cos (2t)$	$-5\cos (2t)$	$2-5\cos (2t)$
$0$	$0$	$1$	$-5$	$-3$
$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$0$	$0$	$2$
$\dfrac{\pi}{2}$	$\pi$	$-1$	$5$	$7$
$\dfrac{3\pi}{4}$	$\dfrac{3\pi}{2}$	$0$	$0$	$2$
$\pi$	$2\pi$	$1$	$-5$	$-3$

$sinusoidal graph$

33.

Answer.

$t$	$\dfrac{t}{2}$	$\cos \left(\dfrac{t}{2}\right)$	$3\cos \left(\dfrac{t}{2}\right)$	$1+3\cos \left(\dfrac{t}{2}\right)$
$0$	$0$	$1$	$3$	$4$
$\pi$	$\dfrac{\pi}{2}$	$0$	$0$	$1$
$2\pi$	$\pi$	$-1$	$-3$	$-2$
$3\pi$	$\dfrac{3\pi}{2}$	$0$	$0$	$1$
$4\pi$	$2\pi$	$1$	$3$	$4$

$sinusoidal graph$

35.

Answer.

$t$	$\dfrac{t}{3}$	$\sin \left(\dfrac{t}{3}\right)$	$2\sin \left(\dfrac{t}{3}\right)$	$-3+2\sin \left(\dfrac{t}{3}\right)$
$0$	$0$	$0$	$0$	$-3$
$\dfrac{3\pi}{2}$	$\dfrac{\pi}{2}$	$1$	$2$	$-1$
$3\pi$	$\pi$	$0$	$0$	$-3$
$\dfrac{9\pi}{2}$	$\dfrac{3\pi}{2}$	$-1$	$-2$	$-5$
$6\pi$	$2\pi$	$0$	$0$	$-3$

$sinusoidal graph$

37.

Answer.

$sinusoidal graph$

39.

Answer.

$sinusoidal graph$

41.

Answer.

$sinusoidal graph$

43.

Answer.

$sinusoidal graph$

45.

Answer.

$sinusoidal graph$
$\displaystyle W(t)=12+8\cos \left(\dfrac{\pi t}{6}\right)$

47.

Answer.

$sinusoidal graph$
$\displaystyle h=10+14\cos \left(\dfrac{\pi t}{5}\right)$

49.

Answer.

$H=12-2.4\cos \left(\dfrac{\pi t}{6}\right)$

51.

Answer.

$y=155\cos(120 \pi t)$

53.

Answer.

$x$ $\dfrac{-\pi}{4}$ $\dfrac{-\pi}{8}$ $0$ $\dfrac{\pi}{8}$ $\dfrac{\pi}{4}$

$\tan 2x$ undef $-1$ $0$ $1$ undef

$transformed tangent function$
period $\dfrac{\pi}{2}\text{,}$ midline $y=0$

55.

Answer.

$x$ $\dfrac{-\pi}{6}$ $\dfrac{-\pi}{12}$ $0$ $\dfrac{\pi}{12}$ $\dfrac{\pi}{6}$

$4+2\tan 3x$ undef $2$ $0$ $6$ undef

$transformed tangent graph$
period $\dfrac{\pi}{3}\text{,}$ midline $y=4$

57.

Answer.

$x$ $-2\pi$ $-\pi$ $0$ $\pi$ $2\pi$

$3-\tan \left(\dfrac{x}{4}\right)$ undef $4$ $0$ $2$ undef

$transformed tangent graph$
period $4\pi\text{,}$ midline $y=3$

59.

Answer.

$\dfrac{\pi}{12}\text{,}$ $~\dfrac{5\pi}{12}\text{,}$ $~\dfrac{7\pi}{12}\text{,}$ $~\dfrac{11\pi}{12}\text{,}$ $~\dfrac{13\pi}{12}\text{,}$ $~\dfrac{17\pi}{12}\text{,}$ $~\dfrac{19\pi}{12}\text{,}$ $~\dfrac{23\pi}{12}$

61.

Answer.

$\dfrac{7\pi}{12}\text{,}$ $~\dfrac{11\pi}{12}\text{,}$ $~\dfrac{19\pi}{12}\text{,}$ $~\dfrac{23\pi}{12}$

63.

Answer.

$\dfrac{\pi}{12}\text{,}$ $~\dfrac{5\pi}{12}\text{,}$ $~\dfrac{3\pi}{4}\text{,}$ $~\dfrac{13\pi}{12}\text{,}$ $~\dfrac{17\pi}{12}\text{,}$ $~\dfrac{7\pi}{4}$

65.

Answer.

$1.83,~2.88,~4.97,~6.02$

67.

Answer.

$4.19$

69.

Answer.

$0.28,~1.81,~2.37,~3.91,~4.47,~6.00$

7.2 The General Sinusoidal Function
Homework 7-2

1.

Answer.

\(x\)
\(-\pi\)
\(\dfrac{-5\pi}{6}\)
\(\dfrac{-2\pi}{3}\)
\(\dfrac{-\pi}{2}\)
\(\dfrac{-\pi}{3}\)
\(\dfrac{-\pi}{6}\)
\(0\)
\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{2}\)
\(\dfrac{2\pi}{3}\)
\(\dfrac{5\pi}{6}\)
\(\pi\)

\(f(x)\)
\(0\)
\(\dfrac{-1}{2}\)
\(\dfrac{-\sqrt{3}}{2}\)
\(-1\)
\(\dfrac{-\sqrt{3}}{2}\)
\(\dfrac{-1}{2}\)
\(0\)
\(\dfrac{1}{2}\)
\(\dfrac{\sqrt{3}}{2}\)
\(1\)
\(\dfrac{\sqrt{3}}{2}\)
\(\dfrac{1}{2}\)
\(0\)

\(g(x)\)
\(\dfrac{\sqrt{3}}{2}\)
\(\dfrac{1}{2}\)
\(0\)
\(\dfrac{-1}{2}\)
\(\dfrac{-\sqrt{3}}{2}\)
\(-1\)
\(\dfrac{-\sqrt{3}}{2}\)
\(\dfrac{-1}{2}\)
\(0\)
\(\dfrac{1}{2}\)
\(\dfrac{\sqrt{3}}{2}\)
\(1\)
\(\dfrac{\sqrt{3}}{2}\)

$sine and translated sine$
$\dfrac{\pi}{3}$ to the right
$\displaystyle \dfrac{5\pi}{6}$
$\displaystyle \dfrac{-2\pi}{3},~\dfrac{\pi}{3}$

3.

Answer.

$x$	$-\pi$	$\dfrac{-3\pi}{4}$	$\dfrac{-\pi}{2}$	$\dfrac{-\pi}{4}$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$
$f(x)$	$0$	$1$	undef	$-1$	$0$	$1$	undef	$-1$	$0$
$g(x)$	$1$	undef	$-1$	$0$	$1$	undef	$-1$	$0$	$1$

$translated tangent function$
$\dfrac{\pi}{4}$ to the left
$\displaystyle -\pi,~ 0,~ \pi$
$\displaystyle \dfrac{-\pi}{4},~\dfrac{-3\pi}{4}$

5.

Answer.

amplitude 2, shift $\dfrac{\pi}{6}$ to the left

$x$	$x+\dfrac{\pi}{6}$	$\cos\left(x+\dfrac{\pi}{6}\right) $	$-2\cos\left(x+\dfrac{\pi}{6}\right)$
$\dfrac{-7\pi}{6}$	$-\pi$	$-1$	$2$
$\dfrac{-2\pi}{3}$	$\dfrac{-\pi}{2}$	$0$	$0$
$\dfrac{-\pi}{6}$	$0$	$1$	$-2$
$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$0$	$0$
$\dfrac{5\pi}{6}$	$\pi$	$-1$	$2$
$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$0$	$0$
$\dfrac{11\pi}{6}$	$2\pi$	$1$	$-2$

$sinusoidal graph$
$\displaystyle \dfrac{\pi}{2},~ \dfrac{7\pi}{6}$
$\displaystyle \dfrac{\pi}{3},~ \dfrac{4\pi}{3}$

7.

Answer.

$\displaystyle f(x)=\sin \left(x+\dfrac{\pi}{4}\right)$
$\displaystyle f(x)=\cos \left(x-\dfrac{\pi}{4}\right)$

9.

Answer.

$\displaystyle f(x)=\tan \left(x-\dfrac{\pi}{3}\right)$
$\displaystyle f(x)=\tan \left(x+\dfrac{2\pi}{3}\right)$

11.

Answer.

period $\pi\text{,}$ shift $\dfrac{\pi}{6}$ to the right

$x$	$2x$	$2x-\dfrac{\pi}{3} $	$\cos\left(2x-\dfrac{\pi}{3}\right)$
$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$0$	$1$
$\dfrac{5\pi}{12}$	$\dfrac{5\pi}{6}$	$\dfrac{\pi}{2}$	$0$
$\dfrac{2\pi}{3}$	$\dfrac{4\pi}{3}$	$\pi$	$-1$
$\dfrac{11\pi}{12}$	$\dfrac{11\pi}{6}$	$\dfrac{3\pi}{2}$	$0$
$\dfrac{7\pi}{6}$	$\dfrac{7\pi}{3}$	$2\pi$	$1$

$sinusoidal graph$
$\displaystyle \dfrac{\pi}{6},~ \dfrac{7\pi}{6}$
$\displaystyle \dfrac{5\pi}{12},~ \dfrac{11\pi}{12},~ \dfrac{13\pi}{6},~ \dfrac{23\pi}{12}$

13.

Answer.

period 2, shift $\dfrac{1}{3}$ to the left

$x$	$\pi x$	$\pi x+\dfrac{\pi}{3} $	$\sin\left(\pi x+\dfrac{\pi}{3}\right)$
$\dfrac{-1}{3}$	$\dfrac{-\pi}{3}$	$0$	$0$
$\dfrac{1}{6}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{2}$	$1$
$\dfrac{2}{3}$	$\dfrac{2\pi}{3}$	$\pi$	$0$
$\dfrac{7}{6}$	$\dfrac{7\pi}{6}$	$\dfrac{3\pi}{2}$	$-1$
$\dfrac{5}{3}$	$\dfrac{5\pi}{3}$	$2\pi$	$0$

$sinusoidal graph$
$\displaystyle \dfrac{-11}{6},~ \dfrac{1}{6}$
$\displaystyle \dfrac{-4}{3},~ \dfrac{-1}{3},~ \dfrac{2}{3},~ \dfrac{5}{3}$

15.

Answer.

midline $y=4\text{,}$ period $4\pi\text{,}$ horizontal shift $\dfrac{\pi}{3}$ to the right, amplitude 3

$x$	$\dfrac{x}{2}$	$\dfrac{x}{2}-\dfrac{\pi}{6} $	$\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)$	$3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4$
$\dfrac{\pi}{3}$	$\dfrac{\pi}{6}$	$0$	$0$	$4$
$\dfrac{4\pi}{3}$	$\dfrac{2\pi}{3}$	$\dfrac{\pi}{2}$	$1$	$7$
$\dfrac{7\pi}{3}$	$\dfrac{7\pi}{6}$	$\pi$	$0$	$3$
$\dfrac{10\pi}{3}$	$\dfrac{5\pi}{3}$	$\dfrac{3\pi}{2}$	$-1$	$1$
$\dfrac{13\pi}{3}$	$\dfrac{13\pi}{6}$	$2\pi$	$0$	$4$

$sinusoidal graph$
no solution for $0 \le x \le 2\pi$
$\displaystyle \dfrac{\pi}{3}$

17.

Answer.

$y=2\sin\left(\dfrac{2\pi}{3}(x+4)\right)+5$

$sinusoidal graph$

19.

Answer.

$y=-5\cos\left(\dfrac{\pi x}{180}\right)+12$

$sinusoidal graph$

21.

Answer.

$\displaystyle f(x)=3\sin \left(x+\dfrac{2\pi}{3}\right)$
$\displaystyle f(x)=3\cos \left(x+\dfrac{\pi}{6}\right)$

23.

Answer.

$\displaystyle f(x)=2\sin (2(x-\dfrac{\pi}{4}))$
$\displaystyle f(x)=-2\cos (2x)$

25.

Answer.

$\displaystyle f(x)=4\sin \left[\dfrac{1}{4}\left(x-\dfrac{7\pi}{3}\right)\right]$
$\displaystyle f(x)=-4\cos \left[\dfrac{1}{4}\left(x-\dfrac{\pi}{3}\right)\right]$

27.

Answer.

midline $T=35.35\text{,}$ period 12, amplitude 36.95
$\displaystyle T(m)=-36.95 \cos \left(\dfrac{\pi}{6} m\right)+35.35$
$sinusoidal graph$

29.

Answer.

midline $h=1.4\text{,}$ period $\dfrac{2 \pi}{0.51} \approx{12.32}\text{,}$ amplitude 1.4
$sinusoidal graph$
high 11:10 am, low 5:19 pm

31.

Answer.

amplitude 3.2, period 2, midline $y=2$
$\displaystyle f(t)=2+3.2\cos (\pi t)$

33.

Answer.

amplitude 5, period 1, midline $y=0$
$\displaystyle H(x)=5\sin (2\pi x) + 5$

7.3 Solving Equations
Homework 7-3

1.

Answer.

$\dfrac{3\pi}{8}\text{,}$ $~ \dfrac{7\pi}{8}\text{,}$ $~ \dfrac{11\pi}{8}\text{,}$ $~ \dfrac{15\pi}{8}$

3.

Answer.

$0\text{,}$ $~ \dfrac{\pi}{2}\text{,}$ $~ \pi\text{,}$ $~ \dfrac{3\pi}{2}\text{,}$ $~ 2\pi$

5.

Answer.

$\dfrac{2\pi}{9}\text{,}$ $~ \dfrac{4\pi}{9}\text{,}$ $~ \dfrac{8\pi}{9}\text{,}$ $~ \dfrac{10\pi}{9}\text{,}$ $~ \dfrac{14\pi}{9}\text{,}$ $~ \dfrac{16\pi}{9}$

7.

Answer.

$\dfrac{\pi}{12}\text{,}$ $~ \dfrac{5\pi}{12}\text{,}$ $~ \dfrac{13\pi}{12}\text{,}$ $~ \dfrac{17\pi}{12}$

9.

Answer.

$\dfrac{\pi}{18}\text{,}$ $~ \dfrac{7\pi}{18}\text{,}$ $~ \dfrac{13\pi}{18}\text{,}$ $~ \dfrac{19\pi}{18}\text{,}$ $~ \dfrac{25\pi}{18}\text{,}$ $~ \dfrac{31\pi}{18}$

11.

Answer.

$0.491,~ 2.651,~ 3.632,~ 5.792$

13.

Answer.

$0.540\text{,}$ $~ 1.325\text{,}$ $~ 2.110\text{,}$ $~ 2.896\text{,}$ $~ 3.681\text{,}$ $~ 4.467\text{,}$ $~ 5.252\text{,}$ $~ 6.037$

15.

Answer.

$1.114\text{,}$ $~ 2.027\text{,}$ $~ 3.209\text{,}$ $~ 4.122\text{,}$ $~ 5.303\text{,}$ $~ 6.216$

17.

Answer.

$0.702\text{,}$ $~ 2.440\text{,}$ $~ 3.843\text{,}$ $~ 5.582$

19.

Answer.

$0\text{,}$ $~ 1\text{,}$ $~ 2\text{,}$ $~ 3\text{,}$ $~ 4\text{,}$ $~ 5\text{,}$ $~ 6$

21.

Answer.

$\dfrac{\pi}{6}\text{,}$ $~ \dfrac{2\pi}{3}\text{,}$ $~ \dfrac{7\pi}{6}\text{,}$ $~ \dfrac{5\pi}{3}$

23.

Answer.

$\dfrac{5\pi}{12}\text{,}$ $~ \dfrac{7\pi}{12}\text{,}$ $~ \dfrac{13\pi}{12}\text{,}$ $~ \dfrac{5\pi}{4}\text{,}$ $~ \dfrac{7\pi}{4}\text{,}$ $~ \dfrac{23\pi}{12}$

25.

Answer.

$\dfrac{3\pi}{2}$

27.

Answer.

$\dfrac{7}{6}\text{,}$ $~ \dfrac{11}{6}\text{,}$ $~ \dfrac{19}{6}\text{,}$ $~ \dfrac{23}{6}\text{,}$ $~ \dfrac{31}{6}\text{,}$ $~ \dfrac{35}{6}$

29.

Answer.

$1.14\text{,}$ $~ 1.62\text{,}$ $~ 3.23\text{,}$ $~ 3.72\text{,}$ $~ 5.24\text{,}$ $~ 5.81$

31.

Answer.

$0.44\text{,}$ $~ 1.44\text{,}$ $~ 2.44\text{,}$ $~ 3.44\text{,}$ $~ 4.44\text{,}$ $~ 5.44$

33.

Answer.

$0.01\text{,}$ $~ 3.39\text{,}$ $~ 6.01$

35.

Answer.

$0.564\text{,}$ $~ 1.182\text{,}$ $~ 2.658\text{,}$ $~ 3.276\text{,}$ $~ 4.752\text{,}$ $~ 5.371$

37.

Answer.

$0.423\text{,}$ $~ 2.977\text{,}$ $~ 4.423$

39.

Answer.

$1.165,~ 4.165$

41.

Answer.

$2.251$

43.

Answer.

$\displaystyle P(t)=4000\cos\left(\dfrac{\pi}{6}t\right)+46,000$
$t=\cos^{-1}\left( \dfrac{-1}{4} \right)\cdot\dfrac{6}{\pi}\approx3.48$ months (Dec) or $t=12-\cos^{-1}\left( \frac{-1}{4} \right)\cdot\frac{6}{\pi}\approx 8.52$ months (June)
$sinusoidal graph$

$P(t)$ is less than 45,000 between $A$ and $B\text{.}$

45.

Answer.

$\displaystyle h(t)=11-10\cos\left(\dfrac{\pi}{30}t\right)$
$t=\cos\left(-0.7 \right)\cdot \dfrac{30}{\pi}\approx 22.40$ sec or $t=60-\cos\left(-0.7 \right)\cdot \dfrac{30}{\pi}\approx 37.60$ sec
$sinusoidal graph$

Delbert is above 18 m between $A$ and $B\text{.}$

7.4 Chapter 7 Summary and Review
Review Problems

1.

Answer.

amp: $2\text{,}$ period: $\dfrac{2\pi}{3} \text{;}$ mid: $y=4$

3.

Answer.

amp: $2.5\text{,}$ period: $2\text{;}$ mid: $y=-2$

5.

Answer.

$sinusoidal graph$

7.

Answer.

$sinusoidal graph$

9.

Answer.

$y=3+2\sin (x) $

11.

Answer.

$y=4-3\sin \left(\dfrac{x}{4}\right) $

13.

Answer.

period: $4\pi\text{,}$ shift: $\dfrac{\pi}{3}$ left

$x$	$\dfrac{x}{2}$	$\dfrac{x}{2}+\dfrac{\pi}{6} $	$\sin\left(\dfrac{x}{2}+\dfrac{\pi}{6}\right)$
$\dfrac{-2\pi}{3}$	$\dfrac{\pi}{3}$	$\dfrac{-\pi}{6}$	$\dfrac{-1}{2}$
$\dfrac{-\pi}{3}$	$\dfrac{-\pi}{6}$	$0$	$0$
$0$	$0$	$\dfrac{\pi}{6}$	$\dfrac{1}{2}$
$\dfrac{\pi}{6}$	$\dfrac{\pi}{12}$	$\dfrac{\pi}{4}$	$\dfrac{1}{\sqrt{2}}$
$\dfrac{\pi}{3}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\sqrt{3}}{2}$
$\dfrac{2\pi}{3}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$1$
$\pi$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{\sqrt{3}}{2}$

$sinusoidal graph$
$\displaystyle \dfrac{2\pi}{3} $
$\displaystyle \dfrac{-\pi}{3} $

15.

Answer.

mid: $y=20\text{,}$ period: 0, amp: 5

Fill in the table of values.

$x$	$\dfrac{\pi}{30}x $	$\cos\left(\dfrac{\pi}{30}x\right)$	$20-5\cos\left(\dfrac{\pi}{30}x\right)$
$-5$	$\dfrac{-\pi}{6}$	$\dfrac{\sqrt{3}}{2}$	$20-\dfrac{\sqrt{3}}{2}$
$0$	$0$	$1$	$15$
$5$	$\dfrac{\pi}{6}$	$\dfrac{\sqrt{3}}{2}$	$20-\dfrac{\sqrt{3}}{2}$
$10$	$\dfrac{\pi}{3}$	$\dfrac{1}{2}$	$17.5$
$15$	$\dfrac{\pi}{2}$	$0$	$20$
$50$	$\pi$	$-1$	$25$

$sinusoidal graph$
30
15, 45

17.

Answer.

$sinusoidal graph$

19.

Answer.

$sinusoidal graph$
0.57, 3.07, 3.71

21.

Answer.

$y=85.5-19.5\cos\left(\dfrac{\pi}{6}t\right) $

23.

Answer.

amp: 3, period: 12, midline: $y=15$
$\displaystyle y=15-3\cos\left(\frac{\pi}{6}t\right) $

25.

Answer.

$\dfrac{7\pi}{12}\text{,}$ $\dfrac{11\pi}{12}\text{,}$ $\dfrac{19\pi}{12}\text{,}$ $\dfrac{23\pi}{12}$

27.

Answer.

$0\text{,}$ $\dfrac{\pi}{4}\text{,}$ $\dfrac{\pi}{2}\text{,}$ $\dfrac{3\pi}{4}\text{,}$ $\pi\text{,}$ $\dfrac{5\pi}{4}\text{,}$ $\dfrac{7\pi}{4}\text{,}$ $2\pi$

29.

Answer.

0.066, 1.113, 2.160, 3.207, 4.255, 5.302

31.

Answer.

1.150, 1.991, 4.292, 5.133

33.

Answer.

$\dfrac{\pi}{24} \text{,}$ $\dfrac{5\pi}{24} \text{,}$ $\dfrac{25\pi}{24} \text{,}$ $\dfrac{29\pi}{24} $

35.

Answer.

No solution

37.

Answer.

0.375, 1.422, 2.470, 3.517, 4.564, 5.611

39.

Answer.

2.120, 4.880

8 More Functions and Identities
8.1 Sum and Difference Formulas
Homework 8-1

1.

Answer.

$angles$

$x_2=x_1\text{,}$ $y_2=-y_1\text{,}$ and $r_2=r_1\text{.}$ Thus, $\cos(-\alpha)=\dfrac{x_2}{r_2} =\dfrac{x_1}{r_1}=\cos(\alpha) \text{,}$ $\sin(-\alpha)=\dfrac{y_2}{r_2} =\dfrac{-y_1}{r_1}=-\sin(\alpha) \text{,}$ and $\tan(-\alpha)=\dfrac{y_2}{x_2} =\dfrac{-y_1}{x_1}=-\tan(\alpha) \text{.}$

3.

Answer.

$\dfrac{-(\sqrt{2} + \sqrt{6})}{4}$

$angles$

5.

Answer.

$\cos(0.3-2x)=0.24\text{,}$ $\sin(0.3-2x)=0.97$

7.

Answer.

$\cos(45\degree + 45\degree)=\cos(90\degree)=0\text{,}$ but $\cos (45\degree) +\cos (45\degree) = \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2} $

9.

Answer.

$\tan(87\degree -29\degree)\approx 1.600\text{,}$ but $\tan (87\degree) -\tan (29\degree) \approx 18.527 $

11.

Answer.

$two sinusoidal graphs$

The curves are different.

13.

Answer.

$\displaystyle \dfrac{63}{65} $
$\displaystyle \dfrac{-16}{65} $
$\displaystyle \dfrac{-16}{63} $

15.

Answer.

$\displaystyle \dfrac{44}{117} $
$\displaystyle \dfrac{4}{3} $

17.

Answer.

$\displaystyle \dfrac{36}{85} $
$\displaystyle \dfrac{-13}{84} $

19.

Answer.

$\displaystyle \dfrac{-16}{65} $
$\displaystyle \dfrac{63}{65} $
$\displaystyle \dfrac{-16}{63} $
$angles$

21.

Answer.

$\cos (15\degree)=\dfrac{\sqrt{6}+\sqrt{2}}{4} \text{,}$ $\tan (15\degree) = 2-\sqrt{3}$

23.

Answer.

$\dfrac{6\sqrt{2}+1}{10}$

25.

Answer.

$\cos (\theta)$

27.

Answer.

$\dfrac{\sqrt{3}}{2}\cos (t) -\dfrac{1}{2}\sin (t) $

29.

Answer.

$\dfrac{\sqrt{3}\tan\beta -1}{\sqrt{3}+\tan\beta} $

31.

Answer.

33.

Answer.

35.

Answer.

$1=2\left(\dfrac{1}{\sqrt{2}} \right)\left(\dfrac{1}{\sqrt{2}} \right) $

37.

Answer.

$\frac{1}{2} =\left(\dfrac{\sqrt{3}}{2} \right)^2 - \left(\dfrac{1}{2} \right)^2 $

39.

Answer.

False, but $\cos (2\alpha)=2(0.32)^2-1 $

41.

Answer.

False, but $2\theta = \sin^{-1}(h) $

43.

Answer.

$\sin (68\degree)$

45.

Answer.

$\cos\left(\dfrac{\pi}{8}\right) $

47.

Answer.

$\cos (6\theta)$

49.

Answer.

$\sin 10t$

51.

Answer.

$\tan 128\degree$

53.

Answer.

$\cos (4\beta)$

55.

Answer.

$\displaystyle \dfrac{5}{6} $
$\displaystyle \dfrac{\sqrt{11}}{6} $
$\displaystyle \dfrac{5}{\sqrt{11}} $
$\displaystyle \dfrac{5\sqrt{11}}{18} $
$\displaystyle \dfrac{-7}{18} $
$\displaystyle \dfrac{-5\sqrt{11}}{7} $

57.

Answer.

$\displaystyle \dfrac{1}{\sqrt{w^2+1}} $
$\displaystyle \dfrac{w}{\sqrt{w^2+1}} $
$\displaystyle \dfrac{1}{w} $
$\displaystyle \dfrac{2w}{w^2+1} $
$\displaystyle \dfrac{w^2 -1}{w^2+1} $
$\displaystyle \dfrac{2w}{w^2-1} $

59.

Answer.

$\displaystyle \dfrac{-5}{13} $
$\displaystyle \dfrac{-120}{169} $
$\displaystyle \dfrac{119}{169} $
$\displaystyle \dfrac{-120}{119} $
$angles$

61.

Answer.

$\displaystyle \dfrac{8}{15} $
$\displaystyle \dfrac{-15}{17} $
$\displaystyle \dfrac{-8}{17} $

63.

Answer.

$\displaystyle 2\sin(\theta) \cdot \cos(\theta) +\sqrt{2}\cos(\theta)=0 $
$\dfrac{\pi}{2} \text{,}$ $\dfrac{5\pi}{4} \text{,}$ $\dfrac{3\pi}{2} \text{,}$ $\dfrac{7\pi}{4} $

65.

Answer.

$\displaystyle 2\cos^2 (t) -5\cos (t) +2=0 $
$\dfrac{\pi}{3} \text{,}$ $\dfrac{5\pi}{3} $

67.

Answer.

$\displaystyle \frac{2\tan(\beta)}{1-\tan^2(\beta)}+2\sin(\beta)=0 $
$0\text{,}$ $\dfrac{\pi}{3}\text{,}$ $\pi$ , $\dfrac{5\pi}{3} $

69.

Answer.

$\displaystyle 3\cos(\phi) - \cos (\phi)=\sqrt{3} $
$\dfrac{\pi}{6}\text{,}$ $\dfrac{11\pi}{6} $

71.

Answer.

$\displaystyle \sin (3\phi) =1$
$\dfrac{\pi}{6}$ , $\dfrac{5\pi}{6}$ , $\dfrac{3\pi}{2} $

73.

Answer.

$\displaystyle \cos (\theta + 90\degree)=-\sin\theta $
$\displaystyle \sin (\theta + 90\degree)=\cos\theta$

75.

Answer.

$\displaystyle \cos \left(\dfrac{\pi}{2} -\theta\right) = \cos\frac{\pi}{2} \cos(\theta) + \sin \frac{\pi}{2}\sin\theta = \sin (\theta)$
$\displaystyle \sin \left(\dfrac{\pi}{2} -\theta\right) = \sin\frac{\pi}{2} \cos(\theta) - \cos \frac{\pi}{2}\sin(\theta)= \cos (\theta)$

77.

Answer.

$\begin{aligned}[t]\sin(2\theta) \amp=\sin(\theta + \theta)\\ \amp= \sin(\theta)\cos(\theta) + \sin(\theta)\cos(\theta) \\ \amp= 2\sin(\theta)\cos(\theta) \end{aligned}$

79.

Answer.

Not an identity.
$\beta=\pi$ (many answers possible)

81.

Answer.

Identity

83.

Answer.

Not an identity.
$\theta=0$ (many answers possible)

85.

Answer.

Identity

87.

Answer.

Identity

89.

Answer.

$triangle inscribed in rectangle$

$\displaystyle l_1=\sin(\alpha), \, l_2=\cos(\alpha) $
$\theta_1$ and $\beta$ are both complements of $\phi\text{;}$ $\theta_2$ and $\alpha+\beta$ are alternate interior angles
$s_1=\cos(\alpha+\beta) \text{,}$ $s_2=\sin(\alpha+\beta) $
$s_3=\sin(\alpha)\sin(\beta) \text{,}$ $s_4=\sin(\alpha)\cos(\beta) $
$s_5=\cos(\alpha)\cos(\beta) \text{,}$ $s_6=\cos(\alpha)\sin(\beta) $
$\sin(\alpha+\beta) = \sin(\alpha)\cos(\beta) +\cos(\alpha)\sin(\beta) \text{,}$ $\cos(\alpha+\beta) = \cos(\alpha)\cos(\beta) +\sin(\alpha)\sin(\beta) $

91.

Answer.

$\displaystyle (AB)^2=2-2\cos(\alpha-\beta)$
$\displaystyle (AB)^2=(\cos(\alpha)-\cos(\beta))^2 + (\sin(\alpha) - \sin(\beta))^2 $
$\displaystyle \begin{aligned}[t] 2-2\cos(\alpha-\beta)\amp = (\cos(\alpha)-\cos(\beta))^2 + (\sin(\alpha) - \sin(\beta))^2 \\ 2-2\cos(\alpha-\beta)\amp = \cos^2(\alpha) -2\cos(\alpha)\cos(\beta) + \cos^2 (\beta) + \,\\ \amp\hphantom{000000000} +\sin^2 (\alpha) - 2\sin(\alpha)\sin(\beta) + \sin^2(\beta) \\ 2-2\cos(\alpha-\beta)\amp = 1+1 - 2(\cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta)) \\ -2\cos(\alpha-\beta)\amp = -2(\cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta)) \\ \cos(\alpha-\beta)\amp = \cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta)) \end{aligned}$

8.2 Inverse Trigonometric Functions
Homework 8-2

1.

Answer.

No inverse: Some horizontal lines intersect the curve in more than one point.

3.

Answer.

Inverse exists: The function is 1-1.

5.

Answer.

$graph$

No inverse

7.

Answer.

$simicircle$

No inverse

9.

Answer.

$16.5\degree$

11.

Answer.

$46.4\degree$

13.

Answer.

$=51.9\degree$

15.

Answer.

$\dfrac{3\pi}{4} $

17.

Answer.

$\dfrac{-\pi}{6}$

19.

Answer.

$\dfrac{\pi}{6}$

21.

Answer.

$triangle$

$\displaystyle h=500 \tan(\theta)$
$\displaystyle \theta=\tan^{-1}\left(\dfrac{h}{500} \right) $
$\theta=\tan^{-1}(2) \text{,}$ so the angle of elevation is $\tan^{-1} (2)\approx 63.4\degree $ when the rocket is 1000 yd high.

23.

Answer.

$triangle$

$\displaystyle d=\dfrac{50}{\tan\theta}$
$\displaystyle \theta=\tan^{-1}\left(\dfrac{50}{d} \right) $
$\theta=\tan^{-1}(0.25) \text{;}$ the bilboard subtends an angle of $\tan^{-1}(0.25) \approx 14\degree $ at a distance of 200 ft.

25.

Answer.

$triangles$

$\displaystyle \alpha=\tan^{-1}\left(\dfrac{1}{x}\right) $
$\displaystyle \beta=\tan^{-1}\left(\dfrac{5}{x} \right) - \tan^{-1}\left(\dfrac{1}{x}\right) $
$\beta=45\degree - \tan^{-1}\left(\dfrac{1}{5}\right) \text{,}$ so the painting subtends an angle of $45\degree - \tan^{-1}\left(\dfrac{1}{5}\right) \approx 33.7\degree $ when Martin is 5 meters from the wall.

27.

Answer.

$t=\dfrac{1}{2\pi\omega}\left( \sin^{-1}\dfrac{V}{V_0}-\phi \right) $

29.

Answer.

$A=\sin^{-1}\left(\dfrac{a\sin (B)}{b} \right) $

31.

Answer.

$\theta= \pm \cos^{-1}\left(\dfrac{k}{PR^4} \right) $

33.

Answer.

$\dfrac{2}{\sqrt{5}} $

35.

Answer.

$\dfrac{1}{\sqrt{5}} $

37.

Answer.

$\dfrac{5}{7} $

39.

Answer.

$\dfrac{\sqrt{1-x^2}}{x} $

41.

Answer.

$\sqrt{1-h^2} $

43.

Answer.

$\dfrac{2t}{\sqrt{4t^2+1}} $

45.

Answer.

$x$	$-1$	$\frac{-\sqrt{3}}{2}$	$\frac{-\sqrt{2}}{2}$	$\frac{-1}{2}$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$
$\cos^{-1}(x)$	$\pi$	$\frac{5\pi}{6} $	$\frac{3\pi}{4} $	$\frac{2\pi}{3} $	$\frac{\pi}{2} $	$\frac{\pi}{3} $	$\frac{\pi}{4} $	$\frac{\pi}{6} $	$0 $

$arccosine$

47.

Answer.

$x$	$-\sqrt{3}$	$-1$	$\frac{-1}{\sqrt{3}}$	$0$	$\frac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$
$\cos^{-1}(x)$	$\frac{-\pi}{2} $	$\frac{-\pi}{3} $	$\frac{-\pi}{6} $	$0 $	$\frac{\pi}{6} $	$\frac{\pi}{4} $	$\frac{\pi}{3} $

$arctangent$

49.

Answer.

a–b.

$transformations of arccos$

c. No

51.

Answer.

$arctangent$

c. No

53.

Answer.

$\dfrac{8}{17} $

55.

Answer.

$\dfrac{16}{65} $

57.

Answer.

$\dfrac{4\sqrt{2} }{7} $

59.

Answer.

$\displaystyle \dfrac{-63}{65} $
$\displaystyle \dfrac{16}{65} $
$\displaystyle \dfrac{-33}{65} $
$\displaystyle \dfrac{56}{65} $

61.

Answer.

$1$

63.

Answer.

$\displaystyle \dfrac{2x}{x^2+1} $
$\displaystyle 1-x^2$

65.

Answer.

$\sin (2\theta)= \dfrac{2x\sqrt{25-x^2}}{25} \text{,}$ $\cos (2\theta)= \dfrac{25-2x^2}{25} $

67.

Answer.

$\arctan\left(\dfrac{x}{3}+\dfrac{3x}{2(x^2+9)}\right) $

69.

Answer.

$\displaystyle -1\le x\le 1$
Yes.
All
$x\lt \dfrac{-\pi}{2} $ or $x\gt\dfrac{\pi}{2} $

71.

Answer.

Domain: $-1\le x \le 1\text{,}$ range: $\left\{\dfrac{\pi}{2}\right\} $
Let $\theta=\sin^{-1}(x)\text{.}$ Then $x=\sin(\theta)= \cos\left(\dfrac{\pi}{2} - \theta \right) $ and $\cos^{-1}(x)= \dfrac{\pi}{2} - \theta \text{.}$ So $~\sin^{-1}(x)+\cos^{-1}(x) = \theta + \left(\dfrac{\pi}{2} - \theta\right) = \dfrac{\pi}{2} $ .

73.

Answer.

$\displaystyle \dfrac{\theta}{2} $
$\displaystyle t=\sin(\theta)$
$\displaystyle \frac{1}{2}\arcsin (t) $

8.3 The Reciprocal Functions
Homework 8-3

1.

Answer.

$2.203$

3.

Answer.

$0.466$

5.

Answer.

$5.883$

7.

Answer.

$1.203$

9.

Answer.

$2$

11.

Answer.

$1$

13.

Answer.

$\dfrac{-2\sqrt{3}}{3}$

15.

Answer.

$\sqrt{2}$

17.

Answer.

$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$
$\sec (\theta)$	$1$	$\dfrac{2\sqrt{3}}{3}$	$\sqrt{2}$	$2$	undefined	$-2$	$-\sqrt{2}$	$-\dfrac{2\sqrt{3}}{3}$	$-1$
$\csc (\theta)$	undefined	$2$	$\sqrt{2}$	$\dfrac{2\sqrt{3}}{3}$	$1$	$\dfrac{2\sqrt{3}}{3}$	$\sqrt{2}$	$2$	undefined
$\cot (\theta)$	undefined	$\sqrt{3}$	$1$	$\dfrac{\sqrt{3}}{3}$	$0$	$\dfrac{-\sqrt{3}}{3}$	$-1$	$-\sqrt{3}$	undefined

19.

Answer.

$\displaystyle 0.980$
$\displaystyle 1.020$
$\displaystyle 1.369$
$\displaystyle 1.020$
$\displaystyle 0.284$
$\displaystyle 1.020$

21.

Answer.

$\sin (\theta) = \dfrac{4}{5}\text{,}$ $~\cos (\theta) = \dfrac{3}{5}\text{,}$ $~\tan (\theta) = \dfrac{4}{3}\text{,}$ $~\sec (\theta) = \dfrac{5}{3}\text{,}$ $~\csc (\theta) = \dfrac{5}{4}\text{,}$ $~\cot (\theta) = \dfrac{3}{4}$

23.

Answer.

$\sin (\theta) = \dfrac{4}{\sqrt{41}}\text{,}$ $~\cos (\theta) = \dfrac{5}{\sqrt{41}}\text{,}$ $~\tan (\theta) = \dfrac{4}{5}\text{,}$ $~\sec (\theta) = \dfrac{\sqrt{41}}{5}\text{,}$ $~\csc (\theta) = \dfrac{\sqrt{41}}{4}\text{,}$ $~\cot (\theta) = \dfrac{5}{4}$

25.

Answer.

$\sin (\theta) = \dfrac{5}{\sqrt{74}}\text{,}$ $~\cos (\theta) = \dfrac{-7}{\sqrt{74}}\text{,}$ $~\tan (\theta) = \dfrac{-5}{7}\text{,}$ $~\sec (\theta) = \dfrac{-\sqrt{74}}{7}\text{,}$ $~\csc (\theta) = \dfrac{\sqrt{74}}{5}\text{,}$ $~\cot (\theta) = \dfrac{-7}{5}$

27.

Answer.

$\sin (\theta) = \dfrac{-5}{8}\text{,}$ $~\cos (\theta) = \dfrac{\sqrt{39}}{8}\text{,}$ $~\tan (\theta) = \dfrac{5}{\sqrt{39}}\text{,}$ $~\sec (\theta) = \dfrac{-8}{\sqrt{39}}\text{,}$ $~\csc (\theta) = \dfrac{-8}{5}\text{,}$ $~\cot (\theta) = \dfrac{\sqrt{39}}{5}$

29.

Answer.

$\displaystyle d=h\csc (\theta)$
155.572 miles

31.

Answer.

0.78 sec
$\displaystyle l=8t^2\sin (2\theta)$

33.

Answer.

$\sin (\theta) = \dfrac{7}{\sqrt{x^2+49}}\text{,}$ $~\cos (\theta) = \dfrac{x}{\sqrt{x^2+49}}\text{,}$ $~\tan (\theta) = \dfrac{7}{x}\text{,}$ $~\sec (\theta) = \dfrac{\sqrt{x^2+49}}{x}\text{,}$ $~\csc (\theta) = \dfrac{\sqrt{x^2+49}}{7}\text{,}$ $~\cot (\theta) = \dfrac{x}{7}$

35.

Answer.

$\sin (\theta) = S\text{,}$ $~\cos (\theta) = \sqrt{1-S^2}\text{,}$ $~\tan (\theta) = \dfrac{S}{\sqrt{1-S^2}}\text{,}$ $~\sec (\theta) = \dfrac{1}{\sqrt{1-S^2}}\text{,}$ $~\csc (\theta) = \dfrac{1}{S}\text{,}$ $~\cot (\theta) = \dfrac{\sqrt{1-S^2}}{S}$

37.

Answer.

$\sin (\theta) = \dfrac{-\sqrt{9-a^2}}{3}\text{,}$ $~\cos (\theta) = \dfrac{a}{3}\text{,}$ $~\tan (\theta) = \dfrac{-\sqrt{9-a^2}}{a}\text{,}$ $~\sec (\theta) = \dfrac{3}{a}\text{,}$ $~\csc (\theta) = \dfrac{-3}{\sqrt{9-a^2}}\text{,}$ $~\cot (\theta) = \dfrac{-a}{\sqrt{9-a^2}}$

39.

Answer.

$AC,~OA,~BD,~OD,~OE,~EF$

41.

Answer.

$angle$

$~\sin (\theta) = \dfrac{-\sqrt{3}}{2}\text{,}$ $~\cos (\theta) = \dfrac{1}{2}\text{,}$ $~\tan (\theta) = -\sqrt{3}\text{,}$ $~\sec (\theta) = 2\text{,}$ $~\csc (\theta) = \dfrac{-2\sqrt{3}}{3}\text{,}$ $~\cot (\theta) = \dfrac{-\sqrt{3}}{3}$

43.

Answer.

$triangle$

$\sin (\alpha) = \dfrac{1}{3}\text{,}$ $~\cos (\alpha) = \dfrac{2\sqrt{2}}{3}\text{,}$ $~\tan (\alpha) = \dfrac{\sqrt{2}}{4}\text{,}$ $~\sec (\alpha) = \dfrac{3\sqrt{2}}{4}\text{,}$ $~\csc (\alpha) = 3\text{,}$ $~\cot (\alpha) = 2\sqrt{2}$

45.

Answer.

$angle$

$\sin (\gamma) = \dfrac{-4}{\sqrt{17}}\text{,}$ $\cos (\gamma) = \dfrac{-1}{\sqrt{17}}\text{,}$ $\tan (\gamma) = 4\text{,}$ $\sec (\gamma) = -\sqrt{17}\text{,}$ $\csc (\gamma) = \dfrac{-\sqrt{17}}{4}\text{,}$ $\cot (\gamma) = \dfrac{1}{4}$

47.

Answer.

$\dfrac{4\sqrt{3}}{3}+2\sqrt{2}$

49.

Answer.

$\dfrac{\sqrt{3}}{3}$

51.

Answer.

$\dfrac{4\sqrt{6}}{3}+\dfrac{10}{3}$

53.

Answer.

$x$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$\sec (x)$	$1$	$\sqrt{2}$	undefined	$-\sqrt{2}$	$-1$	$-\sqrt{2}$	undefined	$\sqrt{2}$	$1$

$secant$

55.

Answer.

$sine and cosecant$

57.

Answer.

$x$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$\cot (x)$	undefined	$1$	$0$	$-1$	undefined	$1$	$0$	$-1$	undefined

$cotangent$

59.

Answer.

$\begin{aligned}[t]\dfrac{\csc (x)}{\cot (x)} \amp=\dfrac{\dfrac{1}{\sin (x)}}{\dfrac{\cos (x)}{\sin (x)}}\\ \amp= \dfrac{1}{\sin (x)}\div \dfrac{\cos (x)}{\sin (x)} \\ \amp= \dfrac{1}{\sin (x)}\cdot \dfrac{\sin (x)}{\cos (x)} \\ \amp= \dfrac{1}{\cos (x)} \\ \amp= \sec (x)\end{aligned}$

61.

Answer.

$\dfrac{\sec (x) \cot (x)}{\csc (x)}=\dfrac{\dfrac{1}{\cos (x)} \cdot \dfrac{\cos (x)}{\sin (x)}}{\dfrac{1}{\sin (x)}} = \dfrac{\dfrac{1}{\sin (x)}}{\dfrac{1}{\sin (x)}} = 1$

63.

Answer.

$\tan (x) \csc (x) = \dfrac{\sin (x)}{\cos (x)} \cdot \dfrac{1}{\sin (x)} = \dfrac{1}{\cos (x)} = \sec (x)$

65.

Answer.

$\dfrac{\pi}{6},~ \dfrac{5\pi}{6}$

67.

Answer.

$\dfrac{3\pi}{4},~ \dfrac{5\pi}{4}$

69.

Answer.

$\dfrac{5\pi}{6},~ \dfrac{11\pi}{6}$

71.

Answer.

$\dfrac{-\sqrt{5}}{5}$

73.

Answer.

$\dfrac{\sqrt{a^2-4}}{2}$

75.

Answer.

$\dfrac{\sqrt{w^2-1}}{-w}$

77.

Answer.

$\sec (s) = \dfrac{-5}{4}\text{,}$ $~\csc (s) = \dfrac{5}{3}\text{,}$ $~\cot (s) = \dfrac{-4}{3}$

79.

Answer.

$\sec (s) = \dfrac{1}{\sqrt{1-w^2}}\text{,}$ $~\csc (s) = \dfrac{1}{w}\text{,}$ $~\cot (s) = \dfrac{\sqrt{1-w^2}}{w}$

81.

Answer.

$\dfrac{\sin (\theta)}{\cos^2(\theta)}$

83.

Answer.

$\sec (t)$

85.

Answer.

$\dfrac{1-\sin (\beta)}{\cos (\beta)}$

87.

Answer.

$-\cos (x)$

89.

Answer.

$\begin{aligned}[t] \cos^2 (\theta) + \sin^2 (\theta) \amp = 1\\ \dfrac{\cos^2 (\theta)}{\cos^2 (\theta)}+\dfrac{\sin^2 (\theta)}{\cos^2 (\theta)}\amp = \dfrac{1}{\cos^2 (\theta)}\\ 1 + \tan^2 (\theta) \amp = \sec^2 (\theta) \end{aligned}$

91.

Answer.

$\displaystyle \csc (\theta) = -\sqrt{26}$
$\displaystyle \sin (\theta) = \dfrac{-\sqrt{26}}{26},~\cos (\theta) = \dfrac{-5\sqrt{26}}{26},~\tan (\theta) = \dfrac{1}{5},~\sec (\theta) = \dfrac{-\sqrt{26}}{5}$

93.

Answer.

$\cos (t) = \pm \sqrt{1-\sin^2 (t)}\text{,}$ $~\tan (t) = \dfrac{\pm \sin (t)}{\sqrt{1-\sin^2 (t)}}\text{,}$ $~\sec (t) = \dfrac{\pm 1}{\sqrt{1-\sin^2 (t)}}\text{,}$ $~\csc (t) = \dfrac{1}{\sin (t)}\text{,}$ $~ \cot (t) = \dfrac{\pm \sqrt{1-\sin^2 (t)}}{\sin (t)}$

95.

Answer.

$\begin{aligned}[t] \dfrac{a}{\sin (A)} \amp = \dfrac{b}{\sin (B)} = \dfrac{c}{\sin (C)}\\ a \cdot\dfrac{1}{\sin (A)} \amp = b \cdot \dfrac{1}{\sin (B)} = c \cdot \dfrac{1}{\sin (C)}\\ a \csc (A) \amp = b \csc (B) = c \csc (C) \end{aligned}$

8.4 Chapter Summary and Review
Review Problems

1.

Answer.

False

3.

Answer.

True

5.

Answer.

False

7.

Answer.

False

9.

Answer.

$\dfrac{2-\sqrt{21}}{5\sqrt{2}}$

11.

Answer.

$\displaystyle \dfrac{5\sqrt{33}-3}{32}$
$\displaystyle \dfrac{5\sqrt{33}-3}{\sqrt{5}(3\sqrt{3}+\sqrt{11})}$

13.

Answer.

$1$

15.

Answer.

$\dfrac{\tan (t) + \sqrt{3}}{1-\sqrt{3}\tan (t)}$

17.

Answer.

$\displaystyle \dfrac{4}{5}$
$\displaystyle \dfrac{3}{5}$
$\displaystyle \dfrac{4}{3}$
$\displaystyle \dfrac{24}{25}$
$\displaystyle \dfrac{-7}{25}$
$\displaystyle \dfrac{-24}{7}$

19.

Answer.

$\sin (9x)$

21.

Answer.

$\tan(2\phi - 2)$

23.

Answer.

$\sin (8\theta)$

25.

Answer.

$\displaystyle 1-2\sin^2(\theta) - \sin (\theta) = 1$
$\displaystyle 0,~\pi,~\dfrac{7\pi}{6},~\dfrac{11\pi}{6}$

27.

Answer.

29.

Answer.

$\displaystyle \dfrac{-\pi}{3}$
$\displaystyle \dfrac{2\pi}{3}$

31.

Answer.

$\displaystyle \tan^{-1}\left(\dfrac{52.8}{x}\right)$
$\displaystyle 69.25\degree,~ 27.83\degree$

33.

Answer.

$\theta = \sin^{-1}\left(\dfrac{v_y + gt}{v_0}\right)$

35.

Answer.

$\dfrac{2}{3}$

37.

Answer.

$\sqrt{1-4t^2}$

39.

Answer.

Because $\abs{\sin (\theta)} \le 1, ~\sin^{-1}(t)$ is undefined for $\abs{t} \gt 1\text{.}$ If $x \not= 0\text{,}$ then either $\abs{x} \gt 1$ or $\abs{\dfrac{1}{x}} \gt 1\text{.}$ If $x=0\text{,}$ then $\dfrac{1}{x}$ is undefined.

41.

Answer.

$\displaystyle 2.203$
$\displaystyle -3.236$
$\displaystyle 0.466$

43.

Answer.

$\sin (\theta) = \dfrac{13}{\sqrt{313}}\text{,}$ $~\cos (\theta) = \dfrac{12}{\sqrt{313}}\text{,}$ $~\tan (\theta) = \dfrac{13}{12}\text{,}$ $~\sec (\theta) = \dfrac{\sqrt{313}}{12}\text{,}$ $~\csc (\theta) = \dfrac{\sqrt{313}}{13}\text{,}$ $~\cot (\theta) = \dfrac{12}{13}$

45.

Answer.

$\sin (\theta) = \dfrac{1}{3}\text{,}$ $~\cos (\theta) = \dfrac{-2\sqrt{2}}{3}\text{,}$ $~\tan (\theta) = \dfrac{-1}{2\sqrt{2}}\text{,}$ $~\sec (\theta) = \dfrac{-3}{2\sqrt{2}}\text{,}$ $~\csc (\theta) = 3\text{,}$ $~\cot (\theta) = -2\sqrt{2}$

47.

Answer.

$\sin (\theta) = \dfrac{-9}{\sqrt{106}}\text{,}$ $~\cos (\theta) = \dfrac{-5}{\sqrt{106}}\text{,}$ $~\tan (\theta) = \dfrac{9}{5}\text{,}$ $~\sec (\theta) = \dfrac{-\sqrt{106}}{5}\text{,}$ $~\csc (\theta) = \dfrac{-\sqrt{106}}{9}\text{,}$ $~\cot (\theta) = \dfrac{5}{9}$

49.

Answer.

$\sin (\alpha) = \dfrac{-\sqrt{11}}{6}\text{,}$ $~\cos (\alpha) = \dfrac{-5}{6}\text{,}$ $~\tan (\alpha) = \dfrac{\sqrt{11}}{5}\text{,}$ $~\sec (\alpha) = \dfrac{-6}{5},$$~\csc (\alpha) = \dfrac{-6}{\sqrt{11}}\text{,}$ $~\cot (\alpha) = \dfrac{5}{\sqrt{11}}$

51.

Answer.

$\sin (\theta )= \dfrac{s}{4},$ $~\cos (\theta) = \dfrac{\sqrt{16-s^2}}{4},$ $~\tan (\theta) = \dfrac{s}{\sqrt{16-s^2}},$ $~\sec (\theta) = \dfrac{4}{\sqrt{16-s^2}},$ $~\csc (\theta) = \dfrac{4}{s},$ $~\cot (\theta) = \dfrac{\sqrt{16-s^2}}{s}$

53.

Answer.

$\sin (\theta) = \dfrac{w}{\sqrt{w^2+144}},$ $~\cos (\theta) = \dfrac{-12}{\sqrt{w^2+144}},$ $~\tan (\theta) = \dfrac{-w}{12},$ $~\sec (\theta) = \dfrac{-\sqrt{w^2+144}}{12},$ $~\csc (\theta) = \dfrac{\sqrt{w^2+144}}{w},$ $~\cot (\theta) = \dfrac{-12}{w}$

55.

Answer.

$\sin (\alpha) = \dfrac{k}{2},$ $~\cos (\alpha) = \dfrac{-\sqrt{4-k^2}}{2},$ $~\tan (\alpha) = \dfrac{-k}{\sqrt{4-k^2}},$ $~\sec (\alpha) = \dfrac{-2}{\sqrt{4-k^2}},$ $~\csc (\alpha) = \dfrac{2}{k},$ $~\cot (\alpha) = \dfrac{-\sqrt{4-k^2}}{k}$

57.

Answer.

$\sin (\theta) =0.3\text{,}$ $\cos (\theta) = -0.4\text{,}$ $\tan (\theta) = -0.75\text{,}$ $\sec (\theta) = -2.5\text{,}$ $\csc (\theta) \approx 3.33\text{,}$ $\cot \theta (\approx) -1.33$

59.

Answer.

$-8$

61.

Answer.

$\sqrt{2}$

63.

Answer.

$\theta \approx 2.8,~\theta \approx 0.30$

65.

Answer.

$y = \csc (x)$ or $y = \cot (x)$

67.

Answer.

$y = \sec (x)$

69.

Answer.

$y = \sec (x)$ or $y = \csc (x)$

71.

Answer.

$f(x) = \sin (x) - 1$

73.

Answer.

$G(x) = \tan (x) -1$

75.

Answer.

$\cos^2 (x)$

77.

Answer.

$\cos^2 (B)$

79.

Answer.

$\csc (\theta)$

81.

Answer.

$\sqrt{3} \tan (\theta) \sin (\theta)$

83.

Answer.

$\displaystyle AC = \tan (\alpha),~DC = \tan (\beta),~AD = \tan (\alpha) - \tan (\beta)$
They are right triangles that share $\angle B\text{.}$
$\angle A = \angle F,~ \angle B$ is the complement of $\angle A,$ and $\angle FDC$ is the complement of $\angle F\text{.}$
$\dfrac{CF}{CD} = \tan (\alpha),$ so $CF = \tan (\alpha) \tan (\beta)$
They are right triangles with $\angle A = \angle F\text{.}$
$\angle EBD = \alpha - \beta,$ so $\tan (\alpha - \beta) = \dfrac{\text{opp}}{\text{adj}} = \dfrac{DE}{BE};~~\dfrac{DE}{BE}$ and $\dfrac{AD}{BF}$ are ratios of corresponding sides of similar triangles; $AD = \tan (\alpha) - \tan (\beta)$ by part (a), $BF = BC + CF = 1 + \tan (\alpha) \tan (\beta)$ by part (d).

85.

Answer.

$d=25\csc (112\degree),~\alpha = 45\degree,~a \approx 19.07,~b \approx 10.54$

9 Vectors
9.1 Geometric Form
Homework 9-1

1.

Answer.

$position vector$

3.

Answer.

$velocity vector$

5.

Answer.

$velocity vector$

7.

Answer.

$\bf{A}$ and $\bf{E}$

9.

Answer.

$\bf{H}$ and $\bf{K}$

11.

Answer.

$vecoor on grid$

13.

Answer.

$vector on grid$

15.

Answer.

$triangle$

17.

Answer.

$vectors on grid$

19.

Answer.

$vectors on grid$

$\|{\bf{A}}\| = \sqrt{13},~ \theta = -33.7\degree$

21.

Answer.

$vectors on grid$

$\|{\bf{C}}\| = 1,~ \theta = 90\degree$

23.

Answer.

$vectors on grid$

$\|{\bf{E}}\| = 5,~ \theta = 90\degree$

25.

Answer.

$vector on$

$\|{\bf{G}}\| = 4,~ \theta = 180\degree$

27.

Answer.

$\|{\bf{v}}\| = 13,~ \theta = -67.38\degree$

29.

Answer.

$\|{\bf{v}}\| = \sqrt{85} \approx 9.22,~ \theta = 229.4\degree$

31.

Answer.

$vectors$

$\|{\bf{v} + \bf{w}}\| = 32.9,~ \theta = 109.3\degree$

33.

Answer.

$vectors$

$\|{\bf{v} + \bf{w}}\| = 11.4,~ \theta = 162.4\degree$

35.

Answer.

$vectors$

4.47 mi, $23.4\degree$ east of north

37.

Answer.

$vectors$

129.4 mph, $85.4\degree$ west of north

39.

Answer.

$\displaystyle v_x = 10,~ v_y = 10\sqrt{3},~ w_x = 5\sqrt{2},~ w_y = -5\sqrt{2}$
19.9 mph, $59\degree$ east of north

41.

Answer.

$\displaystyle v_x \approx -1.23,~ v_y \approx 3.38,~ w_x \approx -0.32,~ w_y \approx -2.23$
1.9 km, $54.5\degree$ west of north

43.

Answer.

$vectors on grid$

45.

Answer.

$vectors on grid$

47.

Answer.

$vectors on grid$

49.

Answer.

$vectors on grid$

51.

Answer.

$u_x = 2\text{,}$ $~ u_y = 1\text{,}$ $~ v_x = 1\text{,}$$~ v_y = -3\text{,}$ $~ A_x = 1\text{,}$ $~ A_y = 4\text{;}$ $~ A_x = u_x - v_x\text{,}$ $~ A_y = u_y - v_y$

9.2 Coordinate Form
Homework 9-2

1.

Answer.

${\bf{u}} = 3{\bf{i}}+2{\bf{j}}$

$\displaystyle \sqrt{13}$
$\displaystyle 6{\bf{i}}+4{\bf{j}}$
$\displaystyle 2\sqrt{13}$

3.

Answer.

${\bf{w}} = 6{\bf{i}}-3{\bf{j}}$

$\displaystyle 3\sqrt{5}$
$\displaystyle -6{\bf{i}}+3{\bf{j}}$
$\displaystyle 3\sqrt{5}$

5.

Answer.

${\bf{u}}+{\bf{v}} = -2{\bf{i}}+5{\bf{j}}$ and $\|{\bf{u}}+{\bf{v}}\| = \sqrt{29}$
$\displaystyle \|{\bf{u}}\|+\|{\bf{v}}\| \ge \|{\bf{u}}+{\bf{v}}\|$

7.

Answer.

$vector$

$-5{\bf{i}}+8{\bf{j}}$
$\displaystyle \|{\bf{v}}\| = \sqrt{89},~~\theta = 122\degree$

9.

Answer.

$vector$

$-2{\bf{i}}-{\bf{j}}$
$\displaystyle \|{\bf{v}}\| = \sqrt{5},~~\theta = 206.6\degree$

11.

Answer.

$\displaystyle 18{\bf{i}}+12{\bf{j}}$
$\displaystyle \|{\bf{v}}\| = 6\sqrt{13},~~\theta = 33.7\degree$

13.

Answer.

$\|{\bf{v}}\| = 6\sqrt{2},~~\theta = 135\degree$

15.

Answer.

$\|{\bf{w}}\| = 14,~~\theta = -30\degree$

17.

Answer.

$\|{\bf{q}}\| = 4\sqrt{745},~~\theta = 61.56\degree$

19.

Answer.

${\bf{v}} = 3\sqrt{2}{\bf{i}}-3\sqrt{2}{\bf{j}}$

21.

Answer.

${\bf{v}} \approx 6.629{\bf{i}}+4.995{\bf{j}}$

23.

Answer.

${\bf{i}}-2{\bf{j}}$

$vectors$

25.

Answer.

$-4{\bf{i}}+4{\bf{j}}$

$vectors$

27.

Answer.

$12{\bf{i}}+3{\bf{j}}$

29.

Answer.

$2.8{\bf{i}}+1.9{\bf{j}}$

31.

Answer.

$-3{\bf{i}}+7{\bf{j}}$

33.

Answer.

$-8{\bf{i}}-20{\bf{j}}$

35.

Answer.

$14{\bf{i}}-9{\bf{j}}$

37.

Answer.

$-9{\bf{i}}+23{\bf{j}}$

39.

Answer.

$\dfrac{-12}{13}{\bf{i}}+\dfrac{5}{13}{\bf{j}}$

41.

Answer.

$\dfrac{1}{\sqrt{2}}{\bf{i}}-\dfrac{1}{\sqrt{2}}{\bf{j}}$

43.

Answer.

$24{\bf{i}}+45{\bf{j}}$

45.

Answer.

$\dfrac{-12}{\sqrt{10}}{\bf{i}}+\dfrac{4}{\sqrt{10}}{\bf{j}}$

47.

Answer.

$vectors$
$\displaystyle {\bf{u}}=2.393{\bf{i}}+1.016{\bf{j}},~~{\bf{v}}=-4.242{\bf{i}}-3.956{\bf{j}}$
$\displaystyle -1.849{\bf{i}}-2.940{\bf{j}}$

49.

Answer.

$vectors$
$\displaystyle {\bf{u}}=-11.97{\bf{i}}+32.889{\bf{j}},~~{\bf{v}}=-57.955{\bf{i}}+15.529{\bf{j}}$
$\displaystyle 45.98{\bf{i}}+17.36{\bf{j}}$

51.

Answer.

$vectors$
1700 m, $28.1\degree$ east of south

53.

Answer.

$vectors$
21.98 km, $2.27\degree$ north of west

55.

Answer.

$vectors$
83 mi, $62\degree$ east of north

57.

Answer.

$\displaystyle -4{\bf{i}}-5{\bf{j}}$
$\displaystyle 4{\bf{i}}+5{\bf{j}}$

59.

Answer.

$\displaystyle {\bf{i}}-3{\bf{j}}$
$\displaystyle -{\bf{i}}+3{\bf{j}}$

61.

Answer.

$\displaystyle \|{\bf{v}}\| = 10,~ 2\|{\bf{v}}\| = 20 = 2 \cdot 10$
$\displaystyle \|k{\bf{v}}\| = \sqrt{(ka)^2 +(kb)^2} = k\sqrt{a^2 + b^2}$

9.3 The Dot Product
Homework 9-3

1.

Answer.

$\dfrac{33}{\sqrt{13}}$

3.

Answer.

$\dfrac{-1}{\sqrt{2}}$

5.

Answer.

$-2\sqrt{5}$

7.

Answer.

$\displaystyle {\bf{w}} = \left(\dfrac{56}{13}{\bf{i}}+\dfrac{84}{13}{\bf{j}}\right) + \left(\dfrac{48}{13}{\bf{i}}-\dfrac{32}{13}{\bf{j}}\right)$
$vectors$

9.

Answer.

$\displaystyle {\bf{w}} = (4{\bf{i}}-4{\bf{j}}) + (2{\bf{i}}+2{\bf{j}})$
$vectors$

11.

Answer.

$22$

13.

Answer.

$0$

15.

Answer.

$12$

17.

Answer.

$-318.2$

19.

Answer.

not orthogonal

21.

Answer.

orthogonal

23.

Answer.

$4.4\degree$

25.

Answer.

$97.1\degree$

27.

Answer.

$8$

29.

Answer.

$-10$

31.

Answer.

$-21$

33.

Answer.

$42{\bf{i}}-28{\bf{j}}$

35.

Answer.

$4$

37.

Answer.

38.57 lbs

39.

Answer.

1289 lbs

41.

Answer.

$\displaystyle \dfrac{1}{\sqrt{2}}{\bf{i}}+\dfrac{1}{\sqrt{2}}{\bf{j}}~~\text{and}~~\dfrac{-1}{\sqrt{2}}{\bf{i}}+\dfrac{1}{\sqrt{2}}{\bf{j}}$
$\displaystyle {\bf{u}} \cdot {\bf{v}} = 0$
$\dfrac{11}{\sqrt{2}}$ and $\dfrac{5}{\sqrt{2}}$
$orthogonal vectors$

43.

Answer.

${\bf{v}} \cdot {\bf{v}} = c^2 + d^2$

45.

Answer.

$k{\bf{u}} \cdot {\bf{v}} = kac+kbd = k(ac+bd) = (akc + bkd)$

47.

Answer.

$\begin{aligned}[t] ({\bf{u}}-{\bf{v}}) \cdot ({\bf{u}}+{\bf{v}}) \amp= (a-c)(a+c)+(b-d)(b+d)\\ \amp= (a^2+b^2)-(c^2+d^2)\end{aligned}$

49.

Answer.

$\dfrac{a \cdot 1 + b \cdot 0}{1} = a$ and $\dfrac{a \cdot 0 + b \cdot 1}{1} = b$

51.

Answer.

Both ${\bf{i}} \cdot {\bf{i}}=1$ and ${\bf{j}} \cdot {\bf{j}}=1$ because $1 \cdot 1 \cos 0 = 1\text{;}$ ${\bf{i}} \cdot {\bf{j}} = 1 \cdot 1 \cos 90\degree =0$
$\displaystyle (a{\bf{i}}+b{\bf{j}}) \cdot (c{\bf{i}}+d{\bf{j}}) = ac(1) + ad(0) + bc(0) + bd(1) = ac+bd$

53.

Answer.

$\displaystyle \|{\bf{u}}-{\bf{v}}\|^2 = {\bf{u}} \cdot {\bf{u}} - 2{\bf{u}} \cdot {\bf{v}} +{\bf{v}} \cdot {\bf{v}}= \|{\bf{u}}\|^2+\|{\bf{v}}\|^2 - 2\|{\bf{u}}\|\|{\bf{v}}\|\cos \theta$
Let $a = \|{\bf{u}}\|,~ b = \|{\bf{v}}\|,~c = \|{\bf{u}}-{\bf{v}}\|\text{,}$ and $C = \theta$

9.4 Chapter Summary and Review
Review Problems

1.

Answer.

$vector$

$v_N=8.45$ mph, $v_E=-18.13$ mph

3.

Answer.

$vector$

$v_N=-1127.63$ lbs, $v_E=-410.42$ lbs

5.

Answer.

$\|{\bf{A}}\|=10.9,~\theta = 236.3\degree$

7.

Answer.

${\bf{i}}-\sqrt{3}{\bf{j}}$

9.

Answer.

$vector$

$15{\bf{i}}+3{\bf{j}}$
$\displaystyle \|{\bf{v}}\|=15.3,~\theta = 11.3\degree$

11.

Answer.

$vector$

$2{\bf{i}}-6{\bf{j}}$
$\displaystyle \|{\bf{v}}\|=6.3~\text{mi},~\theta = 288.4\degree$

13.

Answer.

$vectors$
$\displaystyle 7.64~\text{km},~\theta = 30.31\degree$

15.

Answer.

$vectors$
$\displaystyle 8.46~\text{mi},~\theta = 155.6\degree$

17.

Answer.

${\bf{F_1}}=-200{\bf{i}},~{\bf{F_2}}=-60\sqrt{2}{\bf{i}}-60\sqrt{2}{\bf{j}},~{\bf{F_3}}=50\sqrt{3}{\bf{i}}+50{\bf{j}},$ ${\bf{F_4}}=-125{\bf{i}}+125\sqrt{3}{\bf{j}}$
$\displaystyle -73.25{\bf{i}}+181.65{\bf{j}}$

19.

Answer.

$13{\bf{i}}+5{\bf{j}}$

21.

Answer.

$-7{\bf{i}}-14{\bf{j}}$

23.

Answer.

$\dfrac{2}{\sqrt{13}}{\bf{i}}+\dfrac{3}{\sqrt{13}}{\bf{j}}$

25.

Answer.

$\dfrac{-6}{\sqrt{29}}{\bf{i}}-\dfrac{15}{\sqrt{29}}{\bf{j}}$

27.

Answer.

$-3.45$

29.

Answer.

$-8.08$

31.

Answer.

$106.26\degree$

10 Polar Coordinates and Complex Numbers
10.1 Polar Coordinates
Homework 10-1

1.

Answer.

$polar plot$

3.

Answer.

$polar plot$

5.

Answer.

$polar plot$

7.

Answer.

$polar plot$

9.

Answer.

$\left(5, \dfrac{3\pi}{4}\right)$

11.

Answer.

$(1, \pi)$

13.

Answer.

$\left(3, \dfrac{4\pi}{3}\right)$

15.

Answer.

$\left(2, \dfrac{\pi}{12}\right)$

17.

Answer.

$(-3, 3\sqrt{3})$

19.

Answer.

$\left(\dfrac{3}{\sqrt{2}}, \dfrac{-3}{\sqrt{2}}\right)$

21.

Answer.

$(-2.15, -1.06)$

23.

Answer.

$(-0.14, -1.99)$

25.

Answer.

$\left(7\sqrt{2}, \dfrac{\pi}{4}\right)$

27.

Answer.

$\left(2\sqrt{2}, \dfrac{11\pi}{6}\right)$

29.

Answer.

$\left(\sqrt{13}, \pi+\tan^{-1}\dfrac{2}{3}\right)$

31.

Answer.

$(2, \pi)$

33.

Answer.

$\displaystyle \left(-2, \dfrac{11\pi}{6}\right)$
$\displaystyle \left(2, \dfrac{-7\pi}{6}\right)$

35.

Answer.

$\displaystyle (-3,0)$
$\displaystyle (3, -\pi)$

37.

Answer.

$\displaystyle (-2.3, 2.06)$
$\displaystyle (2.3, -1.08)$

39.

Answer.

$polar plot$

41.

Answer.

$polar grid$

43.

Answer.

$polar grid$

45.

Answer.

$r \ge 0,~ \dfrac{\pi}{6} \le \theta \le \dfrac{\pi}{3}$

47.

Answer.

$r \ge 1,~ \dfrac{\pi}{2} \le \theta \le \pi$

49.

Answer.

$-1 \le r \le 1,~ \dfrac{3\pi}{4} \le \theta \le \pi$

51.

Answer.

$x^2+y^2=2$

53.

Answer.

$x^2+y^2=4x$

55.

Answer.

$y=1$

57.

Answer.

$y=2x$

59.

Answer.

$x^2+y^2=3x$

61.

Answer.

$x^2=4-4y$

63.

Answer.

$2x+y=1$

65.

Answer.

$r=2\sec (\theta)$

67.

Answer.

$2r^2=\sec (\theta) \csc (\theta)$

69.

Answer.

$r=4\cot (\theta) \csc (\theta)$

71.

Answer.

$r=4$

73.

Answer.

\begin{align*} d \amp =\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ \amp = \sqrt{(r_2\cos(\theta_2)-r_1\cos(\theta_1))^2 +(r_2\sin(\theta_2)-r_1\sin(\theta_1))^2}\\ \amp = \sqrt{r_2^2\cos^2(\theta_2) - 2r_2r_1\cos(\theta_2)\cos(\theta_1)+r_1^2\cos^2(\theta_1)+r_2^2\sin^2(\theta_2) - 2r_2r_1\sin(\theta_2)\sin(\theta_1)+r_1^2\sin^2(\theta_1)}\\ \amp = \sqrt{r_2^2+r_1^2 - 2r_2r_1(\cos(\theta_2)\cos(\theta_1)-\sin(\theta_2)\sin(\theta_1))}\\ \amp = \sqrt{r_1^2 + r_2^2 - 2r_1r_2\cos (\theta_2 - \theta_1)} \end{align*}

10.2 Polar Graphs
Homework 10-2

1.

Answer.

$circles$

$k$ is the radius
$\displaystyle x^2+y^2=1,~ x^2+y^2=4,~ x^2+y^2=9$

3.

Answer.

$lines on polar grid$

$\tan k$ is the slope
$\displaystyle y=\dfrac{x}{\sqrt{3}},~ y=\sqrt{3}x,~ y=-\sqrt{3}x,~ y=\dfrac{x}{\sqrt{3}}$

5.

Answer.

$\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$
$r=2$	$2$	$2$	$2$	$2$	$2$	$2$	$2$	$2$

$\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$
$r=-2$	$-2$	$-2$	$-2$	$-2$	$-2$	$-2$	$-2$	$-2$

The graph of $r=2$ begins at the right-most point (and proceeds counter-clockwise); the graph of $r=-2$ begins at the left-most point.

$polar points on circle$

7.

Answer.

$circle on polar grid$
$\theta$ $\pi$ $\dfrac{5\pi}{4}$ $\dfrac{3\pi}{2}$ $\dfrac{7\pi}{4}$ $2\pi$

$r$ $-4$ $-2\sqrt{2}$ $0$ $2\sqrt{2}$ $4$

The graph is traced again.
center: $(2,0)\text{,}$ radius: $2$
$\displaystyle (x-2)^2+y^2=4$

9.

Answer.

$circcles on polar grid$
For $a \gt 0\text{,}$ $a$ is the radius of a circle centerd on the positive $y$-axis; for $a \lt 0\text{,}$ $\abs{a}$ is the radius of a circle centerd on the negative $y$-axis.

11.

Answer.

$cardioid$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $1$ $2$ $1$ $0$ $1$
$cardioid$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $-1$ $0$ $-1$ $-2$ $-1$
$cardioid$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $1$ $0$ $1$ $2$ $1$
$cardioid$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $-1$ $-2$ $-1$ $0$ $-1$

13.

Answer.

$limacon$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $3$ $2$ $1$ $2$ $3$
$limacon$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $1$ $2$ $3$ $2$ $1$
$limacon$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $3$ $1$ $-1$ $1$ $3$
$limacon$

$\theta$ $0$ $\dfrac{\pi}{2}$ $\pi$ $\dfrac{3\pi}{2}$ $2\pi$

$r$ $-1$ $1$ $3$ $1$ $-1$

15.

Answer.

$4-petal rose$

$3-petal rose$

$8-petal rose$

$5 petal rose$

There are $n$ petals if $n$ is odd, and $2n$ petals if $n$ is even.
$n=2:~ \dfrac{\pi}{4},$ $~ \dfrac{3\pi}{4},~$$\dfrac{5\pi}{4},~$$\dfrac{7\pi}{4};~$ $n=3:~\dfrac{\pi}{6},~$$\dfrac{5\pi}{6},~$$\dfrac{3\pi}{2};$ $n=4:~ \dfrac{\pi}{8},~$$\dfrac{3\pi}{8},~$$\dfrac{5\pi}{8},~$$\dfrac{7\pi}{8},~$$\dfrac{9\pi}{8},~$$\dfrac{11\pi}{8},~$$\dfrac{13\pi}{8},~$$\dfrac{15\pi}{8};$ $n=5:~~\dfrac{\pi}{10},~$$\dfrac{\pi}{2},~$$\dfrac{9\pi}{10},~$$\dfrac{13\pi}{10},~$$\dfrac{17\pi}{10}$
$3-petal rose$

$3-petal rose$

$3-petal rose$

$a$ is the length of the petal.

17.

Answer.

$\displaystyle r=\pm 3\sqrt{\cos 2\theta}$
$lemniscate$
$a$ is the length of the loop.

19.

Answer.

$Archimedean spiral$

21.

Answer.

$\theta$	$0$	$\dfrac{\pi}{12}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{5\pi}{12}$	$\dfrac{\pi}{2}$	$\dfrac{7\pi}{12}$	$\dfrac{2\pi}{3}$
$3\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$	$0$	$\dfrac{\sqrt{2}}{2}$	$1$	$\dfrac{\sqrt{2}}{2}$	$0$	$\dfrac{-\sqrt{2}}{2}$	$-1$	$\dfrac{-\sqrt{2}}{2}$	$0$

$sinusoidal curve$

$\theta$	$0$	$\dfrac{\pi}{12}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{5\pi}{12}$	$\dfrac{\pi}{2}$	$\dfrac{7\pi}{12}$	$\dfrac{2\pi}{3}$
$3\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$	$0$	$\dfrac{\sqrt{2}}{2}$	$1$	$\dfrac{\sqrt{2}}{2}$	$0$	$\dfrac{-\sqrt{2}}{2}$	$-1$	$\dfrac{-\sqrt{2}}{2}$	$0$

$three-petal rose$

23.

Answer.

$\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$	$4$	$2+\sqrt{2}$	$2$	$2-\sqrt{2}$	$0$	$2-\sqrt{2}$	$2$	$2+\sqrt{2}$	$4$

$sinusoidal graph$

$\theta$	$0$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$	$4$	$2+\sqrt{2}$	$2$	$2-\sqrt{2}$	$0$	$2-\sqrt{2}$	$2$	$2+\sqrt{2}$	$4$

$cardioid$

25.

Answer.

circle

$circle on polar grid$

27.

Answer.

line

$line on polar grid$

29.

Answer.

circle

$circle$

31.

Answer.

cardioid

$cardioid$

33.

Answer.

limaçon

$limacon$

35.

Answer.

rose

$four-petal rose$

37.

Answer.

rose

$rose$

39.

Answer.

limaçon

$limacon$

41.

Answer.

lemniscate

$lemniscate$

43.

Answer.

circle

$circle$

45.

Answer.

arcs of a circle

$arcs of circle$

47.

Answer.

semicircle

$semicircle$

49.

Answer.

rose

$eight-petal rose$

51.

Answer.

cardioid

$cardioid$

53.

Answer.

parabola

$parabola$

55.

Answer.

ellipse

$ellipse$

57.

Answer.

hyperbola

$hyperbola$

59.

Answer.

$r=2+2\cos (\theta)$

61.

Answer.

$r=3\sin (5\theta)$

63.

Answer.

$r=5\sin (\theta)$

65.

Answer.

$r=1+2\cos (\theta)$

67.

Answer.

$(0,0)\text{,}$$~ \left(\dfrac{1}{2},\dfrac{\pi}{3}\right)\text{,}$$~ \left(\dfrac{1}{2},\dfrac{5\pi}{3}\right) $

69.

Answer.

$(0,0)\text{,}$ $~ \left(\dfrac{3}{\sqrt{2}}, \dfrac{\pi}{4}\right)\text{,}$ $~ \left(\dfrac{-3}{\sqrt{2}}, \dfrac{5\pi}{4}\right)$

71.

Answer.

$\left(1, \dfrac{\pi}{2}\right)\text{,}$ $~\left(1, \dfrac{3\pi}{2}\right)$

73.

Answer.

$\left(\dfrac{4+\sqrt{2}}{2},\dfrac{3\pi}{4}\right)\text{,}$ $~\left(\dfrac{4-\sqrt{2}}{2},\dfrac{7\pi}{4}\right)$

75.

Answer.

$polar plot$

77.

Answer.

$conchoid$

79.

Answer.

$strophoid$

81.

Answer.

$polar plot$

83.

Answer.

The curve has $n$ large loops and $n$ small loops.

10.3 Complex Numbers
Homework 10-3

1.

Answer.

$\displaystyle 5i-4$
$\displaystyle -4+i$
$\displaystyle \dfrac{-5}{6}-\dfrac{\sqrt{2}}{6}i$

3.

Answer.

$-3\pm 2i$

5.

Answer.

$\dfrac{1}{6} \pm \dfrac{\sqrt{11}}{6}i$

7.

Answer.

$13+4i$

9.

Answer.

$-0.8+3.8i$

11.

Answer.

$20-10i$

13.

Answer.

$-14+34i$

15.

Answer.

$46+14i\sqrt{3}$

17.

Answer.

$52$

19.

Answer.

$-2-2i$

21.

Answer.

$-1+4i$

23.

Answer.

$\dfrac{35}{3}+\dfrac{20}{3}i$

25.

Answer.

$\dfrac{-25}{29}+\dfrac{10}{29}i$

27.

Answer.

$\dfrac{3}{4}-\dfrac{\sqrt{3}}{4}i$

29.

Answer.

$\dfrac{-2}{3}+\dfrac{\sqrt{5}}{3}i$

31.

Answer.

$i$

33.

Answer.

$\displaystyle -1$
$\displaystyle 1$
$\displaystyle -i$
$\displaystyle -1$

35.

Answer.

$\displaystyle 0$
$\displaystyle 0$

37.

Answer.

$\displaystyle 0$
$\displaystyle 0$

39.

Answer.

$\displaystyle 0$
$\displaystyle 0$

41.

Answer.

$4z^2+49$

43.

Answer.

$x^2+6x+10$

45.

Answer.

$v^2-8v+17$

47.

Answer.

$complex conjugates$

49.

Answer.

$complex conjugates$

51.

Answer.

$disk$

53.

Answer.

$inequality$

55.

Answer.

$complex numbers as vectors$

57.

Answer.

$complex numbers as vectors$

59.

Answer.

$(a+bi)(c+di) = ac+adi+bci+bdi^2=(ac-bd)+(ad+bc)i$

61.

Answer.

\begin{align*} z_1+z_2 \amp =(a+bi)+(c+di)=(a+c)+(b+d)i\\ \amp =(c+a)+(d+b)i=(c+di)+(a+bi)=z_2+z_1 \end{align*}

\begin{align*} z_1z_2 \amp =(a+bi)(c+di) = (ac-bd)+(ad+bc)i\\ \amp =(ca-db)+(da+cb)i=z_2z_1 \end{align*}

63.

Answer.

$z+\bar{z}=(a+bi)+(a-bi)=2a;~~~$ $z-\bar{z}=(a+bi)-(a-bi)=-2bi$
$\displaystyle z\bar{z}=(a+bi)(a-bi)=a^2+b^2=\abs{z}^2$

65.

Answer.

No. Let $t=i$ and $z=-i\text{.}$ Then $w=t+z=i-i=0,$ so $\abs{w}=0,$ but $\abs{t}+\abs{z}=\abs{i}+\abs{-i}=1+1=2.$

67.

Answer.

$\displaystyle 2-\sqrt{5}$
$\displaystyle x^2-4x-1=0$

69.

Answer.

$\displaystyle 4+3i$
$\displaystyle x^2-8x+25=0$

71.

Answer.

$x^4-6x^3+23x^2-50x+50=0$

73.

Answer.

$x^4-7x^3+20x^2-19x+13=0$

10.4 Polar Form for Complex Numbers
Homework 10-4

1.

Answer.

$1\text{,}$ $~i\text{,}$ $~-1\text{,}$$~-i\text{,}$ $~1$

$powers of i$

3.

Answer.

$1+2i\text{,}$ $-2+i$

$complex numbers$

5.

Answer.

$-3+3i\sqrt{3}$

7.

Answer.

$-1+i$

9.

Answer.

$2.34-4.21i$

11.

Answer.

$-5.07+10.88i$

13.

Answer.

$3\left(\cos \left(\dfrac{\pi}{2}\right) + i\sin \left(\dfrac{\pi}{2}\right)\right)\text{,}$ $3\left(\cos \left(\dfrac{3\pi}{2}\right) + i\sin \left(\dfrac{3\pi}{2}\right)\right)$

15.

Answer.

$2\sqrt{3}\left(\cos \left(\dfrac{7\pi}{6}\right) + i\sin \left(\dfrac{7\pi}{6}\right)\right)\text{,}$ $2\sqrt{3}\left(\cos \left(\dfrac{11\pi}{6}\right) + i\sin \left(\dfrac{11\pi}{6}\right)\right)$

17.

Answer.

$4.47(\cos (2.68) + i\sin (2.68)),~$ $4.47(\cos (5.82) + i\sin (5.82))$

19.

Answer.

$8.60(\cos (5.78) + i\sin (5.78)),~$ $8.60(\cos (0.51) + i\sin (0.51))$

21.

Answer.

$5(\cos (0.93) + i\sin (0.93)),~$ $5(\cos (5.36) + i\sin (5.36)),~$ $5(\cos (2.21) + i\sin (2.21)),~$ $5(\cos (4.07) + i\sin (4.07))$

23.

Answer.

If $z=r(\cos (\theta)+ i\sin (\theta)),$ then $\bar{z}=r(\cos (2\pi -\theta) + i\sin (2\pi -\theta)$

25.

Answer.

$z_1z_2 = 2\left(\cos \left(\dfrac{\pi}{6}\right) + i\sin \left(\dfrac{\pi}{6}\right)\right) = \sqrt{3} + i\text{;}$$~~\dfrac{z_1}{z_2}=8\left(\cos \left(\dfrac{\pi}{2}\right) + i\sin \left(\dfrac{\pi}{2}\right)\right) = 8i$

27.

Answer.

$z_1z_2 = 6\left(\cos \left(\dfrac{9\pi}{10}\right) + i\sin \left(\dfrac{9\pi}{10}\right)\right)\text{;}$ $~~\dfrac{z_1}{z_2}=\dfrac{3}{2}\left(\cos \left(\dfrac{3\pi}{10}\right) + i\sin \left(\dfrac{3\pi}{10}\right)\right)$

29.

Answer.

$z_1z_2 = 8\text{;}$ $~\dfrac{z_1}{z_2}=\dfrac{1}{2}$

31.

Answer.

$z_1z_2 = 4\sqrt{2}(\cos \dfrac{7\pi}{12} + i\sin \dfrac{7\pi}{12})\text{;}$ $~~\dfrac{z_1}{z_2}=2\sqrt{2}(\cos \dfrac{13\pi}{12} + i\sin \dfrac{13\pi}{12})$

33.

Answer.

$-128-128i$

35.

Answer.

$-128-128\sqrt{3}i$

37.

Answer.

$512+512\sqrt{3}i$

39.

Answer.

$\dfrac{1}{4}+\dfrac{1}{4}i$

41.

Answer.

$\dfrac{-\sqrt{2}}{8}-\dfrac{\sqrt{6}}{8}i$

43.

Answer.

$3(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4})\text{,}$ $~3(\cos \dfrac{3\pi}{4} + i\sin \dfrac{3\pi}{4})$
$\dfrac{3}{\sqrt{2}}+\dfrac{3}{\sqrt{2}}i\text{,}$ $~\dfrac{-3}{\sqrt{2}}-\dfrac{3}{\sqrt{2}}i$

$square roots$

45.

Answer.

$2,~2\left(\cos \dfrac{2\pi}{5} + i\sin \dfrac{2\pi}{5}\right)\text{,}$ $~2\left(\cos \dfrac{4\pi}{5} + i\sin \dfrac{4\pi}{5}\right)$ , $~2\left(\cos \dfrac{6\pi}{5} + i\sin \dfrac{6\pi}{5}\right)\text{,}$ $2\left(\cos \dfrac{8\pi}{5} + i\sin \dfrac{8\pi}{5}\right)$
$2,~0.618+1.9i\text{,}$ $-1.618+1.176i\text{,}$ $-1.618-1.176i\text{,}$ $0.618-1.902i$

$fifth roots of complex number$

47.

Answer.

$4\left(\cos \dfrac{\pi}{18} + i\sin \dfrac{\pi}{18}\right)\text{,}$ $~4\left(\cos \dfrac{13\pi}{18} + i\sin \dfrac{13\pi}{18}\right)\text{,}$ $~4\left(\cos \dfrac{25\pi}{18} + i\sin \dfrac{25\pi}{18}\right)$
$1.97+0.347i\text{,}$ $~-1.286+1.532i\text{,}$ $~-0.684-1.879i$

$cube roots of complex number$

49.

Answer.

$\abs{z} = \abs{\cos (\theta) + i\sin (\theta)} = \sqrt{\cos^2(\theta) + \sin^2(\theta)} = 1$

51.

Answer.

$\displaystyle 1,~(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}),~(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3})$
$\displaystyle 1,~i,~-1,~-i$
$1,~(\cos \dfrac{2\pi}{5} + i\sin \dfrac{2\pi}{5}),~(\cos \dfrac{4\pi}{5} + i\sin \dfrac{4\pi}{5}),$ $(\cos \dfrac{6\pi}{5} + i\sin \dfrac{6\pi}{5}),~(\cos \dfrac{8\pi}{5} + i\sin \dfrac{8\pi}{5})$
$1,~(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}),~(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3}),~-1,$ $(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3}),~(\cos \dfrac{5\pi}{3} + i\sin \dfrac{5\pi}{3})$

53.

Answer.

$(\omega_k)^n = 1^n \left(\cos \left(n \cdot \dfrac{2\pi k}{n}\right) + i\sin \left(n \cdot \dfrac{2\pi k}{n}\right)\right) = 1(\cos 2\pi k + i\sin 2\pi k) = 1$

55.

Answer.

$8^{1/4}\left(\cos \left(\dfrac{3\pi}{8}\right) + i\sin \left(\dfrac{3\pi}{8}\right)\right)\text{,}$ $~8^{1/4}\left(\cos \left(\dfrac{5\pi}{8}\right) + i\sin \left(\dfrac{5\pi}{8}\right)\right)\text{,}$ $~8^{1/4}\left(\cos \left(\dfrac{11\pi}{8}\right) + i\sin \left(\dfrac{11\pi}{8}\right)\right)\text{,}$ $~8^{1/4}\left(\cos \left(\dfrac{13\pi}{8}\right) + i\sin \left(\dfrac{13\pi}{8}\right)\right)$

57.

Answer.

$\sqrt{2}\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{\pi}{3}\right) + i\sin \left(\dfrac{\pi}{3}\right)\right)\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{2\pi}{3}\right) + i\sin \left(\dfrac{2\pi}{3}\right)\right)\text{,}$ $~-\sqrt{2}\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{4\pi}{3}\right) + i\sin \left(\dfrac{4\pi}{3}\right)\right)\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{5\pi}{3}\right) + i\sin \left(\dfrac{5\pi}{3}\right)\right)$

59.

Answer.

$\sqrt{2}\left(\cos \left(\dfrac{\pi}{3}\right) + i\sin \left(\dfrac{\pi}{3}\right)\right)\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{2\pi}{3}\right) + i\sin \left(\dfrac{2\pi}{3}\right)\right)\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{4\pi}{3}\right) + i\sin \left(\dfrac{4\pi}{3}\right)\right)\text{,}$ $~\sqrt{2}\left(\cos \left(\dfrac{5\pi}{3}\right) + i\sin \left(\dfrac{5\pi}{3}\right)\right)$

61.

Answer.

$\displaystyle \cos^2 (\theta) - \sin^2 (\theta) +(2\sin (\theta) \cos (\theta))i$
$\displaystyle \cos (2\theta) + i\sin (2\theta)$
$\displaystyle \sin (2\theta) = 2\sin (\theta) \cos (\theta);~~\cos (2\theta) = \cos^2 (\theta) - \sin^2 (\theta)$

63.

Answer.

$\displaystyle \dfrac{b}{a}$
$\displaystyle \dfrac{-a}{b}$
$-1\text{,}$ $~\dfrac{\pi}{2}$

65.

Answer.

$\displaystyle z_1z_2 = (ac-bd) + (ad+bc)i$
$\displaystyle a=r\cos(\alpha),~b=r\sin(\alpha),~c=R\cos(\beta),~d=R\sin(\beta)$
$(ac-bd) + (ad+bc)i = (rR\cos(\alpha)\cos(\beta) - rR\sin(\alpha)\sin(\beta))$ $+ (rR\cos(\alpha)\sin(\beta)+rR\sin(\alpha)\cos(\beta))i$
$\displaystyle rR(\cos (\alpha+\beta) +i\sin (\alpha+\beta))$

10.5 Chapter Summary and Review
Review Problems

1.

Answer.

$polar plot$

3.

Answer.

$polar plot$

5.

Answer.

$\left(\dfrac{-\sqrt{2}}{2},\dfrac{-\sqrt{2}}{2}\right)$

7.

Answer.

$(0.241, -3.391)$

9.

Answer.

$(3\sqrt{2}, \dfrac{3\pi}{4})$

11.

Answer.

$(\sqrt{29}, \tan^{-1}(\dfrac{-2}{5})+2\pi)$

13.

Answer.

$region on polar grid$

15.

Answer.

$region on polar grid$

17.

Answer.

$x^2+y^2=1$

19.

Answer.

$x^2+y^2=(2x+6)^2$

21.

Answer.

$r\cos(\theta)+r\sin(\theta)=2$

23.

Answer.

$\tan(\theta)=r$

25.

Answer.

Circle of radius 3 centered at the origin

27.

Answer.

Circle of radius 3 centered at $(3,0)$

29.

Answer.

$r=4$

31.

Answer.

$r=4\cos(\theta)$

33.

Answer.

$\left(4, \dfrac{\pi}{6}\right)\text{,}$ $~\left(4, \dfrac{5\pi}{6}\right)$

35.

Answer.

$\left(2\sqrt{2}, \dfrac{3\pi}{4}\right)$ and the pole

37.

Answer.

$4-3i$

39.

Answer.

$-2+4i$

41.

Answer.

$\displaystyle 1$
$\displaystyle 1$

43.

Answer.

$\displaystyle -44$
$\displaystyle -44$

45.

Answer.

$(2\pm i)^2-4(2\pm i)+5=(4\pm 4i-1)-(8 \pm 4i)+5=0$

47.

Answer.

$z^2+4z+5$

49.

Answer.

$s^2-10s+41$

51.

Answer.

$complex numbers$

53.

Answer.

$\displaystyle -1-7i$
$\displaystyle x^2+2x+50=0$

55.

Answer.

$\displaystyle 3+\sqrt{2}i$
$\displaystyle x^2-6x+11=0$

57.

Answer.

$5\sqrt{3}-5i$

59.

Answer.

$5+5i$

61.

Answer.

$3\sqrt{2}\left(\cos\left(\dfrac{7\pi}{4}\right)+ i\sin\left(\dfrac{7\pi}{4}\right)\right)$

63.

Answer.

$5(\cos (\pi) +i\sin (\pi))$

65.

Answer.

$2\left(\cos\left(\dfrac{4\pi}{3}\right)+i\sin\left(\dfrac{4\pi}{3}\right)\right)$

67.

Answer.

$\begin{aligned}[t] z_1z_2 \amp=16(\cos (\pi) +i\sin (\pi)) \\ \amp=-16,~\dfrac{z_1}{z_2} \\ \amp=4\left(\cos\left(\dfrac{-2\pi}{3}\right)+i\sin\left(\dfrac{-2\pi}{3}\right)\right) \\ \amp=-2-2\sqrt{3}i \end{aligned}$

69.

Answer.

$\begin{aligned}[t] z_1z_2\amp=\dfrac{5}{2}\left(\cos\left(\dfrac{-\pi}{3}\right)+i\sin\left(\dfrac{-\pi}{3}\right)\right) \\ \amp=\dfrac{5}{4}-\dfrac{5\sqrt{3}}{2}i\end{aligned},$ $\begin{aligned}[t] \dfrac{z_1}{z_2} \amp=10\left(\cos\left(\dfrac{-5\pi}{6}\right)+i\sin\left(\dfrac{-5\pi}{6}\right)\right) \\ \amp=-5\sqrt{3}-5i \end{aligned}$

71.

Answer.

$1$

73.

Answer.

$\dfrac{-1}{100}$

75.

Answer.

$complex square roots$
$-2\sqrt{2}+2\sqrt{2}i\text{,}$ $~2\sqrt{2}-2\sqrt{2}i$

77.

Answer.

$complex cube roots$
$3i\text{,}$ $~\dfrac{-3\sqrt{3}}{2}-\dfrac{3}{2}i\text{,}$ $~\dfrac{3\sqrt{3}}{2}-\dfrac{3}{2}i$

79.

Answer.

$3(\cos\theta+i\sin \theta),$ for $\theta=\dfrac{\pi}{6},~$ $\dfrac{\pi}{2},~$ $\dfrac{5\pi}{6},~$ $\dfrac{7\pi}{6},~$ $\dfrac{3\pi}{2},~$ $\dfrac{11\pi}{6}$

81.

Answer.

$\sqrt{2}(\cos(\theta)+i\sin (\theta)),$ for $\theta=\dfrac{\pi}{3},~$ $\dfrac{2\pi}{3},~$ $\dfrac{4\pi}{3},~$ $\dfrac{5\pi}{3}$

Prev Top Next

\(x\)	\(-5\)	\(-4\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(y\)	\(0\)	\(\pm 3\)	\(\pm 4\)	\(\pm \sqrt{21}\)	\(\pm 2\sqrt{6} \)	\(\pm 5\)	\(\pm 2\sqrt{6}\)	\(\pm \sqrt{21}\)	\(\pm 4\)	\(\pm 3 \)	\(0\)

\(~~~~\)	sin(\theta)	cos(\theta)	tan(\theta)
\(\theta\)	\(\frac{3}{5}\)	\(\frac{4}{5}\)	\(\frac{3}{4}\)
\(\phi\)	\(\frac{4}{5}\)	\(\frac{3}{5}\)	\(\frac{4}{3}\)

\(~~~~\)	sin(\theta)	cos(\theta)	tan(\theta)
\(\theta\)	\(\frac{1}{\sqrt{5}}\)	\(\frac{2}{\sqrt{5}}\)	\(\frac{1}{2}\)
\(\phi\)	\(\frac{2}{\sqrt{5}}\)	\(\frac{1}{\sqrt{5}}\)	\(2\)

\(\theta\)	\(~~~0\degree~~~\)	\(~~~30\degree~~~\)	\(~~~45\degree~~~\)	\(~~~60\degree~~~\)	\(~~~90\degree~~~\)
\(\sin (\theta)\)	\(0\)	\(\dfrac{1}{2} \)	\(\dfrac{\sqrt{2}}{2} \)	\(\dfrac{\sqrt{3}}{2} \)	\(1\)
\(\cos (\theta)\)	\(1\)	\(\dfrac{\sqrt{3}}{2} \)	\(\dfrac{\sqrt{2}}{2} \)	\(\dfrac{1}{2} \)	\(0\)
\(\tan (\theta)\)	\(0\)	\(\dfrac{1}{\sqrt{3}} \)	\(1\)	\(\sqrt{3}\)	undefined

\(\theta\)	\(81\degree\)	\(82\degree\)	\(83\degree\)	\(84\degree\)	\(85\degree\)	\(86\degree\)	\(87\degree\)	\(88\degree\)	\(89\degree\)
\(\tan (\theta)\)	\(6.314\)	\(7.115\)	\(8.144\)	\(9.514\)	\(11.43\)	\(14.301\)	\(19.081\)	\(28.636\)	\(57.29\)

\(\theta\)	\(0\degree\)	\(90\degree\)	\(180\degree\)	\(270\degree\)	\(360\degree\)
\(f(\theta)\)	\(0\)	\(1\)	\(0\)	\(-1\)	\(0\)

\(\theta\)	\(99\degree\)	\(98\degree\)	\(97\degree\)	\(96\degree\)	\(95\degree\)	\(94\degree\)	\(93\degree\)	\(92\degree\)	\(91\degree\)
\(\tan (\theta)\)	\(-6.314\)	\(-7.115\)	\(-8.144\)	\(-9.514\)	\(-11.43\)	\(-14.301\)	\(-19.081\)	\(-28.636\)	\(-57.29\)

Radians	\(0\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{3\pi}{4}\)	\(\pi\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2 \pi\)
Degrees	\(0\degree\)	\(45\degree\)	\(90\degree\)	\(135\degree\)	\(180\degree\)	\(225\degree\)	\(270\degree\)	\(315\degree\)	\(360\degree\)

Radians	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)
Degrees	\(30\degree\)	\(45\degree\)	\(60\degree\)

Radians	\(\dfrac{7\pi}{6}\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{4\pi}{3}\)
Degrees	\(210\degree\)	\(225\degree\)	\(240\degree\)

\(\hphantom{0000}\)	a	b	c	d
\(t\)	\(\dfrac{\pi}{4}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{4}\)	\(\dfrac{7\pi}{4}\)
\(x\)	\(\dfrac{1}{\sqrt{2}}\)	\(\dfrac{-1}{\sqrt{2}}\)	\(\dfrac{-1}{\sqrt{2}}\)	\(\dfrac{1}{\sqrt{2}}\)
\(y\)	\(\dfrac{1}{\sqrt{2}}\)	\(\dfrac{1}{\sqrt{2}}\)	\(\dfrac{-1}{\sqrt{2}}\)	\(\dfrac{-1}{\sqrt{2}}\)

\(~\theta~\)	\(~~~\sin (\theta)~~~\)	\(~~~\cos (\theta)~~~\)	\(~~~\tan (\theta)~~~\)
\(\dfrac{7\pi}{6}\)	\(\dfrac{-1}{2}\)	\(\dfrac{-\sqrt{3}}{2}\)	\(\dfrac{1}{\sqrt{3}}\)
\(\dfrac{5\pi}{4}\)	\(\dfrac{-1}{\sqrt{2}}\)	\(\dfrac{-1}{\sqrt{2}}\)	\(1\)
\(\dfrac{4\pi}{3}\)	\(\dfrac{-\sqrt{3}}{2}\)	\(\dfrac{-1}{2}\)	\(\sqrt{3}\)

\(t\)	\(2t\)	\(\cos (2t)\)	\(-5\cos (2t)\)	\(2-5\cos (2t)\)
\(0\)	\(0\)	\(1\)	\(-5\)	\(-3\)
\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(0\)	\(0\)	\(2\)
\(\dfrac{\pi}{2}\)	\(\pi\)	\(-1\)	\(5\)	\(7\)
\(\dfrac{3\pi}{4}\)	\(\dfrac{3\pi}{2}\)	\(0\)	\(0\)	\(2\)
\(\pi\)	\(2\pi\)	\(1\)	\(-5\)	\(-3\)

\(t\)	\(\dfrac{t}{2}\)	\(\cos \left(\dfrac{t}{2}\right)\)	\(3\cos \left(\dfrac{t}{2}\right)\)	\(1+3\cos \left(\dfrac{t}{2}\right)\)
\(0\)	\(0\)	\(1\)	\(3\)	\(4\)
\(\pi\)	\(\dfrac{\pi}{2}\)	\(0\)	\(0\)	\(1\)
\(2\pi\)	\(\pi\)	\(-1\)	\(-3\)	\(-2\)
\(3\pi\)	\(\dfrac{3\pi}{2}\)	\(0\)	\(0\)	\(1\)
\(4\pi\)	\(2\pi\)	\(1\)	\(3\)	\(4\)

\(t\)	\(\dfrac{t}{3}\)	\(\sin \left(\dfrac{t}{3}\right)\)	\(2\sin \left(\dfrac{t}{3}\right)\)	\(-3+2\sin \left(\dfrac{t}{3}\right)\)
\(0\)	\(0\)	\(0\)	\(0\)	\(-3\)
\(\dfrac{3\pi}{2}\)	\(\dfrac{\pi}{2}\)	\(1\)	\(2\)	\(-1\)
\(3\pi\)	\(\pi\)	\(0\)	\(0\)	\(-3\)
\(\dfrac{9\pi}{2}\)	\(\dfrac{3\pi}{2}\)	\(-1\)	\(-2\)	\(-5\)
\(6\pi\)	\(2\pi\)	\(0\)	\(0\)	\(-3\)

\(\theta\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
\(s\)	\(4\)	\(8\)	\(12\)	\(16\)	\(20\)	\(24\)

\(x\)	\(-1\)	\(\frac{-\sqrt{3}}{2}\)	\(\frac{-\sqrt{2}}{2}\)	\(\frac{-1}{2}\)	\(0\)	\(\frac{1}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{3}}{2}\)	\(1\)
\(\cos^{-1}(x)\)	\(\pi\)	\(\frac{5\pi}{6} \)	\(\frac{3\pi}{4} \)	\(\frac{2\pi}{3} \)	\(\frac{\pi}{2} \)	\(\frac{\pi}{3} \)	\(\frac{\pi}{4} \)	\(\frac{\pi}{6} \)	\(0 \)

\(x\)	\(-\sqrt{3}\)	\(-1\)	\(\frac{-1}{\sqrt{3}}\)	\(0\)	\(\frac{1}{\sqrt{3}}\)	\(1\)	\(\sqrt{3}\)
\(\cos^{-1}(x)\)	\(\frac{-\pi}{2} \)	\(\frac{-\pi}{3} \)	\(\frac{-\pi}{6} \)	\(0 \)	\(\frac{\pi}{6} \)	\(\frac{\pi}{4} \)	\(\frac{\pi}{3} \)

\(x\)	\(\dfrac{-\pi}{4}\)	\(\dfrac{-\pi}{8}\)	\(0\)	\(\dfrac{\pi}{8}\)	\(\dfrac{\pi}{4}\)
\(\tan 2x\)	undef	\(-1\)	\(0\)	\(1\)	undef

\(x\)	\(\dfrac{-\pi}{6}\)	\(\dfrac{-\pi}{12}\)	\(0\)	\(\dfrac{\pi}{12}\)	\(\dfrac{\pi}{6}\)
\(4+2\tan 3x\)	undef	\(2\)	\(0\)	\(6\)	undef

\(x\)	\(-2\pi\)	\(-\pi\)	\(0\)	\(\pi\)	\(2\pi\)
\(3-\tan \left(\dfrac{x}{4}\right)\)	undef	\(4\)	\(0\)	\(2\)	undef

\(x\)	\(-\pi\)	\(\dfrac{-3\pi}{4}\)	\(\dfrac{-\pi}{2}\)	\(\dfrac{-\pi}{4}\)	\(0\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{3\pi}{4}\)	\(\pi\)
\(f(x)\)	\(0\)	\(1\)	undef	\(-1\)	\(0\)	\(1\)	undef	\(-1\)	\(0\)
\(g(x)\)	\(1\)	undef	\(-1\)	\(0\)	\(1\)	undef	\(-1\)	\(0\)	\(1\)

\(x\)	\(x+\dfrac{\pi}{6}\)	\(\cos\left(x+\dfrac{\pi}{6}\right) \)	\(-2\cos\left(x+\dfrac{\pi}{6}\right)\)
\(\dfrac{-7\pi}{6}\)	\(-\pi\)	\(-1\)	\(2\)
\(\dfrac{-2\pi}{3}\)	\(\dfrac{-\pi}{2}\)	\(0\)	\(0\)
\(\dfrac{-\pi}{6}\)	\(0\)	\(1\)	\(-2\)
\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(0\)	\(0\)
\(\dfrac{5\pi}{6}\)	\(\pi\)	\(-1\)	\(2\)
\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(0\)	\(0\)
\(\dfrac{11\pi}{6}\)	\(2\pi\)	\(1\)	\(-2\)

\(x\)	\(2x\)	\(2x-\dfrac{\pi}{3} \)	\(\cos\left(2x-\dfrac{\pi}{3}\right)\)
\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(0\)	\(1\)
\(\dfrac{5\pi}{12}\)	\(\dfrac{5\pi}{6}\)	\(\dfrac{\pi}{2}\)	\(0\)
\(\dfrac{2\pi}{3}\)	\(\dfrac{4\pi}{3}\)	\(\pi\)	\(-1\)
\(\dfrac{11\pi}{12}\)	\(\dfrac{11\pi}{6}\)	\(\dfrac{3\pi}{2}\)	\(0\)
\(\dfrac{7\pi}{6}\)	\(\dfrac{7\pi}{3}\)	\(2\pi\)	\(1\)

\(x\)	\(\pi x\)	\(\pi x+\dfrac{\pi}{3} \)	\(\sin\left(\pi x+\dfrac{\pi}{3}\right)\)
\(\dfrac{-1}{3}\)	\(\dfrac{-\pi}{3}\)	\(0\)	\(0\)
\(\dfrac{1}{6}\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{2}\)	\(1\)
\(\dfrac{2}{3}\)	\(\dfrac{2\pi}{3}\)	\(\pi\)	\(0\)
\(\dfrac{7}{6}\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{3\pi}{2}\)	\(-1\)
\(\dfrac{5}{3}\)	\(\dfrac{5\pi}{3}\)	\(2\pi\)	\(0\)

\(x\)	\(\dfrac{x}{2}\)	\(\dfrac{x}{2}-\dfrac{\pi}{6} \)	\(\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)\)	\(3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4\)
\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{6}\)	\(0\)	\(0\)	\(4\)
\(\dfrac{4\pi}{3}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(1\)	\(7\)
\(\dfrac{7\pi}{3}\)	\(\dfrac{7\pi}{6}\)	\(\pi\)	\(0\)	\(3\)
\(\dfrac{10\pi}{3}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(-1\)	\(1\)
\(\dfrac{13\pi}{3}\)	\(\dfrac{13\pi}{6}\)	\(2\pi\)	\(0\)	\(4\)

\(x\)	\(\dfrac{x}{2}\)	\(\dfrac{x}{2}+\dfrac{\pi}{6} \)	\(\sin\left(\dfrac{x}{2}+\dfrac{\pi}{6}\right)\)
\(\dfrac{-2\pi}{3}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{-\pi}{6}\)	\(\dfrac{-1}{2}\)
\(\dfrac{-\pi}{3}\)	\(\dfrac{-\pi}{6}\)	\(0\)	\(0\)
\(0\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{1}{2}\)
\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{12}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{1}{\sqrt{2}}\)
\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\sqrt{3}}{2}\)
\(\dfrac{2\pi}{3}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(1\)
\(\pi\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{\sqrt{3}}{2}\)

\(x\)	\(\dfrac{\pi}{30}x \)	\(\cos\left(\dfrac{\pi}{30}x\right)\)	\(20-5\cos\left(\dfrac{\pi}{30}x\right)\)
\(-5\)	\(\dfrac{-\pi}{6}\)	\(\dfrac{\sqrt{3}}{2}\)	\(20-\dfrac{\sqrt{3}}{2}\)
\(0\)	\(0\)	\(1\)	\(15\)
\(5\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\sqrt{3}}{2}\)	\(20-\dfrac{\sqrt{3}}{2}\)
\(10\)	\(\dfrac{\pi}{3}\)	\(\dfrac{1}{2}\)	\(17.5\)
\(15\)	\(\dfrac{\pi}{2}\)	\(0\)	\(20\)
\(50\)	\(\pi\)	\(-1\)	\(25\)

Appendix A Answers to Selected Exercises and Homework Problems

1 Triangles and Circles1.1 Angles and Triangles Homework 1.1

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

21.

23.

25.

27.

29.

31.

33.

35.

37.

39.

41.

43.

45.

47.

1.2 Similar Triangles Homework 1.2

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

21.

23.

25.

27.

29.

31.

33.

35.

37.

39.

1.3 Circles Homework 1.3

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

21.

23.

25.

27.

29.

31.

33.

35.

37.

39.

41.

43.

45.

47.

49.

51.

53.

55.

1.4 Chapter 1 Summary and Review Chapter 1 Review Problems

1.

3.

5.

1 Triangles and Circles
1.1 Angles and Triangles
Homework 1.1

1.2 Similar Triangles
Homework 1.2

1.3 Circles
Homework 1.3

1.4 Chapter 1 Summary and Review
Chapter 1 Review Problems

2 The Trigonometric Ratios
2.1 Side and Angle Relationships
Homework 2.1

2.2 Right Triangle Trigonometry
Homework 2.2