Skip to main content

Section 2.5 The Absolute Value Function

Subsection 1. Use interval notation

Recall that square brackets on an interval mean that the endpoints are included, and round brackets mean that the endpoints are not included.

Subsubsection Example

Example 2.51.

Write each set with interval notation, and graph the set on a number line.

  1. \(\displaystyle 3 \le x \lt 6\)
  2. \(\displaystyle x \ge -9\)
  3. \(\displaystyle x \le 1~\text{or}~x\gt 4\)
  4. \(\displaystyle -8 \lt x \le 5~\text{or}~-1\le x \lt 3\)
Solution

  1. \([3,6).\) This is called a half-open or half-closed interval. \(3\) is included in the interval, but \(6\) is not included.

    interval

  2. \([-9, \infty).\) We use round brackets next to the symbol \(\infty\) because \(\infty\) is not a specific number and is not included in the set.

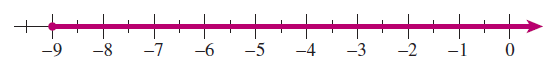
    interval

  3. \((-\infty,1] \cup (4, \infty).\) The word “or” describes the union of two sets. The symbol \(~\cup~\) is used for union.

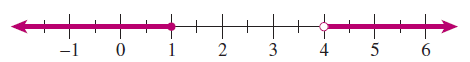
    interval

  4. \(\displaystyle (-8,-5] \cup [-1,3).\)

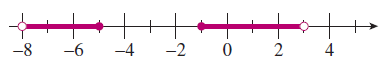
    interval

Subsubsection Exercise

Write each set with interval notation, and graph the set on a number line.

  1. \(\displaystyle -5 \lt x \le 3\)
  2. \(\displaystyle -6 \lt x \lt \infty\)
  3. \(\displaystyle x \lt -3 ~\text{or}~ x\ge -1\)
  4. \(\displaystyle -6 \le x \lt-4 ~\text{or}~ -2 \lt x \le 0\)
Answer
  1. \((-5,-3]\)
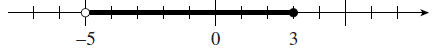
    interval
  2. \((-6, \infty)\)
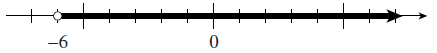
    interval
  3. \((-\infty,-3) \cup [-1,\infty)\)
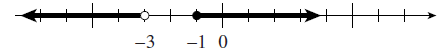
    interval
  4. \([-6,-4) \cup (-2,0]\)
    interval

Subsection 2. Solve compound inequalities

A compund inequality is one where the algebraic expression is bounded both above and below.

Subsubsection Example

Example 2.53.

Solve the inequality \(~-3 \lt 2x-5 \le 6~\) and write your solution with interval notation.

Solution

To isolate \(x\text{,}\) we first add 5 on each side of the inequality symbols.

\begin{align*} -3 \amp \lt 2x-5 \le 6 \amp\amp \blert{\text{Add 5 on all three sides.}}\\ 2 \amp \lt 2x~~ \le 11 \amp\amp \blert{\text{Divide each side by 2.}}\\ 1 \amp \lt x \le \dfrac{11}{2} \end{align*}

The solutions are all real numbers greater than 1 but less than or equal to \(\dfrac{11}{2}\text{.}\) In interval notation, we write \(~\left(1, \dfrac{11}{2}\right]\text{.}\)

Subsubsection Exercises

Solve the inequality \(~~~23 \gt 9-2b \ge 13~~~\) and write your solution with interval notation.

Answer
\((-7,-2]\)

Solve the inequality \(~~~-8 \le \dfrac{5w+3}{4} \lt -3~~~\) and write your solution with interval notation.

Answer
\([-7,-3)\)

Subsection 3. Simplify absolute value functions

The piecewise definition of the absolute value function is

\begin{equation*} f(x) = \begin{cases} x \amp \text{if} ~~x\ge 0\\ -x \amp \text{if} ~~x\lt 0 \end{cases} \end{equation*}

To write the absolute value of some other algebraic expression, we replace \(x\) by the expression wherever \(x\) appears.

Subsubsection Example

Example 2.56.

Simplify the function \(~f(x)=|2x-8|~\) as a piecewise defined function.

Solution

We use the definition of absolute value and replace \(x\) by \(2x-8\text{.}\)

\begin{equation*} f(x) = \begin{cases} 2x-8 \amp \text{if} ~~2x-8\ge 0\\ -(2x-8) \amp \text{if} ~~2x-8\lt 0 \end{cases} \end{equation*}

Then we simplify each expression.

\begin{equation*} f(x) = \begin{cases} 2x-8 \amp \text{if} ~~x\ge 4\\ 8-2x \amp \text{if} ~~x\lt 4 \end{cases} \end{equation*}

Subsubsection Exercises

Simplify the function \(~f(x)=|6-3x|~\) as a piecewise defined function.

Answer
\begin{equation*} f(x) = \begin{cases} 6-3x \amp \text{if} ~~x\le 2\\ 3x-6 \amp \text{if} ~~x\gt 2 \end{cases} \end{equation*}

Simplify the function \(~f(x)=|1+4x|~\) as a piecewise defined function.

Answer
\begin{equation*} f(x) = \begin{cases} 1+4x \amp \text{if} ~~x\ge \dfrac{-1}{4}\\ -1-4x \amp \text{if} ~~x\lt \dfrac{-1}{4} \end{cases} \end{equation*}