Elementary Algebra Operations on Radicals

Section 9.4 Operations on Radicals

Subsection Products

We have used the product rule for radicals,

\begin{equation*} \sqrt{ab} = \sqrt{a} \sqrt{b} \end{equation*}

to simplify square roots. We can also use the product rule to multiply radicals together.

Product Rule.

\begin{equation*} \text{If}~~a, ~b \ge 0,~~\text{then}~~~~\blert{\sqrt{a} \sqrt{b}=\sqrt{ab}} \end{equation*}

For example,

\begin{equation*} \sqrt{2} \cdot \sqrt{3}=\sqrt{6}~~~~~~\text{and}~~~~~ \sqrt{5} \cdot \sqrt{x}=\sqrt{5x} \end{equation*}

Example 9.34.

Find the product and simplify $\sqrt{2x}\sqrt{10xy}$

Solution.

First, we apply the product rule.

\begin{align*} \sqrt{2x}\sqrt{10xy} \amp =\sqrt{20x^2y}~~~~~~~~~~\blert{\text{Factor out perfect squares.}}\\ \amp = \sqrt{4x^2}\sqrt{5y} = 2x\sqrt{5y} \end{align*}

Reading Questions Reading Questions

1.

Which of these statements is correct:

$\displaystyle \sqrt{x^2+4} = \sqrt{x^2}+\sqrt{4}$
$\displaystyle \sqrt{4x^2} = \sqrt{4}\sqrt{x^2}$
$\displaystyle \sqrt{x^2-4} = \sqrt{x^2}-\sqrt{4}$
$\displaystyle \sqrt{\dfrac{x^2}{4}} = \dfrac{\sqrt{x^2}}{\sqrt{4}}$

Answer.

(b) and (d)

We use the distributive law to remove parentheses from products involving radicals. Compare the product involving radicals on the left with the more familiar use of the distributive law on the right.

\begin{equation*} 6(\sqrt{3} + \sqrt{2}) = 6\sqrt{3} + 6\sqrt{2}~~~~~~~~6(x+y)=6x+6y \end{equation*}

Example 9.35.

Multiply $~~5(3x+4\sqrt{2})$

Solution.

Apply the distributive law to find

\begin{equation*} \blert{5}(3x+4\sqrt{2}) = \blert{5} \cdot 3x + \blert{5} \cdot 4\sqrt{2} = 15x + 20\sqrt{2} \end{equation*}

Reading Questions Reading Questions

2.

Explain why this statement is incorrect: $5 \cdot 4\sqrt{2} = 20 \cdot 5 \sqrt{2}$

Answer.

Because $4\sqrt{2}$ is only one term.

In the next example, we use the distributive law along with the product rule to simplify the product.

Example 9.36.

Multiply $~~2\sqrt{5}(3+\sqrt{3})$

Solution.

Apply the distributive law to obtain

\begin{align*} \blert{2\sqrt{5}}(3+\sqrt{3}) \amp =\blert{2\sqrt{5}} \cdot 3 + \blert{2\sqrt{5}} \cdot \sqrt{3}\\ \amp ~~~~~~~~~~\blert{\text{Apply the product rule to the second term.}}\\ \amp = 6\sqrt{5} + 2\sqrt{15} \end{align*}

Caution 9.37.

Note the difference between the products

\begin{equation*} \sqrt{5} \cdot 3 = 3\sqrt{5} ~~~~~\text{and}~~~~~ \sqrt{5} \cdot \sqrt{3} = \sqrt{15} \end{equation*}

The rule $\sqrt{a}\sqrt{b} = \sqrt{ab}$ applies to the second product, but not the first.

Reading Questions Reading Questions

3.

Explain how to multiply $(3\sqrt{2})(4\sqrt{2})$

Answer.

Multiply $3 \cdot 4$ to get $12\text{,}$ multiply $\sqrt{2}\sqrt{2}$ to get $\sqrt{10}\text{,}$ write the product $12\sqrt{10}\text{.}$

To multiply binomials, we use the FOIL method.

Example 9.38.

Multiply $~~\left(2+\sqrt{3}\right)\left(1-2\sqrt{3}\right)\text{,}$ then simplify.

Solution.

\begin{align*} \left(2+\sqrt{3}\right)\left(1-2\sqrt{3}\right) \amp = 2 \cdot 1-2 \cdot 2\sqrt{3}+\sqrt{3} \cdot 1-\sqrt{3}\cdot 2\sqrt{3}\\ \amp ~~~~~~~~~~\blert{\text{F}~~~~~~~~~~~~~~\text{O}~~~~~~~~~~~~~~~~~~\text{I}~~~~~~~~~~~~~~~~~~\text{L}}\\ \amp = 2-4\sqrt{3}+\sqrt{3}-2\cdot 3 ~~~~~~~~\blert{\text{Note that}~~\sqrt{3} \cdot \sqrt{3} = 3}\\ \amp = 2-4\sqrt{3}+\sqrt{3}-6 ~~~~~~~~~~~~~~\blert{\text{Combine like terms.}}\\ \amp = -4-3\sqrt{3} \end{align*}

Reading Questions Reading Questions

4.

Explain why $\sqrt{b}\sqrt{b}=b$

Answer.

The square root of $b$ is a number that, when multiplied by itself, gives $b\text{.}$

Subsection Quotients

We use the quotient rule to simplify square roots of fractions by writing $\sqrt{\dfrac{a}{b}} = \dfrac{\sqrt{a}}{\sqrt{b}}\text{.}$ We can also use the quotient rule to simplify quotients of square roots.

Quotient Rule.

\begin{equation*} \text{If}~~a \ge 0~~\text{and}~~b \gt 0,~~\text{then}~~~~\blert{ \dfrac{\sqrt{a}}{\sqrt{b}}=\sqrt{\dfrac{a}{b}} } \end{equation*}

Example 9.39.

Simplify $~~\dfrac{2\sqrt{30a}}{\sqrt{6a}}$

Solution.

We use the quotient rule to write the expression as a single radical. Then we simplify the fraction inside the radical.

\begin{align*} \dfrac{2\sqrt{30a}}{\sqrt{6a}} \amp = 2\sqrt{\dfrac{30a}{6a}}~~~~~~~~\blert{\text{Reduce the fraction.}}\\ \amp = 2\sqrt{5} \end{align*}

Reading Questions Reading Questions

5.

Is it true that we can only simplify a product or quotient of radicals if they are like radicals?

Answer.

No.

Subsection Fractions

When we solve quadratic equations, the solutions are often fractions that involve square roots. Many such fractions can be simplified using properties of radicals.

Example 9.40.

One of the solutions of the equation $4x^2-8x=1$ is $\dfrac{8+\sqrt{80}}{8}\text{.}$ Simplify this radical expression.

Solution.

First, simplify the square root: $\sqrt{80}=\sqrt{16 \cdot 5} = 4\sqrt{5}\text{.}$ Thus,

\begin{align*} \dfrac{8+\sqrt{80}}{8} \amp = \dfrac{8+4\sqrt{5}}{8} \amp \amp \blert{\text{Factor numerator and denominator.}}\\ \amp = \dfrac{\cancel{\blert{4}}(2+\sqrt{5})}{\cancel{\blert{4}} \cdot 2} \amp \amp \blert{\text{Divide out common factors.}}\\ \amp = \dfrac{2+\sqrt{5}}{2} \end{align*}

Caution 9.41.

In Example 9.40, note that

\begin{equation*} 8+4\sqrt{5} \not= 12\sqrt{5} \end{equation*}

because $8$ and $4\sqrt{5}$ are not like terms. Also note that

\begin{equation*} \dfrac{8+\sqrt{80}}{8} \not= \sqrt{80} \end{equation*}

Because 8 is a term of the numerator, not a factor, we cannot cancel the 8's.

Reading Questions Reading Questions

6.

Which of these cannot be reduced: $~~\dfrac{4+\sqrt{6}}{2}~~$ or $~~\dfrac{4\sqrt{6}}{2}~~$ Why?

Answer.

$~~\dfrac{4+\sqrt{6}}{2}~~\text{.}$ The numerator cannot be factored.

We can add or subtract fractions involving radicals.

Example 9.42.

Subtract $~~\dfrac{1}{2}-\dfrac{\sqrt{3}}{3}$

Solution.

The LCD for the two fractions is 6. We build each fraction to an equivalent one with denominator 6, then combine the numerators.

\begin{align*} \dfrac{1}{2}-\dfrac{\sqrt{3}}{3} \amp = \dfrac{1 \cdot \blert{3}}{2\cdot \blert{3}}-\dfrac{\sqrt{3}\cdot \blert{2}}{3\cdot \blert{2}}\\ \amp = \dfrac{3}{6}-\dfrac{2\sqrt{3}}{6} = \dfrac{3-2\sqrt{3}}{6} \end{align*}

Subsection Rationalizing the Denominator

For some applications, it is easier to work with expressions that do not have radicals in the denominators of fractions. For example, the fraction $~\dfrac{\sqrt{2}}{\sqrt{3}}~$ is equivalent to

\begin{equation*} \dfrac{\sqrt{2}\cdot \blert{\sqrt{3}}}{\sqrt{3}\cdot \blert{\sqrt{3}}} = \dfrac{\sqrt{6}}{3} \end{equation*}

We multiplied the numerator and denominator by $\sqrt{3}\text{,}$ the same root that appeared in the denominator originally, and thus eliminated the radical from the denominator. This process is called rationalizing the denominator.

Example 9.43.

Rationalize the denominator of $~~\dfrac{10}{\sqrt{50}}$

Solution.

We simplify the radical before attempting to rationalize the denominator.

\begin{equation*} \dfrac{10}{\sqrt{50}} = \dfrac{10}{5\sqrt{2}}=\dfrac{2}{\sqrt{2}} \end{equation*}

Now we multiply top and bottom of the fraction by $\sqrt{2}\text{.}$

\begin{equation*} \dfrac{2 \cdot \blert{\sqrt{2}}}{\sqrt{2}\cdot \blert{\sqrt{2}}} = \dfrac{2\sqrt{2}}{2} = \sqrt{2} \end{equation*}

Reading Questions Reading Questions

7.

What does it mean to rationalize the denominator?

Answer.

To eliminate radicals from the denominator.

8.

What should you do before trying to rationalize a denominator?

Answer.

Simplify the radicals.

Subsection Skills Warm-Up

Exercises Exercises

Exercise Group.

Each simplification is incorrect. Give the correct simplification, or write c.b.s. if the expression cannot be simplified.

1.

$2+4\sqrt{5} \rightarrow 6\sqrt{5}$

2.

$\dfrac{2+3\sqrt{5}}{2} \rightarrow 3\sqrt{5}$

3.

$3\sqrt{5}+3\sqrt{2} \rightarrow 3\sqrt{7}$

4.

$\dfrac{4+\sqrt{6}}{2} \rightarrow 2+\sqrt{3}$

5.

$2(3\sqrt{5}) \rightarrow 6\sqrt{10}$

6.

$2(3+\sqrt{5}) \rightarrow 6+\sqrt{10}$

7.

$(3\sqrt{5})(4\sqrt{5}) \rightarrow 12\sqrt{5}$

8.

$3\sqrt{5}+4\sqrt{5} \rightarrow 7\sqrt{10}$

Subsubsection Answers to Skills Warm-Up

c.b.s.
c.b.s.
c.b.s.
c.b.s.
$\displaystyle 6\sqrt{5}$
$\displaystyle 6+2\sqrt{5}$
$\displaystyle 60$
$\displaystyle 7\sqrt{5}$

Subsection

Subsubsection Activity 1: Products and Quotients

Exercises Exercises

1.

Find the product and simplify $~~(3x\sqrt{6x})(y\sqrt{15xy})$

2.

Multiply $~~2a(2\sqrt{3}-\sqrt{a})$

3.

Multiply $~~3\sqrt{x}(\sqrt{2x}-3x)$

4.

Expand and simplify $~~(\sqrt{2}-2\sqrt{b})^2$

5.

Simplify $~~\dfrac{3ab\sqrt{75a^3b}}{\sqrt{6ab^5}}$

Subsubsection Activity 2: Fractions with Radicals

Exercises Exercises

1.

Add $~~\dfrac{\sqrt{x}}{3}+\dfrac{\sqrt{2}}{x}$

2.

Rationalize the denominator of $~~\dfrac{8}{\sqrt{x}}$

Subsubsection Activity 3: Application

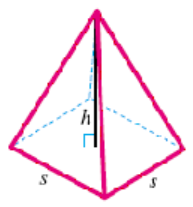
In this Activity we use a formula for the surface area of a pyramid with a square base, as shown in the figure at right.

The pyramid has five faces, namely, the square base and four triangular sides. We know the height, $h\text{,}$ of the pyramid, and the length, $s\text{,}$ of the base.

To calculate the surface area of the pyramid, we add the area of its base and the areas of the four triangular faces.

\begin{align*} S \amp = \text{(area of base)}~+~4 ~\text{(area of triangular face)}\\ \amp = s^2 + 4 \cdot \dfrac{1}{4}s\sqrt{4h^2+s^2}\\ \amp = s^2 + s\sqrt{4h^2+s^2} \end{align*}

Use the formula given above to find the surface area of the Sun Pyramid in Mexico. The pyramid is 210 feet high and has a square base 689 feet on each side.

Challenge: Can you verify the expression for the area of a triangular face of the pyramid? Begin by finding the altitude of the face.

Subsubsection Wrap-Up

Objectives.

In this Lesson we practiced the following skills:

Simplifying products involving radicals
Simplifying quotients of radicals
Rationalizing the denominator

Questions.

In Activity 1 Problem 5, why don't we start by rationalizing the denominator?
Explain why $~\dfrac{\sqrt{6x}}{3}~$ is not equivalent to $~\sqrt{2x}\text{.}$
In Activity 3, why don't we simplify $~\sqrt{4h^2+s^2}~$ to $~2h+s\text{?}$

Subsection Homework Preview

Exercises Exercises

Exercise Group.

Find the product and simplify.

1.

$(3a\sqrt{12a})(2b\sqrt{6ab^3})$

2.

$5t(3t^3-2t\sqrt{2t})$

3.

$4\sqrt{3x}(2x\sqrt{6x}+3\sqrt{x})$

4.

$(3-\sqrt{k})(4+2\sqrt{k})$

Exercise Group.

Find the quotient and simplify.

5.

$\dfrac{\sqrt{10}}{\sqrt{45}}$

6.

$\dfrac{\sqrt{72x^3}}{\sqrt{36x}}$

7.

Subtract $~~\dfrac{4+\sqrt{2}}{3}-\dfrac{\sqrt{2}}{2}$

8.

Rationalize the denominator $~~\dfrac{3}{\sqrt{12x}}$

Subsubsection Answers to Homework Preview

$\displaystyle 36a^2b^2\sqrt{2b}$
$\displaystyle 15t^4-10t^2\sqrt{2t}$
$\displaystyle 24x^2\sqrt{2}+12x\sqrt{3}$
$\displaystyle 12+2\sqrt{k}-2k$
$\displaystyle \dfrac{\sqrt{2}}{3}$
$\displaystyle x\sqrt{2}$
$\displaystyle \dfrac{8-\sqrt{2}}{6}$
$\displaystyle \dfrac{\sqrt{3x}}{2x}$

Exercises Homework 9.4

Exercise Group.

For Problems 1–3, simplify the product.

1.

$\sqrt{8}\sqrt{2}$

2.

$\sqrt{2x}\sqrt{3x}$

3.

$\left(3\sqrt{8a}\right)\left(a\sqrt{18a}\right)$

Exercise Group.

For Problems 4–6, multiply.

4.

$\sqrt{2}(3+\sqrt{3})$

5.

$\sqrt{5}(4+2\sqrt{15})$

6.

$\left(2\sqrt{p}\right)\left(\sqrt{2p}-p\sqrt{2}\right)$

Exercise Group.

For Problems 7–10, multiply.

7.

$(3+\sqrt{2})(1-\sqrt{2})$

8.

$(4-\sqrt{a})(4+\sqrt{a})$

9.

$(2+\sqrt{3})^2$

10.

$(2\sqrt{w}+\sqrt{5})(\sqrt{w}-2\sqrt{5})$

Exercise Group.

For Problems 11–13, simplify the quotient.

11.

$\dfrac{\sqrt{18}}{\sqrt{2}}$

12.

$\dfrac{\sqrt{75x^3}}{\sqrt{3x}}$

13.

$\dfrac{\sqrt{48b}}{\sqrt{27b}}$

Exercise Group.

For Problems 14–16, reduce if possible.

14.

$\dfrac{9-3\sqrt{5}}{3}$

15.

$\dfrac{-8+\sqrt{8}}{4}$

16.

$\dfrac{6a-\sqrt{18}}{6a}$

Exercise Group.

For Problems 17–20, write the expression as a single fraction in simplest form.

17.

$\dfrac{5}{4}+\dfrac{3\sqrt{2}}{2}$

18.

$\dfrac{3}{2a}+\dfrac{\sqrt{3}}{6a}$

19.

$\dfrac{3\sqrt{3}}{2}+3$

20.

$\dfrac{3}{4}-2\sqrt{y}$

Exercise Group.

For Problems 21–24, find and correct the error in the calculation.

21.

$8\sqrt{7}-2\sqrt{5} \rightarrow 6\sqrt{2}$

22.

$6\sqrt{8} \rightarrow \sqrt{48}$

23.

$\dfrac{5-10\sqrt{3}}{5} \rightarrow -10\sqrt{3}$

24.

$\sqrt{x^2+16} \rightarrow x+4$

Exercise Group.

For Problems 25–28, rationalize the denominator.

25.

$\dfrac{5}{\sqrt{2}}$

26.

$\dfrac{a\sqrt{2}}{\sqrt{a}}$

27.

$\dfrac{b\sqrt{21}}{\sqrt{3b}}$

28.

$\sqrt{\dfrac{7x}{12}}$

29.

Write an expression for the height of an equilateral triangle of side $w\text{.}$ (See the figure at right.)
Write an expression for the area of the triangle in part (a).

$triangle$

30.

Write an expression in terms of $k$ for the height of the pyramid shown at right.
Write an expressionin terms of $k$ for the area of the pyramid.

Exercise Group.

For Problems 31–33, verify by substitution that the given value is a solution of the equation.

31.

$t^2-2\sqrt{3}t+3=0,~~~~~~~~t=\sqrt{3}$

32.

$s^2+1=4s,~~~~~~~~s=\sqrt{3}+2$

33.

$x^2+3x+1=0,~~~~~~~~x=\dfrac{-3+\sqrt{5}}{2}$