Subsection Horizontal Shifts
In the previous section we considered transformations of sinusoidal graphs, including vertical shifts, which change the midline of the graph, vertical stretches and compressions, which change its amplitude, and horizontal stretches and compressions, which occur when we change the period of the graph.
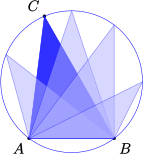
In this section we consider one more transformation, shifting the graph horizontally. The figure below shows four different transformations of the graph of \(y=\sin (x)\text{.}\)
Example 7.15.
Graph \(~f(x)=\sin (x)~\) and \(~g(x)= \sin \left(x - \dfrac{\pi}{4}\right)~\) for \(-2\pi \le x \le 2\pi\text{.}\) How is the graph of \(g\) different from the graph of \(f\text{?}\)
Solution.
The graphs are shown below. The graph of \(~g(x)= \sin \left(x - \dfrac{\pi}{4}\right)~\) has the same amplitude, midline, and period as the graph of \(~f(x)=\sin (x)\text{,}\) but the graph of \(g\) is shifted to the right by \(\dfrac{\pi}{4}\) units, compared to the graph of \(f\text{.}\)
We can see why this shift occurs by studying a table of values for the two functions.
| \(x\) |
\(0\) |
\(\dfrac{\pi}{4}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{3\pi}{4}\) |
\(\pi\) |
\(\dfrac{5\pi}{4}\) |
\(\dfrac{3\pi}{2}\) |
\(\dfrac{7\pi}{4}\) |
\(2\pi\) |
| \(f(x)\) |
\(\blert{0}\) |
\(\dfrac{\sqrt{2}}{2}\) |
\(\alert{1}\) |
\(\dfrac{\sqrt{2}}{2}\) |
\(\blert{0}\) |
\(\dfrac{-\sqrt{2}}{2}\) |
\(\alert{-1}\) |
\(\dfrac{-\sqrt{2}}{2}\) |
\(0\) |
| \(g(x)\) |
\(\dfrac{-\sqrt{2}}{2}\) |
\(\blert{0}\) |
\(\dfrac{\sqrt{2}}{2}\) |
\(\alert{1}\) |
\(\dfrac{\sqrt{2}}{2}\) |
\(\blert{0}\) |
\(\dfrac{-\sqrt{2}}{2}\) |
\(\alert{-1}\) |
\(\dfrac{-\sqrt{2}}{2}\) |
Notice that in the table, \(g\) has the same function values as \(f\text{,}\) but each one is shifted \(\dfrac{\pi}{4}\) units to the right. The same thing happens in the graph: each \(y\)-value appears \(\dfrac{\pi}{4}\) units farther to the right on \(g\) than it does on \(f\text{.}\)
Checkpoint 7.16.
Graph \(~f(x)=\cos (x)~\) and \(~g(x)= \cos \left(x + \dfrac{\pi}{4}\right)~\) for \(-2\pi \le x \le 2\pi\text{.}\) How is the graph of \(g\) different from the graph of \(f\text{?}\)
Answer.
The graph of \(g\) is shifted \(\dfrac{\pi}{4}\) units to the left of \(f\text{.}\)
The examples above illustrate the following principle.
Horizontal Shifts.
The graphs of
\begin{equation*}
y = \sin (x-h)~~~~ \text{and}~~~~ t = \cos (x-h)
\end{equation*}
are shifted horizontally compared to the graphs of \(y = \sin (x)\) and \(y = \cos (x)\text{.}\)
If \(h \gt 0\text{,}\) the graph is shifted to the right.
If \(h \lt 0\text{,}\) the graph is shifted to the left.
We can use a table of values to sketch graphs that involve horizontal shifts.
Example 7.17.
Make a table of values and sketch a graph of \(~y=-2\cos \left(x+\dfrac{\pi}{3}\right)\text{.}\)
Solution.
First notice that we can write the equation as
\begin{equation*}
y=-2\cos \left[x-\left(\dfrac{-\pi}{3}\right)\right]
\end{equation*}
so that \(h = -\dfrac{\pi}{3}\text{,}\) and we expect the graph to be shifted \(\dfrac{\pi}{3}\) units to the left compared to the graph of \(y = \cos (x)\text{.}\)
We choose convenient values for the inputs of the cosine function, namely \(x+\dfrac{\pi}{3}\text{.}\)
| \(x\) |
\(x+\dfrac{\pi}{3}\) |
\(\cos\left(x+\dfrac{\pi}{3}\right) \) |
\(y = \cos\left(x+\dfrac{\pi}{3}\right)\) |
| \(\hphantom{0000}\) |
\(\alert{0}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\alert{\dfrac{\pi}{2}}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\alert{\pi}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\alert{\dfrac{3\pi}{2}}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\alert{2\pi}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
From those values, we work backwards to \(x\) and forwards to \(y\text{.}\) (To obtain the values of \(x\text{,}\) we subtract \(\dfrac{\pi}{3}\)from the values of \(x+\dfrac{\pi}{3}\text{.}\))
| \(x\) |
\(x+\dfrac{\pi}{3}\) |
\(\cos\left(x+\dfrac{\pi}{3}\right) \) |
\(y = \cos\left(x+\dfrac{\pi}{3}\right)\) |
| \(\dfrac{-\pi}{3}\) |
\(0\) |
\(1\) |
\(-2\) |
| \(\dfrac{\pi}{6}\) |
\(\dfrac{\pi}{2}\) |
\(0\) |
\(0\) |
| \(\dfrac{2\pi}{3}\) |
\(\pi\) |
\(-1\) |
\(2\) |
| \(\dfrac{7\pi}{6}\) |
\(\dfrac{3\pi}{2}\) |
\(0\) |
\(0\) |
| \(\dfrac{5\pi}{3}\) |
\(2\pi\) |
\(1\) |
\(-2\) |
To make the graph, we’ll scale the \(x\)-axis in multiples of \(\dfrac{\pi}{6}\text{.}\) We plot the guide points \((x,y)\) from the table, and sketch a sinusoidal graph through the points. One cycle of the graph is shown below. As we expected,the graph is shifted \(\dfrac{\pi}{3}\) units to the left compared to the graph of \(~y = \cos (x)\text{.}\)
Checkpoint 7.18.
Complete the table and sketch a graph of \(~y = -2+\sin\left(x - \dfrac{\pi}{6}\right)~\) on the grid below. (Do you expect the graph to be shifted to the left or to the right, compared to the graph of \(~y = \sin (x)\text{?}\))
| \(x\) |
\(x-\dfrac{\pi}{6}\) |
\(\sin\left(x-\dfrac{\pi}{6}\right) \) |
\(y = -2+\sin\left(x-\dfrac{\pi}{6}\right)\) |
| \(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
Answer.
| \(x\) |
\(x-\dfrac{\pi}{6}\) |
\(\sin\left(x-\dfrac{\pi}{6}\right) \) |
\(y = -2+\sin\left(x-\dfrac{\pi}{6}\right)\) |
| \(\dfrac{\pi}{6}\) |
\(0\) |
\(0\) |
\(-2\) |
| \(\dfrac{2\pi}{3}\) |
\(\dfrac{\pi}{2}\) |
\(1\) |
\(-1\) |
| \(\dfrac{7\pi}{6}\) |
\(\pi\) |
\(0\) |
\(-2\) |
| \(\dfrac{5\pi}{3}\) |
\(\dfrac{3\pi}{2}\) |
\(-1\) |
\(-3\) |
| \(\dfrac{13\pi}{6}\) |
\(2\pi\) |
\(0\) |
\(-2\) |
Subsection Combining Transformations
The order in which we apply transformations to a function makes a difference in the graph. We’ll compare the graphs of the two functions
\begin{equation*}
f(x) = \sin \left[2\left(x - \dfrac{\pi}{3}\right)\right]~~~~ \text{and} ~~~~ g(x)= \sin \left(2x - \dfrac{\pi}{3}\right)
\end{equation*}
Graph the two functions for \(0 \le x \le 2\pi\text{,}\) along with \(~y = \sin (2x)~\text{,}\) as shown below. Each graph involves a horizontal shift relative to \(~y = \sin (2x)\text{,}\) but the graph of \(f\) is shifted \(\dfrac{\pi}{3}\) units to the right, while the graph of \(g\) is shifted only \(\dfrac{\pi}{6}\) units to the right. This difference occurs because of the order of the transformations.
We transform the graph of \(~y = \sin (x)~\) into the graph of \(f\) in two steps:
Step 1: First we replace \(x\) by \(2x\) to get \(~y = \sin (2x)~\text{,}\) which compresses the graph horizontally by a factor of 2. (See figure (a) below.)
Step 2: Then we replace \(x\) by \(x - \dfrac{\pi}{3}\) to get \(~f(x) = \sin \left[2\left(x - \dfrac{\pi}{3}\right)\right]\text{,}\) which shifts the graph \(\dfrac{\pi}{3}\) units to the right. (See figure (b).)
To transform the graph of \(~y = \sin (x)~\) into the graph of \(g\text{,}\) we perform the two steps in the opposite order:
Step 1: We replace \(x\) by \(x - \dfrac{\pi}{3}\) which shifts the graph \(\dfrac{\pi}{3}\) units to the right. (See figure (a).)
Step 2: Then we replace \(x\) by \(2x\) to get \(~g(x)= \sin \left(2x - \dfrac{\pi}{3}\right)~\) which compresses the graph horizontally by a factor of 2, including the horizontal shift. This reduces the horizontal shift from \(\dfrac{\pi}{3}\) to \(\dfrac{\pi}{6}\text{.}\) (See figure (b.)
It is easier to analyze the transformations in the function \(f\text{,}\) because we can read the horizontal shift from the formula.
\begin{equation*}
f(x) = \sin \left[2\left(x - \dfrac{\pi}{3}\right)\right]
\end{equation*}
where \(2\) is the compression factor and \(\dfrac{\pi}{3}\) is the horizontal shift.
We can write the formula for \(g(x)\) in the same easy-to-analyze form by factoring the input for the sine function:
\begin{equation*}
g(x) = \sin \left(2x - \dfrac{\pi}{3}\right) = \sin \left[2\left(x - \dfrac{\pi}{6}\right)\right]
\end{equation*}
In general, if we write the formula for a sinusoidal function in standard form, we can read all the transformations from the constants in the formula.
Standard Form for Sinusoidal Functions.
The graphs of the functions
\begin{equation*}
\blert{y = A\sin (B(x-h)) + k}~~~~ \text {and}~~~~ \blert{y = A\cos (B(x-h)) + k}
\end{equation*}
are transformations of the sine and cosine graphs.
The amplitude is \(\abs{A}\text{.}\)
The midline is \(y = k\text{.}\)
The period is \(\dfrac{2\pi}{\abs{B}},~~B \not= 0\text{.}\)
The horizontal shift is \(h\) units to the right if \(h\) is positive, and \(h\) units to the left if \(h\) is negative.
Example 7.19.
State the midline, amplitude, period, and horizontal shift for the function
\begin{equation*}
f(x) = 4\cos (3x+\pi) - 2
\end{equation*}
Sketch a graph of the function for \(-\pi \le x \le \pi\text{.}\)
Solution.
First, we write the input for the cosine function in factored form:
\begin{equation*}
f(x) = 4\cos \left[3\left(x+\dfrac{\pi}{3}\right)\right] - 2
\end{equation*}
Comparing the formula for \(f\) with the standard form, we see that \(A=4\text{,}\) \(B=3,~h = \dfrac{-\pi}{3}\text{,}\) and \(k = 2\text{.}\) Thus, the midline is \(y = -2\text{,}\) the amplitude is \(4\text{,}\) the period is \(\dfrac{2\pi}{3}\text{,}\) and the horizontal shift is \(\dfrac{\pi}{3}\) units to the left.
-
Use a table of values to locate the guidepoints for the graph. Begin by choosing convenient values for the input, \(3x+\pi\text{.}\) Then work backwards to find values for \(x\) and forwards to find values for \(f(x)\text{.}\)
| \(x\) |
\(3x\) |
\(3x+\pi\) |
\(\cos(3x+\pi) \) |
\(4\cos \left(3(x+\dfrac{\pi}{3})\right)-2\) |
| \(\dfrac{-\pi}{3}\) |
\(-\pi\) |
\(0\) |
\(1\) |
\(2\) |
| \(\dfrac{-\pi}{6}\) |
\(\dfrac{-\pi}{2}\) |
\(\dfrac{\pi}{2}\) |
\(0\) |
\(-2\) |
| \(0\) |
\(0\) |
\(\pi\) |
\(-1\) |
\(-6\) |
| \(\dfrac{\pi}{6}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{3\pi}{2}\) |
\(0\) |
\(-2\) |
| \(\dfrac{\pi}{3}\) |
\(\pi\) |
\(2\pi\) |
\(1\) |
\(2\) |
Finally, plot the guidepoints and connect them with a sinusoidal curve. The graph is shown below.
Checkpoint 7.20.
State the midline, amplitude, period, and horizontal shift of the graph of
\begin{equation*}
g(x) = 150 - 25\cos \left(4x-\dfrac{\pi}{2}\right)
\end{equation*}
-
Make a table of values and sketch a graph of the function.
| \(x\) |
\(4x\) |
\(4x-\dfrac{\pi}{2}\) |
\(\cos\left(4x-\dfrac{\pi}{2}\right) \) |
\(150 - 25\cos\left(4x-\dfrac{\pi}{2}\right)\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
Answer.
midline: \(y=150\text{,}\) amplitude: \(25\text{,}\) period: \(\dfrac{\pi}{2}\text{,}\) horizontal shift: \(\dfrac{\pi}{8}\) to the right
-
| \(x\) |
\(4x\) |
\(4x-\dfrac{\pi}{2}\) |
\(\cos\left(4x-\dfrac{\pi}{2}\right)\) |
\(150-25\cos\left(4x-\dfrac{\pi}{2}\right)\) |
| \(\dfrac{\pi}{8}\) |
\(\dfrac{\pi}{2}\) |
\(0\) |
\(1\) |
\(125\) |
| \(\dfrac{\pi}{4}\) |
\(\pi\) |
\(\dfrac{\pi}{2}\) |
\(0\) |
\(150\) |
| \(\dfrac{3\pi}{8}\) |
\(\dfrac{3\pi}{2}\) |
\(\pi\) |
\(-1\) |
\(175\) |
| \(\dfrac{\pi}{2}\) |
\(2\pi\) |
\(\dfrac{3\pi}{2}\) |
\(0\) |
\(150\) |
| \(\dfrac{5\pi}{8}\) |
\(\dfrac{5\pi}{2}\) |
\(2\pi\) |
\(1\) |
\(125\) |
Subsection Modeling with Sinusoidal Functions
In Section 7.1 we found formulas for sinusoidal functions that start on the midline, or at their maximum or minimum value. We can use horizontal transformations to write formulas for functions that start at other points on the cycle.
Example 7.21.
Find a formula for the sinusoidal function whose graph is shown below.
Solution.
The midline of the graph is \(y=0\text{,}\) and its amplitude is \(4\text{.}\) It has the shape of a cosine, but its maximum value occurs at \(x=\dfrac{\pi}{6}\) instead of at \(x=0\text{;}\) so the graph is shifted \(\dfrac{\pi}{6}\) units to the right, compared to the graph of \(y=\cos (x)\text{.}\)
The graph completes one cycle between \(x=\dfrac{\pi}{6}\) and \(x=\dfrac{13\pi}{6}\text{,}\) so its period is \(2\pi\text{.}\) Thus, we use the standard form \(y = A\cos B(x-h) + k\) with \(A=4,~B=1,~h=\dfrac{\pi}{6}\text{,}\) and \(k=0\text{,}\) giving us
\begin{equation*}
y = 4\cos \left(x-\dfrac{\pi}{6}\right)
\end{equation*}
as our formula for the function.
Checkpoint 7.23.
Find a formula for the sinusoidal function whose graph is shown at right.
Answer.
\(y = 6\sin \left(x - \dfrac{\pi}{4}\right)\)
Many natural phenomena can be modeled with sinusoidal functions.
Example 7.24.
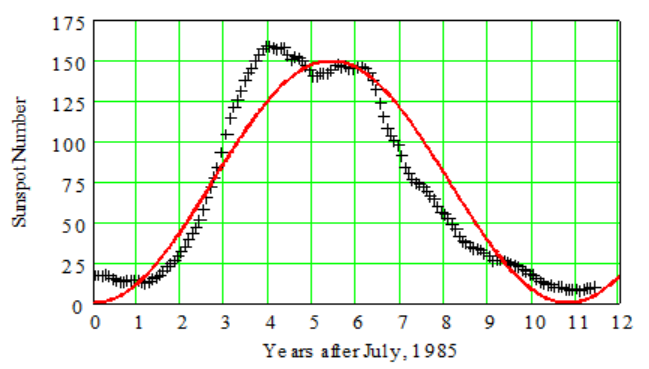
Sunspots are dark regions on the Sun first observed by Galileo in 1610. The number of sunspots is not constant, but varies with a period of approximately 11 years, called the solar cycle. Solar activity is directly related to this cycle, and can cause disturbances in the earth’s upper atmosphere. Planning for satellite orbits and space missions requires knowledge of solar activity levels years in advance.
The figure below shows sunspot data for the last solar cycle, from July, 1985 through June, 1996, and a sinusoidal function that models the data.
The period of the solar cycle shown is actually 10.8 years. Use this information and the graph to write a formula for the model.
Improve the fit of the model by adjusting its horizontal shift.
Solution.
The graph has the shape of
\(y=-\cos x\text{.}\) It appears to have midline
\(y=75\) and amplitude
\(75\text{,}\) so
\(k=75\) and
\(A=-75\) To find
\(B\text{,}\) we compute
\begin{equation*}
B=\dfrac{2\pi}{\text{period}}=\dfrac{2\pi}{10.8}=0.58
\end{equation*}
Thus, a formula for the model is
\(~y = 75-75\cos[0.58(x-h)]\text{.}\)
-
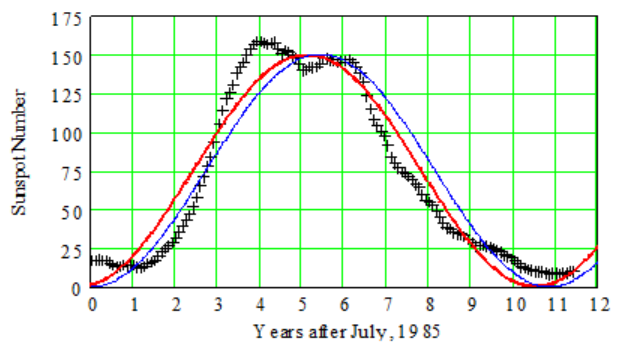
Fitting a curve by eye is a subjective process, but it looks like we can get a better fit by shifting the curve slightly to the left. By trying several values for \(h\) in
\begin{equation*}
y = 75-75\cos[0.58(x-h)]\text{,}
\end{equation*}
we might settle on \(h=0.3\text{,}\) which results in the curve shown below.
Checkpoint 7.25.
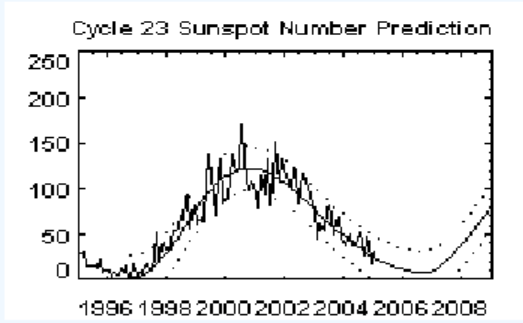
The figure below shows the sunspot data for the solar cycle that began in July 1996, and a curve of best fit calculated by NASA. This curve is not sinusoidal, but has a similar shape.
The minimum sunspot number occurred in October 1996. Use the graph to estimate the period, midline, and amplitude of a sinusoidal function that approximates the data.
Write a function that approximates the data.
Use your function to predict the sunspot number in January, 2005.
Answer.
Period: 10 years, midline: \(y=61.5\text{,}\) amplitude: 53
\(\displaystyle y=61.5-53\cos (x-0.25)\)
37
Review the following skills you will need for this section.
Algebra Refresher 7.26.
Write a formula for \(g(x)\text{.}\)
Graph \(f(x)\) and \(g(x)\) on the same axes.
\(\displaystyle f(x)=x^2,~g(x)=f(x-2)\)
\(\displaystyle f(x)=\sqrt{x},~g(x)=f(x+4)\)
\(\displaystyle f(x)=\dfrac{1}{x},~g(x)=f(x+1)\)
\(\displaystyle f(x)=\dfrac{1}{x^2},~g(x)=f(x-1)\)
\(\displaystyle f(x)=\abs{x},~g(x)=f(x-3)\)
\(\displaystyle f(x)=2^x,~g(x)=f(x+3)\)
\(\underline{\qquad\qquad\qquad\qquad}\)
Algebra Refresher Answers
-
\(\displaystyle g(x)=(x-2)^2\)
-
\(\displaystyle g(x)=\sqrt{x+4}\)
-
\(\displaystyle g(x)=\dfrac{1}{x+1}\)
-
\(\displaystyle g(x)=\dfrac{1}{(x-1)^2}\)
-
\(\displaystyle g(x)=\abs{x-3}\)
-
\(\displaystyle g(x)=2^{x+3}\)
Exercises Homework 7-2
1.
\(f(x)=\sin (x)~\) and \(~g(x)=\sin \left(x-\dfrac{\pi}{3}\right)\)
-
Fill in the table of values.
| \(x\) |
\(-\pi\) |
\(\dfrac{-5\pi}{6}\) |
\(\dfrac{-2\pi}{3}\) |
\(\dfrac{-\pi}{2}\) |
\(\dfrac{-\pi}{3}\) |
\(\dfrac{-\pi}{6}\) |
\(0\) |
\(\dfrac{\pi}{6}\) |
\(\dfrac{\pi}{3}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{2\pi}{3}\) |
\(\dfrac{5\pi}{6}\) |
\(\pi\) |
| \(f(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(g(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graphs of \(f\) and \(g\) on the same axes.
What is the horizontal shift from \(f\) to \(g\text{?}\)
Find all values of \(x\) for which \(\sin \left(x-\dfrac{\pi}{3}\right)=1\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
Find all values of \(x\) for which \(\sin \left(x-\dfrac{\pi}{3}\right)=0\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
2.
\(f(x)=\cos (x)~\) and \(~g(x)=\cos \left(x+\dfrac{\pi}{3}\right)\)
-
Fill in the table of values.
| \(x\) |
\(-\pi\) |
\(\dfrac{-5\pi}{6}\) |
\(\dfrac{-2\pi}{3}\) |
\(\dfrac{-\pi}{2}\) |
\(\dfrac{-\pi}{3}\) |
\(\dfrac{-\pi}{6}\) |
\(0\) |
\(\dfrac{\pi}{6}\) |
\(\dfrac{\pi}{3}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{2\pi}{3}\) |
\(\dfrac{5\pi}{6}\) |
\(\pi\) |
| \(f(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(g(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graphs of \(f\) and \(g\) on the same axes.
What is the horizontal shift from \(f\) to \(g\text{?}\)
Find all values of \(x\) for which \(\cos \left(x+\dfrac{\pi}{3}\right)=1\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
Find all values of \(x\) for which \(\cos \left(x+\dfrac{\pi}{3}\right)=0\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
3.
\(f(x)=\tan (x)~\) and \(~g(x)=\tan \left(x+\dfrac{\pi}{4}\right)\)
-
Fill in the table of values.
| \(x\) |
\(-\pi\) |
\(\dfrac{-3\pi}{4}\) |
\(\dfrac{-\pi}{2}\) |
\(\dfrac{-\pi}{4}\) |
\(0\) |
\(\dfrac{\pi}{4}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{3\pi}{4}\) |
\(\pi\) |
| \(f(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(g(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
Sketch the graphs of \(f\) and \(g\) on the same axes.
What is the horizontal shift from \(f\) to \(g\text{?}\)
Solve \(\tan \left(x+\dfrac{\pi}{4}\right)=1\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
Solve \(\tan \left(x+\dfrac{\pi}{4}\right)=0\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
4.
\(f(x)=\tan (x)~\) and \(~g(x)=\tan \left(x-\dfrac{\pi}{2}\right)\)
-
Fill in the table of values.
| \(x\) |
\(-\pi\) |
\(\dfrac{-3\pi}{4}\) |
\(\dfrac{-\pi}{2}\) |
\(\dfrac{-\pi}{4}\) |
\(0\) |
\(\dfrac{\pi}{4}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{3\pi}{4}\) |
\(\pi\) |
| \(f(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(g(x)\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
Sketch the graphs of \(f\) and \(g\) on the same axes.
What is the horizontal shift from \(f\) to \(g\text{?}\)
Solve \(\tan \left(x-\dfrac{\pi}{2}\right)=1\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
Solve \(\tan \left(x-\dfrac{\pi}{2}\right)=0\text{,}\) for \(-\pi \le x \le \pi\text{.}\)
5.
\(y = -2\cos\left(x+ \dfrac{\pi}{6}\right)\)
What are the amplitude and the horizontal shift?
-
Fill in the table of values.
| \(x\) |
\(x+\dfrac{\pi}{6}\) |
\(\cos\left(x+\dfrac{\pi}{6}\right) \) |
\(-2\cos\left(x+\dfrac{\pi}{6}\right)\) |
| \(\hphantom{0000}\) |
\(-\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{-\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(-2\cos\left(x+\dfrac{\pi}{6}\right)=1\text{,}\) for \(0 \le x \le 2\pi\)
Solve \(-2\cos\left(x+\dfrac{\pi}{6}\right)=0\text{,}\) for \(0 \le x \le 2\pi\)
6.
\(y = -6\sin\left(x- \dfrac{2\pi}{3}\right)\)
What are the amplitude and the horizontal shift?
-
Fill in the table of values.
| \(x\) |
\(x-\dfrac{2\pi}{3}\) |
\(\sin\left(x-\dfrac{2\pi}{3}\right) \) |
\(-6\sin\left(x-\dfrac{2\pi}{3}\right)\) |
| \(\hphantom{0000}\) |
\(-\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{-\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(-6\sin\left(x-\dfrac{2\pi}{3}\right)=3\text{,}\) for \(0 \le x \le 2\pi\)
Solve \(-6\sin\left(x-\dfrac{2\pi}{3}\right)=0\text{,}\) for \(0 \le x \le 2\pi\)
7.
The figure shows the graph of \(y = f(x)\text{.}\)
Find a formula for \(f(x)\) as a shift of the sine function.
Find a formula for \(f(x)\) as a shift of the cosine function.
8.
The figure shows the graph of \(y = f(x)\text{.}\)
Find a formula for \(f(x)\) as a shift of the sine function.
Find a formula for \(f(x)\) as a shift of the cosine function.
9.
The figure shows the graph of \(y = f(x)\text{.}\)
Find a formula for \(f(x)\) as a shift of the tangent function.
Find another formula for \(f(x)\) as a different shift of the tangent function.
10.
The figure shows the graph of \(y = f(x)\text{.}\)
Find a formula for \(f(x)\) as a shift of the tangent function.
Find another formula for \(f(x)\) as a different shift of the tangent function.
11.
\(y = \cos\left(2x-\dfrac{\pi}{3}\right)\)
What are the period and the horizontal shift? (Hint: Factor out 2 from \(2x-\dfrac{\pi}{3}\text{.}\))
-
Fill in the table of values.
| \(x\) |
\(2x\) |
\(2x-\dfrac{\pi}{3} \) |
\(\cos\left(2x-\dfrac{\pi}{3}\right)\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(\cos\left(2x-\dfrac{\pi}{3}\right)=1\text{,}\) for \(0 \le x \le 2\pi\)
Solve \(\cos\left(2x-\dfrac{\pi}{3}\right)=0\text{,}\) for \(0 \le x \le 2\pi\)
12.
\(y = \sin\left(3x+\dfrac{\pi}{2}\right)\)
What are the period and the horizontal shift? (Hint: Factor out 3 from \(3x+\dfrac{\pi}{2}\text{.}\))
-
Fill in the table of values.
| \(x\) |
\(3x\) |
\(3x+\dfrac{\pi}{2} \) |
\(\sin\left(3x+\dfrac{\pi}{2}\right)\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(\sin\left(3x+\dfrac{\pi}{2}\right)=1\text{,}\) for \(0 \le x \le 2\pi\)
Solve \(\sin\left(3x+\dfrac{\pi}{2}\right)=0\text{,}\) for \(0 \le x \le 2\pi\)
13.
\(y = \sin\left(\pi x+\dfrac{\pi}{3}\right)\)
What are the period and the horizontal shift? (Hint: Factor out \(\pi\) from \(\pi x+\dfrac{\pi}{3}\text{.}\))
-
Fill in the table of values.
| \(x\) |
\(\pi x\) |
\(\pi x+\dfrac{\pi}{3} \) |
\(\sin\left(\pi x+\dfrac{\pi}{3}\right)\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(\sin\left(\pi x+\dfrac{\pi}{3}\right)=1\text{,}\) for \(-2 \le x \le 2\)
Solve \(\sin\left(\pi x+\dfrac{\pi}{3}\right)=0\text{,}\) for \(-2 \le x \le 2\)
14.
\(y = \cos\left(\pi x-\dfrac{\pi}{3}\right)\)
What are the period and the horizontal shift? (Hint: Factor out \(\pi\) from \(\pi x-\dfrac{\pi}{3}\text{.}\))
-
Fill in the table of values.
| \(x\) |
\(\pi x\) |
\(\pi x-\dfrac{\pi}{3} \) |
\(\cos\left(\pi x-\dfrac{\pi}{3}\right)\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve \(\cos\left(\pi x-\dfrac{\pi}{3}\right)=1\text{,}\) for \(-2 \le x \le 2\)
Solve \(\cos\left(\pi x-\dfrac{\pi}{3}\right)=0\text{,}\) for \(-2 \le x \le 2\)
15.
\(y = 3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4\)
What are the midline, period, horizontal shift, and amplitude?
-
Fill in the table of values.
| \(x\) |
\(\dfrac{x}{2}\) |
\(\dfrac{x}{2}-\dfrac{\pi}{6} \) |
\(\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)\) |
\(3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve for
\(0 \le x \le 2\pi\text{:}\)
\begin{equation*}
3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4=1
\end{equation*}
Solve for
\(0 \le x \le 2\pi\text{:}\)
\begin{equation*}
3\sin\left(\dfrac{x}{2}-\dfrac{\pi}{6}\right)+4=4
\end{equation*}
16.
\(y = 2\cos\left(\dfrac{x}{3}-\dfrac{\pi}{4}\right)-1\)
What are the midline, period, horizontal shift, and amplitude?
-
Fill in the table of values.
| \(x\) |
\(\dfrac{x}{3}\) |
\(\dfrac{x}{3}-\dfrac{\pi}{4} \) |
\(\cos\left(\dfrac{x}{3}-\dfrac{\pi}{4}\right)\) |
\(2\cos\left(\dfrac{x}{3}-\dfrac{\pi}{4}\right)-1\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(0\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(\dfrac{3\pi}{2}\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
| \(\hphantom{0000}\) |
\(\hphantom{0000}\) |
\(2\pi\) |
\(\hphantom{0000}\) |
\(\hphantom{0000}\) |
-
Sketch the graph.
Solve for
\(0 \le x \le 6\pi\text{:}\)
\begin{equation*}
2\cos\left(\dfrac{x}{3}-\dfrac{\pi}{4}\right)-1=1
\end{equation*}
Solve for
\(0 \le x \le 6\pi\text{:}\)
\begin{equation*}
2\cos\left(\dfrac{x}{3}-\dfrac{\pi}{4}\right)-1=-1
\end{equation*}
17.
Find a formula for a sinusoidal function that has an amplitude of 2, a period of 3, and is shifted 4 units to the left and 5 units upwards compared with the sine function. Sketch the graph for \(0 \le x \le 3\text{.}\)
18.
Find a formula for a sinusoidal function that has an amplitude of 3, a period of 24, and is shifted 2 units to the right and 4 units upwards compared with the cosine function. Sketch the graph for \(0 \le x \le 24\text{.}\)
19.
Find a formula for a sinusoidal function that has an amplitude of 5, a period of 360, its midline at \(y=12\text{,}\) and passes through \((0,7)\text{.}\) Sketch the graph for \(0 \le x \le 360\text{.}\)
20.
Find a formula for a sinusoidal function that has an amplitude of 50, a period of 30, its midline at \(y=50\text{,}\) and passes through \((0,100)\text{.}\) Sketch the graph for \(0 \le x \le 30\text{.}\)
Exercise Group.
For Problems 21–26, find a formula for the circular function whose graph is shown.
Write the function in the form \(f(x)=A\sin (B(x-h))\text{.}\)
Write the function in the form \(f(x)=A\cos (B(x-h))\)
27.
The average daily high temperature in Fairbanks, Alaska can be approximated by a sinusoidal function with a period of 12 months. The low temperature of \(-1.6\degree\) occurs in January, and the high temperature of \(72.3\degree\) in July.
What are the midline, period, and amplitude?
Write a formula for the average daily high temperature \(T(m)\text{,}\) where \(m\) is the number of months since January.
Graph \(T(m)\) for two periods, labeling the points that correspond to highest and lowest average temperature.
28.
Depending on its phase, the moon looks like a disk that is partially visible and partially in shadow. The visible fraction ranges from 0% to 100%, and can be approximated by a sinusoidal function \(V(t)\text{,}\) where \(t\) is the number of days since the last full moon. The time between successive full moons (a lunar month) is 29.5 days.
What are the period, midline, and amplitude of \(V(t)\text{?}\)
Write a formula for \(V(t)\text{.}\)
Graph your function over two periods, labeling the points that correspond to full moon, half moon, and new moon.
29.
The tide in Yorktown is approximated by the function
\begin{equation*}
h(t)=1.4-1.4\cos(0.51t)
\end{equation*}
measured in feet above low tide, where \(t\) is the number of hours since the last low tide.
What are the midline, period, and amplitude?
Graph \(h(t)\) for two periods, labeling the points that correspond to high tide and low tide.
If the last low tide occurred at 5:00 am, predict when the next high and low tides will occur.
30.
The height of a child’s toy suspended at the end of a spring is approximated by a sinusoidal function. The toy’s height ranges between 200 centimeters and 260 centimeters above the ground, and it completes one up-and-down cycle every 0.8 second.
What are the midline, period, and amplitude?
Let \(h(t)\) be the height of the toy in centimeters, where \(t=0\) seconds corresponds to a time when the object was at the midline and moving upwards. Graph \(h(t)\) for two periods, labeling the points that correspond to the high and low positions of the toy.
When does the toy reach its maximum height the second time?
Exercise Group.
In Problems 31–34,
Estimate the amplitude, period, and midline of a circular function that fits the data.
Write a formula for the function.
31.
| \(t\) |
\(0\) |
\(0.25\) |
\(0.5\) |
\(0.75\) |
\(1\) |
\(1.25\) |
\(1.5\) |
\(1.75\) |
\(2\) |
\(2.25\) |
\(2.5\) |
| \(f(t)\) |
\(5.2\) |
\(4.26\) |
\(2\) |
\(-0.26\) |
\(-1.2\) |
\(-0.26\) |
\(2\) |
\(4.26\) |
\(5.2\) |
\(4.26\) |
\(2\) |
32.
| \(s\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
\(10\) |
| \(g(s)\) |
\(3\) |
\(2.58\) |
\(2.4\) |
\(2.58\) |
\(3\) |
\(3.42\) |
\(3.6\) |
\(3.42\) |
\(3\) |
\(2.58\) |
\(2.4\) |
33.
| \(x\) |
\(0\) |
\(0.1\) |
\(0.2\) |
\(0.3\) |
\(0.4\) |
\(0.5\) |
\(0.6\) |
\(0.7\) |
\(0.8\) |
| \(H(x)\) |
\(5\) |
\(7.9\) |
\(9.8\) |
\(9.8\) |
\(7.9\) |
\(5\) |
\(2.1\) |
\(0.2\) |
\(0.2\) |
34.
| \(t\) |
\(0\) |
\(0.79\) |
\(1.57\) |
\(2.36\) |
\(3.14\) |
\(3.93\) |
\(4.71\) |
\(5.50\) |
\(6.28\) |
| \(V(t)\) |
\(1\) |
\(-0.17\) |
\(-3\) |
\(-5.8\) |
\(-7\) |
\(-5.3\) |
\(-3\) |
\(-0.17\) |
\(1\) |