Alg-tool Equations of Lines

Section 1.5 Equations of Lines

Subsection 1. Calculate slope using a formula

Recall that the subscripts on the coordinates in $~P_1(x_1,y_1)~$ and $~P_2(x_2,y_2)~$ just mean "first point" and "second point".

Two-Point Formula for Slope.

The slope of the line joining points $~P_1(x_1,y_1)~$ and $~P_2(x_2,y_2)~$ is

\begin{equation*} m = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2-y_1}{x_2-x_1}~~~~~~\text{if}~~~~x_2 \not= x_1 \end{equation*}

Subsubsection Example

Example 1.70.

Compute the slope of the line joining $(-6,2)$ and $(3,-1)\text{.}$

Solution

It doesn't matter which point is $P_1$ and which is $P_2\text{,}$ so we choose $P_1$ to be $(-6,2)\text{.}$ Then $(x_1,y_1)=(-6,2)$ and $(x_2,y_2)=(3,-1)\text{.}$ Thus,

\begin{align*} m \amp = \dfrac{y_2-y_1}{x_2-x_1}\\ \amp = \dfrac{-1-2}{3-(-6)} = \dfrac{-3}{9} = \dfrac{-1}{3} \end{align*}

Caution 1.71.

Make sure that you subtract both the $x$ and $y$ coordinates in the same order! That is, do NOT calculate

\begin{equation*} \dfrac{y_{\alert{2}}-y_{\alert{1}}}{x_{\alert{1}}-x_{\alert{2}}}~~~~~~~~~~\blert{\text{Incorrect!}} \end{equation*}

or your slope will have the wrong sign.

Subsubsection Exercises

Checkpoint 1.72.

Compute the slope of the line joining the points $(5,2)$ and $(8,7)\text{.}$

Answer

$\dfrac{5}{3}$

Checkpoint 1.73.

Compute the slope of the line joining the points $(-3,-4)$ and $(-7,1)\text{.}$

Answer

$\dfrac{-5}{4}$

Subsection 2. Slope-Intercept Form

Because the $y$-intercept $(0,b)$ is the "starting value" of a linear model, and its rate of change is measured by its slope,$m\text{,}$ the equation for a linear model

\begin{equation*} y = \text{starting value} + \text{rate} \times x \end{equation*}

can be expressed in symbols as

\begin{equation*} y = b + mx \end{equation*}

Slope-Intercept Form.

If we write the equation of a linear function in the form,

\begin{equation*} f (x) = b + mx \end{equation*}

then $m$ is the slope of the line, and $b$ is the $y$-intercept.

Subsubsection Examples

Example 1.74.

The temperature inside a pottery drying oven starts at 70 degrees and is rising at a rate of 0.5 degrees per minute. Write a function for the temperature, $H\text{,}$ inside the oven after $t$ minutes.

Solution

At $t=0\text{,}$ the temperature is 70 degrees, so $b=70\text{.}$

The slope is given by the rate of increase of $H\text{,}$ so $m=0.5\text{.}$

Thus, the function is

\begin{equation*} H=70+0.5t \end{equation*}

Example 1.75.

A perfect score on a driving test is 120 points, and you lose 4 points for each wrong answer. Write a function for your score, $S\text{,}$ if you give $n$ wrong answers.

Solution

If $n=0\text{,}$ your score is 120, so $b=120\text{.}$

Your score decreases by 4 points per wrong answer, so $m=\dfrac{\Delta S}{\Delta n} = 4\text{.}$

The function is

\begin{equation*} S=120-4n \end{equation*}

Subsubsection Exercises

Checkpoint 1.76.

Monica has saved $7800 to live on while she attends college. She spends $600 a month. Write a function for the amount, $S\text{,}$ in Monica's savings account after $t$ months.

Answer

$b=7800~~$ and $~~m=-400~~\text{,}$ so $~~S=7800-600t$

Checkpoint 1.77.

Jesse opened a new doughnut shop in an old store-front. He invested $2400 in remodeling and set-up, and he makes about $400 per week from the business. Write a function giving the shop's financial standing, $F\text{,}$ after $w$ weeks.

Answer

$b=-2400~~$ and $~~m=400~~\text{,}$ so $~~F=-2400+400w$

Subsection 3. Point-Slope Form

If we don't know the $y$-intercept of a line but we do know one other point and the slope, we can still find an equation for the line.

Point-Slope Formula.

To find an equation for the line of slope $m$ passing through the point $(x_1,y_1)\text{,}$ use the point-slope formula

\begin{equation*} \dfrac{y-y_1}{x-x_1} = m \end{equation*}

\begin{equation*} y-y_1=m(x-x_1) \end{equation*}

Subsubsection Example

Example 1.78.

Find an equation for the line that passes through $(1,3)$ and has slope $-2\text{.}$

Solution

We substitute $x_1=\alert{1}\text{,}$ $y_1=\alert{3}\text{,}$ and $m=\alert{-2}$ into the point-slope formula.

\begin{align*} y-\alert{3} \amp = \alert{-2} (x-\alert{1}) \amp \amp \blert{\text{Apply the distributive law.}}\\ y-3 \amp = -2x + 2 \amp \amp \blert{\text{Add 3 to both sides.}}\\ y \amp = -2x + 5 \end{align*}

Example 1.79.

Find an equation for the line of slope $\dfrac{-1}{2}$ that passes through $(-3,-2)\text{.}$

Solution

We substitute $x_1=\alert{-3}\text{,}$ $y_1=\alert{-2}\text{,}$ and $m=\alert{\dfrac{-1}{2}}$ into the point-slope formula.

\begin{align*} \dfrac{y-(\alert{-2})}{x-(\alert{-3})} \amp = \alert{\dfrac{-1}{2}} \amp \amp \blert{\text{Simplify the left side.}}\\ \dfrac{y+2}{x+3} \amp = \dfrac{-1}{2} \amp \amp \blert{\text{Cross-multiply.}}\\ 2(y+2) \amp = -1(x+3) \amp \amp \blert{\text{Apply the distributive law.}}\\ 2y+4 \amp = -x-3 \amp \amp \blert{\text{Subtract 4 from both sides.}}\\ 2y \amp = -x-7 \amp \amp \blert{\text{Divide both sides by 2.}}\\ y \amp = \dfrac{-1}{2}x-\dfrac{7}{2} \end{align*}

Subsubsection Exercises

Checkpoint 1.80.

Find an equation for the line of slope $-4$ that passes through $(2,-5)\text{.}$

Answer

$y=-4x+3$

Checkpoint 1.81.

Find an equation for the line of slope $\dfrac{2}{3}$ that passes through $(-6,1)\text{.}$

Answer

$y=\dfrac{2}{3}x+5$

Subsection 4. Graphing a linear equation by the point-slope method

If we know one point on a line and its slope, we can sketch its graph without having to make a table of values.

Subsubsection Examples

Example 1.82.

Graph the line $~y=\dfrac{3}{4}x-2$

Solution

Step1: Begin by plotting the $y$-intercept, $(0,-2)\text{.}$

Step 2: We use the slope, $\dfrac{\Delta y}{\Delta x} = \dfrac{3}{4}\text{,}$ to find another point on the line, as follows. Start at the point $(0,-2)$ and move 3 units up and 4 units to the right. Plot a second point here, at $(4,1)\text{.}$

Step 3: Find a third point by writing the slope as $\dfrac{\Delta y}{\Delta x} = \dfrac{-3}{-4}\text{:}$ from $(0,-2)\text{,}$ move down 3 units and 4 units to the left. Plot a third point here, at $(-4,-5)\text{.}$

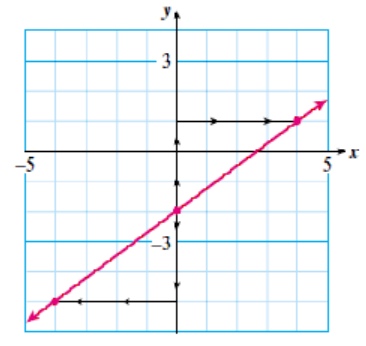
Finally, draw a line through the three points.

Example 1.83.

Graph the line of slope $\dfrac{-1}{2}$ that passes through $(-3,-2)\text{.}$

Solution

Step 1: Begin by plotting the point $(-3,-2)\text{.}$

Step 2: Use the slope, $\dfrac{\Delta y}{\Delta x} = \dfrac{-1}{2}\text{,}$ to find another point on the line, as follows. Start at the point $(-3,-2)$ and move 1 unit down and 2 units to the right. Plot a second point here, at $(-1,-3)\text{.}$

Step 3: Find a third point by writing the slope as $\dfrac{\Delta y}{\Delta x} = \dfrac{1}{-2}\text{:}$ from $(-3,-2)\text{,}$ move 1 unit up and 2 units to the left. Plot a third point here, at $(-5,-1)\text{.}$

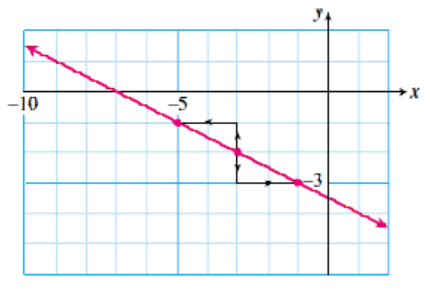
Finally, draw a line through the three points.

Subsubsection Exercises

Checkpoint 1.84.

Graph the line $~y=\dfrac{-1}{3}x-3$

Answer

Checkpoint 1.85.

Graph the line with slope $m=\dfrac{3}{2}$ passing through $(-1,-2)\text{.}$

Answer