Section 2.1 Linear Regression
Subsection 1. Read a scatterplot
We read the coordinates of points on a scatterplot the same way we do for any other graph.
Subsubsection Example
Example 2.1.
The scatterplot shows the height and shoe size of a group of men.
- State the height and shoe size of the man represented by point \(A\text{.}\)
- Find the heights of two men with the same shoe size.
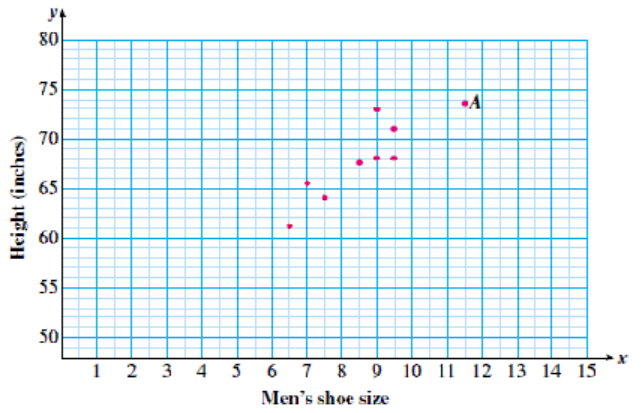
- The man represented by point \(A\) has shoe size \(11 \frac{1}{2}\) and is \(73 \frac{1}{2}\) inches tall.
- There are two men with shoe size 9, with heights 68 and 73 inches. There are also two men with shoe size \(9 \frac{1}{2}\text{,}\) with heights 68 and 71 inches.
Subsubsection Exercise
Checkpoint 2.2.
The scatterplot shows the heights of dance partners in a ballroom dance class.
- How tall is the shortest woman?
- What are the heights of the three partners of the 65-inch tall women?
- 59 in
- \(68 \frac{1}{2}\text{,}\) \(70\text{,}\) and \(71\) in
Subsection 2. Sketch a line of best fit
Of course, the points on a scatterplot may not lie on a straight line. But if they seem to cluster near a line, we can try to find that line.
Subsubsection Example
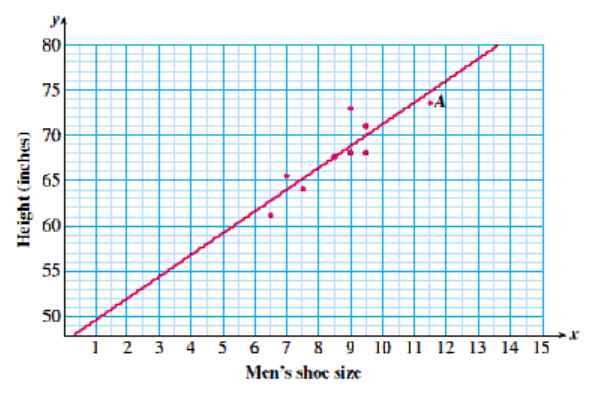
Example 2.3.
Sketch a line of best fit for the scatterplot in part 1.
We draw a line that lies as close as possible to all of the data points. As a rule of thumb, we try to keep equal numbers of points on each side of the line.
Subsubsection Exercise
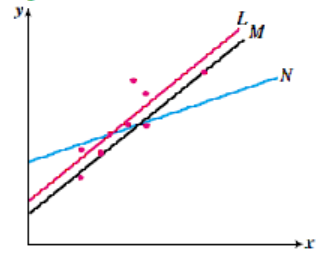
Checkpoint 2.4.
Which of the lines fits the scatterplot best?
Subsection 3. Fit a line through two points
If we don't know the slope of a line, but we do know two points on the line, we can calculate the slope first and then use the point-slope formula.
Subsubsection Example
Example 2.5.
Find an equation for the line that passes through \((2,-1)\) and \((-1,3)\text{.}\)
We solve this problem in two steps: First, find the slope of the line, and then use the point-slope formula.
Step 1: Let \((x_1,y_1)=(2,-1)\) and \((x_2,y_2)=(-1,3)\text{.}\) Use the slope formula to find
Step 2: Apply the point-slope formula with \(m=\dfrac{-4}{3}\) and \((x_1,y_1)=(2,-1)\text{.}\) (We can use either point in the formula.) Then
Cross-multiply to find
Subsubsection Exercise
Checkpoint 2.6.
Find an equation for the line that passes through \((-6,-1)\) and \((1,3)\text{.}\)
Step 1: Compute the slope.
Step 2: Use the point-slope formula.
