Alg-tool Slope

Section 1.4 Slope

Subsection 1. Use ratios for comparison

Slope is a type of ratio that compares vertical distance per unit of horizontal distance. We use ratios for comparison in other situations, for example, when shopping we might compute price per unit.

Subsubsection Examples

Example 1.58.

You are choosing between two brands of iced tea. Which is a better bargain: a 28-ounce bottle of Teatime for $1.82, or a 36-ounce bottle of Leafdream for $2.25?

Solution

Compute the ratio price per ounce for each brand.

\begin{equation*} \text{Teatime:}~~~\dfrac{182 \text{ cents}}{28 \text{ ounces}}= 6.5 \text{ cents per ounce} \end{equation*}

\begin{equation*} \text{Leafdream:}~~~\dfrac{225 \text{ cents}}{36 \text{ ounces}}= 6.25 \text{ cents per ounce} \end{equation*}

Leafdream is the better bargain.

Example 1.59.

The trail to Lookout Point gains 780 feet in elevation over a distance of 1.3 miles. The trail to Knife Edge gains 950 feet in elevation over a distance of 1.6 miles. Which trail is steeper?

Solution

Compute the ratio of elevation gain to horizontal distance traveled for each trail.

\begin{equation*} \text{Lookout Point:}~~~\dfrac{780 \text{ feet}}{1.3 \text{ miles}}= 600 \text{ feet per mile} \end{equation*}

\begin{equation*} \text{Knife Edge:}~~~\dfrac{950 \text{ feet}}{1.6 \text{ miles}}= 593.75 \text{ feet per mile} \end{equation*}

The Lookout Point trail is steeper.

Subsubsection Exercises

Checkpoint 1.60.

Rachel drove 292.4 miles on 8.6 gallons of gasoline. Reuben drove 390 miles on 12 gallons of gasoline. Who got the better gas mileage?

Hint: Compute the ratio miles per gallon.

Answer

Rachel: 34 miles per gallon; Reuben: 32.5 miles per gallon

Checkpoint 1.61.

Leslie drove 168 miles in 2.8 hours, and Mark drove 224 miles in 3.5 hours. Who drove at the greater average speed?

Hint: Compute the ratio miles per hour.

Answer

Mark: 64 miles per hour; Leslie: 60 miles per hour

Subsection 2. Calculate slope from a graph

We often think of slope as measuring the "steepness" of a graph, but the appearance of steepness is also affected by the scales on the axes.

Subsubsection Examples

Example 1.62.

Calculate the slope of the line.

Solution

Choose two points on the line, and calculate the ratio of vertical change to horizontal change. Use the grid lines on the graph, but don't forget to note the scales on the axes.

line marked with horizontal and vertical change between two points

The slope is the ratio $\dfrac{\Delta h}{\Delta t}\text{.}$ The variable on the horizontal axis increases by 4 units, from 2 to 6, so $\Delta t=4\text{.}$ The variable on the vertical axis increases by 8 grid lines, but each grid line represents 2 units, so $\Delta h=16\text{.}$ Thus, the slope is $\dfrac{\Delta h}{\Delta t} = \dfrac{16}{4}=4\text{.}$

Example 1.63.

Calculate the slope of the line.

Solution

Choose two points on the line, and calculate the ratio of vertical change to horizontal change. Use the grid lines on the graph, but don't forget to note the scales on the axes.

The slope is the ratio $\dfrac{\Delta V}{\Delta t}\text{.}$ The horizontal variable, $t\text{,}$ increases by 6 grid lines, but each grid line represents 2 units, so $\Delta t=12\text{.}$ The vertical variable, $V\text{,}$ decreases by 3 grid lines, or 6 units, so $\Delta V=-6\text{.}$ Thus, $\dfrac{\Delta V}{\Delta t} = \dfrac{-6}{12}=\dfrac{-1}{2}\text{.}$

Subsubsection Exercises

Checkpoint 1.64.

Calculate the slope of the line.

Hint: Find two points that lie on the intersection of grid lines, so that it's easy to read their coordinates. For example, you could use $(2, 300)$ and $(8, 600)\text{.}$

Answer

$50$

Checkpoint 1.65.

Calculate the slope of the line.

Hint: Find two points that lie on the intersection of grid lines. For example, you could use $(0, 60)$ and $(3, -12)\text{.}$

Answer

$-24$

Subsection 3. Calculate volume

The volume of a box is measured in cubic units and can be calculated using the formula $V=lwh\text{,}$ where $l,~w,$ and $h$ stand for the length, width, and height of the box. Volume measures the amount of space inside an object by telling us how many blocks 1 unit on a side will fit inside the space. For example, the volume of the box below, whose dimensions are given in centimeters, is

\begin{align*} V \amp = lwh \\ \amp = (6)(4)(3) = 72~ \text{cubic centimeters} \end{align*}

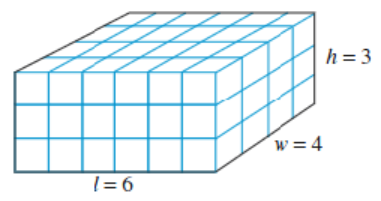
It may seem difficult to measure the inside of a round object like a sphere or a cone in cubic units, but you can imagine filling the object with liquid and then pouring the liquid into a box to measure its volume.

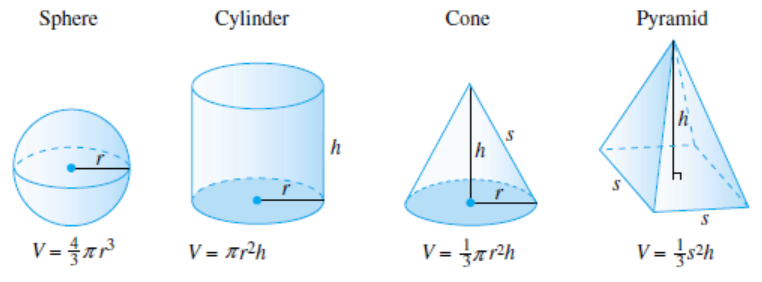
Subsubsection Examples

Example 1.66.

An aquarium is 24 inches long and 10 inches wide. What is the area of its base? How much water is needed to fill it to a depth of 5 inches?

Solution

The area of the base is

\begin{equation*} A=lw=(24~ \text{in})(10~ \text{in})=240~ \text{in}^2 \end{equation*}

To calculate the volume of water, we can multiply the area of the base, $lw\text{,}$ by the height of the water, $h\text{.}$

\begin{equation*} V=(lw)h=Ah=(240~ \text{in}^2)(5~ \text{in})=1200~ \text{in}^3 \end{equation*}

Example 1.67.

The diameter of a spherical wax candle is 5 inches. What is the volume of wax in the candle?

Solution

The radius of the candle is half its diameter, or 2.5 inches. The volume of the candle is

\begin{equation*} V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi(2.5~ \text{in})^3=65.45~\text{in}^3 \end{equation*}

Subsubsection Exercises

Checkpoint 1.68.

Find the volume of a cylindrical water tank whose diameter is 20 feet and whose height is 20 feet.

Answer

6283.2 cubic feet

Checkpoint 1.69.

The diameter of the Earth is about 7920 miles. Find its volume.

Answer

About 260,120,000,000 cubic miles