MFG Properties of Lines

Section A.12 Properties of Lines

Subsection Horizontal and Vertical Lines

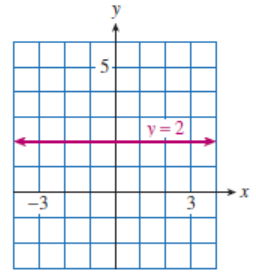
Two special cases of linear equations are worth noting. First, an equation such as $y=4$ can be thought of as an equation in two variables,

\begin{equation*} 0x+y=4 \end{equation*}

For each value of $x\text{,}$ this equation assigns the value $\alert{4}$ to $y\text{.}$ Thus, any ordered pair of the form $(x,4)$ is a solution of the equation. For example,

\begin{equation*} (-1,\alert{4}),~~(2,\alert{4})~~\text{and}~~(4,\alert{4}) \end{equation*}

are all solutions of the equation. If we draw a straight line through these points, we obtain the horizontal line shown at left below.

$horizontal line$

$vertical line$

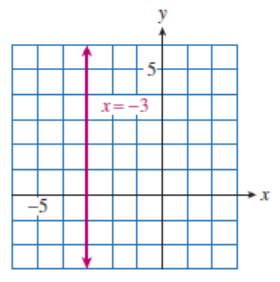
The other special case of a linear equation is of the type $x=3\text{,}$ or

\begin{equation*} x+0y=3 \end{equation*}

Here, only one value is permissible for $x\text{,}$ namely $\alert{3}\text{,}$ while any value may be assigned to $y\text{.}$ Any ordered pair of the form $(3,y)$ is a solution of this equation. If we choose two solutions, say $(\alert{3},1)$ and $(\alert{3},3)\text{,}$ and draw a straight line through these two points, we have the vertical line shown at right above. In general, we have the following results.

The graph of $~~x=k~~$ ($k$ a constant) is a vertical line.

The graph of $~~y=k~~$ ($k$ a constant) is a horizontal line.

Example A.108.

Graph $~y=2\text{.}$
Graph $~x=-3\text{.}$

Solution.

Now let’s compute the slopes of the two lines in the previous example. Choose two points on the graph of $y=2\text{,}$ say $(-5,2)$ and $(4,2)\text{.}$ Use these points to compute the slope.

\begin{equation*} m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{2-2}{4-(-5)}=\dfrac{0}{9}=0 \end{equation*}

The slope of the horizontal line $y=2$ is zero. In fact, the slope of any horizontal line is zero, because the $y$ -coordinates of all the points on the line are equal. Thus

\begin{equation*} m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{0}{x_2-x_1}=0 \end{equation*}

On a vertical line, the $x$-coordinates of all the points are equal. For example, two points on the line $x=-3$ are $(-3,1)$ and $(-3,6)\text{.}$ Using these points to compute the slope, we find

\begin{equation*} m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{6-1}{-3-(-3)}=\dfrac{5}{0} \end{equation*}

which is undefined. The slope of any vertical line is undefined because the expression $x_2-x_1$ equals zero.

The slope of a horizontal line is zero.

The slope of a vertical line is undefined.

Subsection Parallel and Perpendicular Lines

Consider the graphs of the equations

\begin{gather*} y=\dfrac{2}{3}x-4\\ y=\dfrac{2}{3}x+2 \end{gather*}

shown below.

$parallel lines$

The lines have the same slope, $\dfrac{2}{3}\text{,}$ but different $y$-intercepts. Because slope measures the steepness or inclination of a line, lines with the same slope are parallel.

Two lines with slopes $m_1$ and $m_2$ are parallel if and only if $m_1=m_2\text{.}$

Example A.109.

Are the graphs of the equations $3x+6y=6$ and $y=-\dfrac{1}{2}x+5$ parallel?

Solution.

The lines are parallel if their slopes are equal. We can find the slope of the first line by putting its equation into slope-intercept form. We solve for $y\text{:}$

\begin{equation*} \begin{aligned}[t] 3x+6y \amp = 6 \amp \amp \blert{\text{Subtract}~ 3x~ \text{from both sides.}}\\ 6y \amp = -3x + 6 \amp \amp \blert{\text{Divide both sides by}~6.}\\ y \amp = \dfrac{-3x}{6} + \dfrac{6}{6} \amp \amp \blert{\text{Simplify.}}\\ y = \amp = -\dfrac{1}{2}x + 1\\ \end{aligned} \end{equation*}

The slope of the first line is $m_1=-\dfrac{1}{2}\text{.}$ The equation of the second line is already in slope-intercept form, and its slope is $m_2=-\dfrac{1}{2}\text{.}$ Thus, $m_1=m_2\text{,}$ so the lines are parallel.

Now consider the graphs of the equations

\begin{gather*} y=\dfrac{2}{3}x-2\\ y=-\dfrac{3}{2}x+3 \end{gather*}

shown below.

$perpendicular lines$

The lines appear to be perpendicular. The relationship between the slopes of perpendicular lines is not as easy to see as the relationship for parallel lines. However, for this example, $m_1=\dfrac{2}{3}$ and $m_2=-\dfrac{3}{2}\text{.}$ Note that

\begin{equation*} m_2=-\dfrac{3}{2} = \dfrac{-1}{\dfrac{2}{3}} = \dfrac{-1}{m_1} \end{equation*}

This relationship holds for any two perpendicular lines with slopes $m_1$ and $m_2\text{,}$ as long as $m_1 \not= 0$ and $m_2 \not= 0\text{.}$

Two lines with slopes $m_1$ and $m_2$ are perpendicular if

\begin{equation*} m_2=\dfrac{-1}{m_1}\text{.} \end{equation*}

We say that $m_2$ is the negative reciprocal of $m_1\text{.}$

Example A.110.

Are the graphs of $3x-5y=5$ and $2y=\dfrac{10}{3}x+3$ perpendicular?

Solution.

We find the slope of each line by putting the equations into slope-intercept form. For the first line,

\begin{equation*} \begin{aligned}[t] 5y \amp = 3x-5 \amp \amp \blert{\text{Divide both sides by}~ 5.}\\ y \amp = \dfrac{3}{5}x - 1\\ \end{aligned} \end{equation*}

so $m_1=\dfrac{3}{5}\text{.}$ For the second line, $y=\dfrac{5}{3}x+\dfrac{3}{2}\text{,}$ so $m_2=\dfrac{5}{3}\text{.}$ Now, the negative reciprocal of $m_1$ is

\begin{equation*} \dfrac{-1}{m_1}=\dfrac{-1}{\dfrac{3}{5}}=\dfrac{-5}{3} \end{equation*}

but $m_2=\dfrac{5}{3}\text{.}$ Thus, $m_2 \not= \dfrac{-1}{m_1}\text{,}$ so the lines are not perpendicular.

Subsection Applications to Geometry

These relationships for the slopes of parallel and perpendicular lines can help us solve numerous geometric problems.

Example A.111.

Show that the triangle with vertices $A(0,8),~B(6,2),~$ and $C(-4,4)$ shown below is a right triangle.

$right triangle$

Solution.

We will show that two of the sides of the triangle are perpendicular. The line segment $\overline{AB}$ has slope

\begin{equation*} m_1 = \dfrac{2-8}{6-0} = \dfrac{-6}{6} = -1 \end{equation*}

and the line segment $\overline{AC}$ has slope

\begin{equation*} m_2 = \dfrac{4-8}{-4-0} = \dfrac{-4}{-4} = 1 \end{equation*}

Because

\begin{equation*} \dfrac{-1}{m_1} = \dfrac{-1}{-1} = 1 = m_2, \end{equation*}

the sides $\overline{AB}$ and $\overline{AC}$ are perpendicular, and the triangle is a right triangle.

Consider the graph of $4x-2y=6$ shown below.

$parallel lines$

Can we find the equation of the line that is parallel to this line, but passes through the point $(1,4)\text{?}$ If we can find the slope of the desired line, we can use the slope-intercept formula to find its equation.

Now because the line we want is parallel to the given line, they must have the same slope. To find the slope of the given line, we write its equation in slope-intercept form:

\begin{equation*} \begin{aligned}[t] 4x-2y \amp = 6 \amp \amp \blert{\text{Subtract}~4x~\text{from both sides.}}\\ -2y \amp = -4x+6 \amp \amp\ \blert{\text{Divide both sides by}~-2.}\\ y \amp = 2x-3\\ \end{aligned} \end{equation*}

The slope of the given line is $2\text{.}$ Because the unknown line is parallel to this line, its slope is also $2\text{.}$ Now we know the slope of the desired line, $m=2\text{,}$ and one point on the line, $(1,4)\text{.}$ Substituting these values into the point-slope formula will give us the equation.

\begin{equation*} \begin{aligned}[t] y-y_1 \amp = m(x-x_1)\\ y-\alert{4} \amp = \alert{2}(x-\alert{1}) \amp \amp \blert{\text{Apply the distributive law.}}\\ y-4\amp = 2x-2 \amp \amp \blert{\text{Add 4 to both sides.}}\\ y\amp = 2x+2 \end{aligned} \end{equation*}

Example A.112.

Find an equation for the line that passes through the point $(1,4)$ and is perpendicular to the line $4x-2y=6\text{.}$

Solution.

We follow the same strategy as in the discussion above: First find the slope of the desired line, then use the point-slope formula to write its equation.

The line we want is perpendicular to the given line, so its slope is the negative reciprocal of $m_1=2\text{,}$ the slope of the given line. Thus

\begin{equation*} m_2 = \dfrac{-1}{m_1} = \dfrac{-1}{2} \end{equation*}

Now we use the point-slope formula with $m_2= \dfrac{-1}{2}$ and $(x_1,y_1)=(1,4)\text{.}$

\begin{equation*} \begin{aligned}[t] y-y_1 \amp = m(x-x_1)\\ y-\alert{4} \amp = \alert{\dfrac{-1}{2}}(x-\alert{1}) \amp \amp \blert{\text{Apply the distributive law.}}\\ y-4\amp = \dfrac{-1}{2}x+\dfrac{1}{2} \amp \amp \blert{\text{Add 4 to both sides.}}\\ y\amp = \dfrac{-1}{2}x+\dfrac{9}{2} \amp \amp \blert{\dfrac{1}{2}+4 = \dfrac{1}{2}+\dfrac{8}{2}=\dfrac{9}{2}}\\ \end{aligned} \end{equation*}

The given line and the perpendicular line are shown below.

$perpendicular lines$

Subsection Section Summary

Subsubsection Vocabulary

Look up the definitions of new terms in the Glossary.

Horizontal
Vertical
Parallel
Perpendicular

Subsubsection SKILLS

Practice each skill in the exercises listed.

Sketch horizontal and vertical lines: #1–6
Find an equation for a horizontal or vertical line: #7–12
Identify parallel or perpendicular lines: #15–24
Find equations for parallel or perpendicular lines: #25–36

Subsubsection Reading Questions

Give an example of an equation for a vertical line, and for a horizontal line.
Why is the slope of a vertical line undefined?
What is the best way to determine whether two lines are parallel?
Suppose you know the equation of a certain line. Explain how to find the slope of a second line perpendicular to the first line.

Exercises Exercises A.12

Exercise Group.

For Problems 1–6,

Sketch a rough graph of each equation, and label its intercept.
State the slope of each line.

1.

$y=-3$

2.

$x=-2$

3.

$2x=8$

4.

$3y=15$

5.

$x=0$

6.

$y=0$

Exercise Group.

For Problems 7–12, find the equation of the line described.

7.

A vertical line through the point $(-5,8)$

8.

A horizontal line through the point $(2,-4)$

9.

The $x$-axis

10.

The $y$-axis

11.

Perpendicular to $x=3$ and intersecting it at $(3,9)$

12.

Parallel to the $y$-axis and including the point $(-1,-2)$

Exercise Group.

For Problems 13 and 14,

Determine whether the slope of each line is positive, negative, zero, or undefined.
List the lines in order of increasing slope.

13.

14.

15.

Use your calculator to graph the equations $y=3x+8$ and $y=3.1x+6$ together in the standard window. Do you think the lines are parallel?
Find the slope of each line in part (a). Are the lines parallel?
Find the $y$-value for each equation when $x=20\text{.}$ What do your answers tell you about the two lines?

16.

Use your calculator to graph the equation $y=0.001x+4$ in the standard window. Do you think the line is horizontal?
Find the slope and the $x$-intercept of the line in part (a). Is the line horizontal?
Graph the equation in part (a) in the window

$\text{Xmin}=-5000\text{; Xmax}=5000$

$\text{Ymin}=-10\text{; Ymax}=10 $

Find the coordinates of two convenient points on the line, and compute its slope using the slope formula.

17.

The slopes of several lines are given below. Which of the lines are parallel to the graph of $y=0.75x+2\text{,}$ and which are perpendicular to it?

$\displaystyle m=\dfrac{3}{4}$
$\displaystyle m=\dfrac{8}{6}$
$\displaystyle m=\dfrac{-20}{15}$
$\displaystyle m=\dfrac{-39}{52}$
$\displaystyle m=\dfrac{4}{3}$
$\displaystyle m=\dfrac{-16}{12}$
$\displaystyle m=\dfrac{36}{48}$
$\displaystyle m=\dfrac{9}{12}$

18.

The slopes of several lines are given below. Which of the lines are parallel to the graph of $y=2.5x-3\text{,}$ and which are perpendicular to it?

$\displaystyle m=\dfrac{2}{5}$
$\displaystyle m=\dfrac{25}{10}$
$\displaystyle m=\dfrac{-8}{20}$
$\displaystyle m=\dfrac{-45}{18}$
$\displaystyle m=\dfrac{40}{16}$
$\displaystyle m=25$
$\displaystyle m=\dfrac{-1}{25}$
$\displaystyle m=\dfrac{-5}{10}$

19.

In each part, determine whether the two lines are parallel, perpendicular, or neither.

$\displaystyle y=\dfrac{3}{5}x-7,~~3x-5y=2$
$\displaystyle y=4x+3,~~y=\dfrac{1}{4}x-3$
$\displaystyle 6x+2y=1,~~x=1-3y$
$\displaystyle 2y=5,~~5y=-2$

20.

In each part, determine whether the two lines are parallel, perpendicular, or neither.

$\displaystyle 2x-7y=14,~~7x-2y=14$
$\displaystyle x+y=6,~~x-y=6$
$\displaystyle x=-3,~~3y=5$
$\displaystyle \dfrac{1}{4}x-\dfrac{3}{4}y=\dfrac{2}{3},~~\dfrac{1}{6}x+\dfrac{1}{2}y=\dfrac{1}{3}$

21.

Sketch the triangle with vertices $A(2,5),~B(5,2),$ and $C(10,7)\text{.}$
Show that the triangle is a right triangle. (Hint: What should be true about the slopes of the two sides that form the right angle?)

22.

Sketch the triangle with vertices $P(-1,3),~Q(-3,8),$ and $R(4,5)\text{.}$
Show that the triangle is a right triangle. (See the hint for Problem 21.)

23.

Sketch the quadrilateral with vertices $P(2,4),~Q(3,8),~R(5,1),$ and $S(4,-3)\text{.}$
Show that the quadrilateral is a parallelogram. (Hint: What should be true about the slopes of the opposite sides of the parallelogram?)

24.

Sketch the quadrilateral with vertices $A(-5,4),~B(7,-11),~C(12,25),$ and $D(0,40)\text{.}$
Show that the quadrilateral is a parallelogram. (See the hint for Problem 23.)

25.

Show that the line passing through the points $A(0,-3)$ and $B(3,\dfrac{1}{2})$ also passes through the point $C(-6,-10)\text{.}$

26.

Do the points $P(-5,-3\dfrac{1}{2}),~Q(4,-2)$ and $R(9\dfrac{1}{2},-1)$ lie on the same line? Why or why not?

Exercise Group.

Use graph paper for Problems 27-30.

27.

Put the equation $x-2y=5$ into slope-intercept form, and graph the equation.
What is the slope of any line that is parallel to $x-2y=5\text{?}$
On your graph for part (a), sketch by hand a line that is parallel to $x-2y=5$ and passes through the point $(2,-1)\text{.}$
Use the point-slope formula to write an equation for the line that is parallel to the graph of $x-2y=5$ and passes through the point $(2,-1)\text{.}$

28.

Put the equation $2y-3x=5$ into slope-intercept form, and graph the equation.
What is the slope of any line that is parallel to $2y-3x=5\text{?}$
On your graph for part (a), sketch by hand a line that is parallel to $2y-3x=5$ and passes through the point $(-3,2)\text{.}$
Use the point-slope formula to write an equation for the line that is parallel to the graph of $2y-3x=5$ and passes through the point $(-3,2)\text{.}$

29.

Put the equation $2y-3x=5$ into slope-intercept form, and graph the equation.
What is the slope of any line that is perpendicular to $2y-3x=5\text{?}$
On your graph for part (a), sketch by hand a line that is perpendicular to $2y-3x=5$ and passes through the point $(1,4)\text{.}$
Use the point-slope formula to write an equation for the line that is perpendicular to the graph of $2y-3x=5$ and passes through the point $(1,4)\text{.}$

30.

Put the equation $x-2y=5$ into slope-intercept form, and graph the equation.
What is the slope of any line that is perpendicular to $x-2y=5\text{?}$
On your graph for part (a), sketch by hand a line that is perpendicular to $x-2y=5$ and passes through the point $(4,-3)\text{.}$
Use the point-slope formula to write an equation for the line that is perpendicular to the graph of $x-2y=5$ and passes through the point $(4,-3)\text{.}$

31.

Two of the vertices of rectangle $ABCD$ are $A(-5,2)$ and $B(-2,4)\text{.}$

Find an equation for the line that includes side $\overline{AB}\text{.}$
Find an equation for the line that includes side $\overline{BC}$ .

32.

Two of the vertices of rectangle $PQRS$ are $P(-2,-6)$ and $Q(4,-4)\text{.}$

Find an equation for the line that includes side $\overline{PQ}\text{.}$
Find an equation for the line that includes side $\overline{QR}\text{.}$

Exercise Group.

For Problems 33 and 33, recall from geometry that the altitude from one vertex of a triangle to the opposite side is perpendicular to that side.

33.

Sketch the triangle with vertices $A(-6,-3),~B(-6,3)$ and $C(4,5)\text{.}$
Find the slope of the side $\overline{AC}\text{.}$
Find the slope of the altitude from point $B$ to side $\overline{BC}\text{.}$
Find an equation for the line that includes the altitude from point $B$ to side $\overline{BC}\text{.}$

34.

Sketch the triangle with vertices $A(-5,12),~B(4,-2)$ and $C(1,-6)\text{.}$
Find the slope of the side $\overline{AC}\text{.}$
Find the slope of the altitude from point $B$ to side $\overline{BC}\text{.}$
Find an equation for the line that includes the altitude from point $B$ to side $\overline{BC}\text{.}$

Exercise Group.

For Problems 35 and 36, recall from geometry that the tangent line to a circle is perpendicular to the radius to the point of tangency.

35.

The center of a circle is the point $C(2,4)\text{,}$ and $P(-1,6)$ is a point on the circle, as shown below. Find the equation of the line tangent to the circle at the point $P\text{.}$

36.

The center of a circle is the point $D(-2,1)\text{,}$ and $Q(1,-3)$ is a point on the circle, as shown below. Find the equation of the line tangent to the circle at the point $Q\text{.}$

37.

In this exercise we will show that parallel lines have the same slope. In the figure below, $l_1$ and $l_2$ are two parallel lines that are neither horizontal nor vertical. Their $y$-intercepts are $A$ and $B\text{.}$ The segments $\overline{AC}$ and $\overline{CD}$ are constructed parallel to the $x$-and $y$-axes, respectively.

Explain why each of the following statements is true.

Angle $ACD$ equals angle $CAB\text{.}$
Angle $DAC$ equals angle $ACB\text{.}$
Triangle $ACD$ is similar to triangle $CAB\text{.}$
$\displaystyle m_1=\dfrac{CD}{AC};~~m_2=\dfrac{AB}{AC}$
$\displaystyle m_1=m_2$

38.

In this exercise we will show that if two lines with slopes $m_1$ and $m_2$ (where neither line is vertical) are perpendicular, then $m_2$ is the negative reciprocal of $m_1\text{.}$ In the figure below, lines $l_1$ and $l_2$ are perpendicular. Their $y$-intercepts are $B$ and $C\text{.}$ The segment $\overline{AP}$ is constructed through the point of intersection of $l_1$ and $l_2$ parallel to the $x$-axis.

Explain why each of the following statements is true.

Angles $ABC$ and $ACB$ are complementary.
Angles $ABC$ and $BAP$ are complementary.
Angle $BAP$ equals angle $ACB\text{.}$
Angles $CAP$ and $ACB$ are complementary.
Angle $CAP$ equals angle $ABC\text{.}$
Triangle $ABP$ is similar to triangle $CAP\text{.}$
$\displaystyle m_1=\dfrac{BP}{AP};~~m_2=-\dfrac{CP}{AP}$
$\displaystyle m_2=\dfrac{-1}{m_1}$

Prev Top Next