MFG Answers to Selected Exercises

Appendix G Answers to Selected Exercises

1 Functions and Their Graphs
1.1 Linear Models
Homework 1.1

1.

Answer.

$h$	$0$	$3$	$6$	$9$	$10$
$T$	$65$	$80$	$95$	$110$	$115$

$\displaystyle T=65+5h$
$\displaystyle 95\degree$
3 p.m.

3.

Answer.

$w$	$0$	$4$	$8$	$12$	$16$
$A$	$250$	$190$	$130$	$70$	$10$

$\displaystyle A=250-15w$
75 gallons
Until the fifth week

5.

Answer.

$\displaystyle P=-800+40t$
$(0,-800)\text{,}$ $(20,0)$
The $P$-intercept, $-800\text{,}$ is the initial $(t = 0)$ value of the profit. Phil and Ernie start out $\$800$ in debt. The $t$-intercept, $20\text{,}$ is the number of hours required for Phil and Ernie to break even.

7.

Answer.

$\displaystyle C=5000+0.125d$
Complete the table of values.

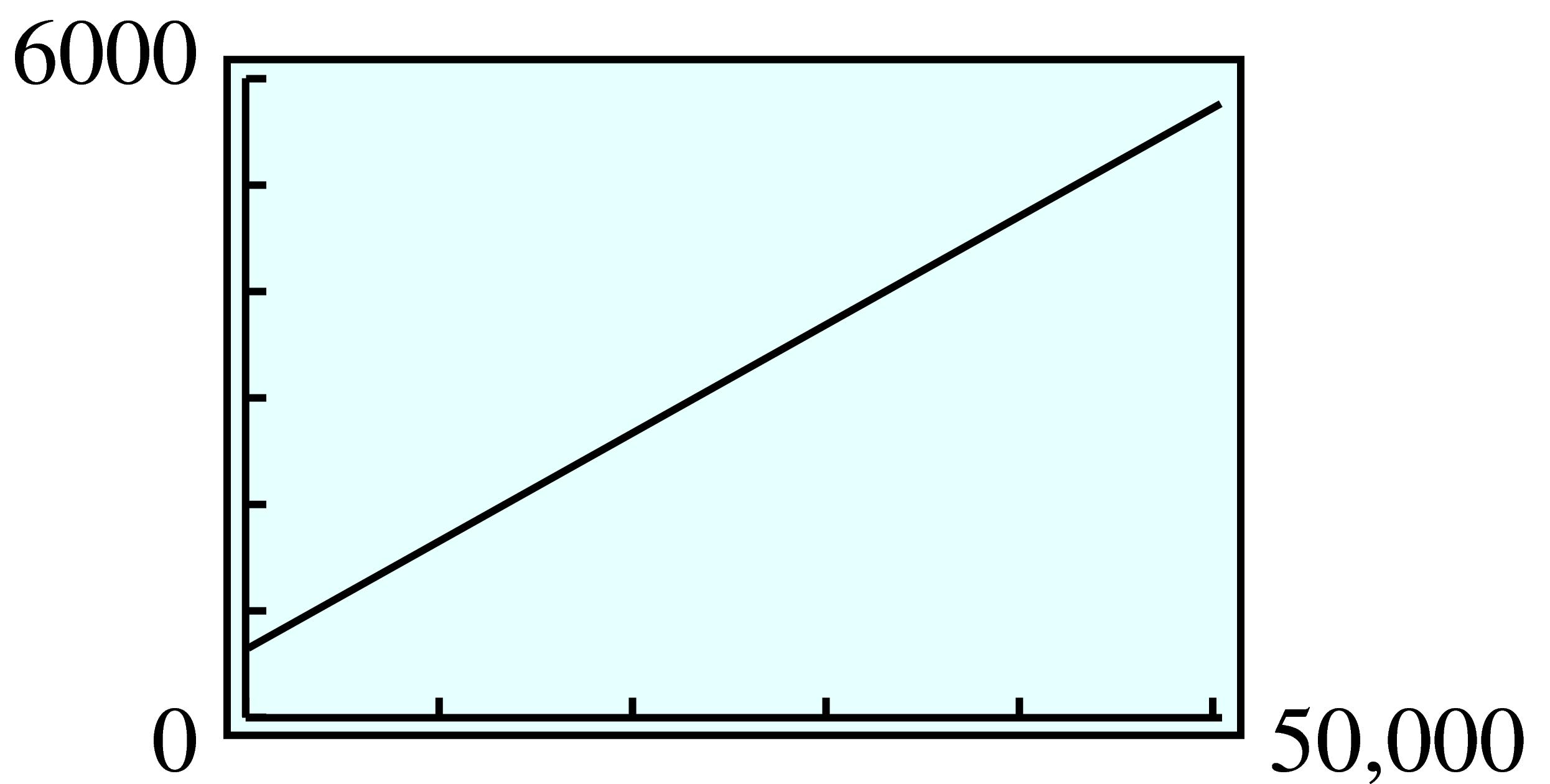
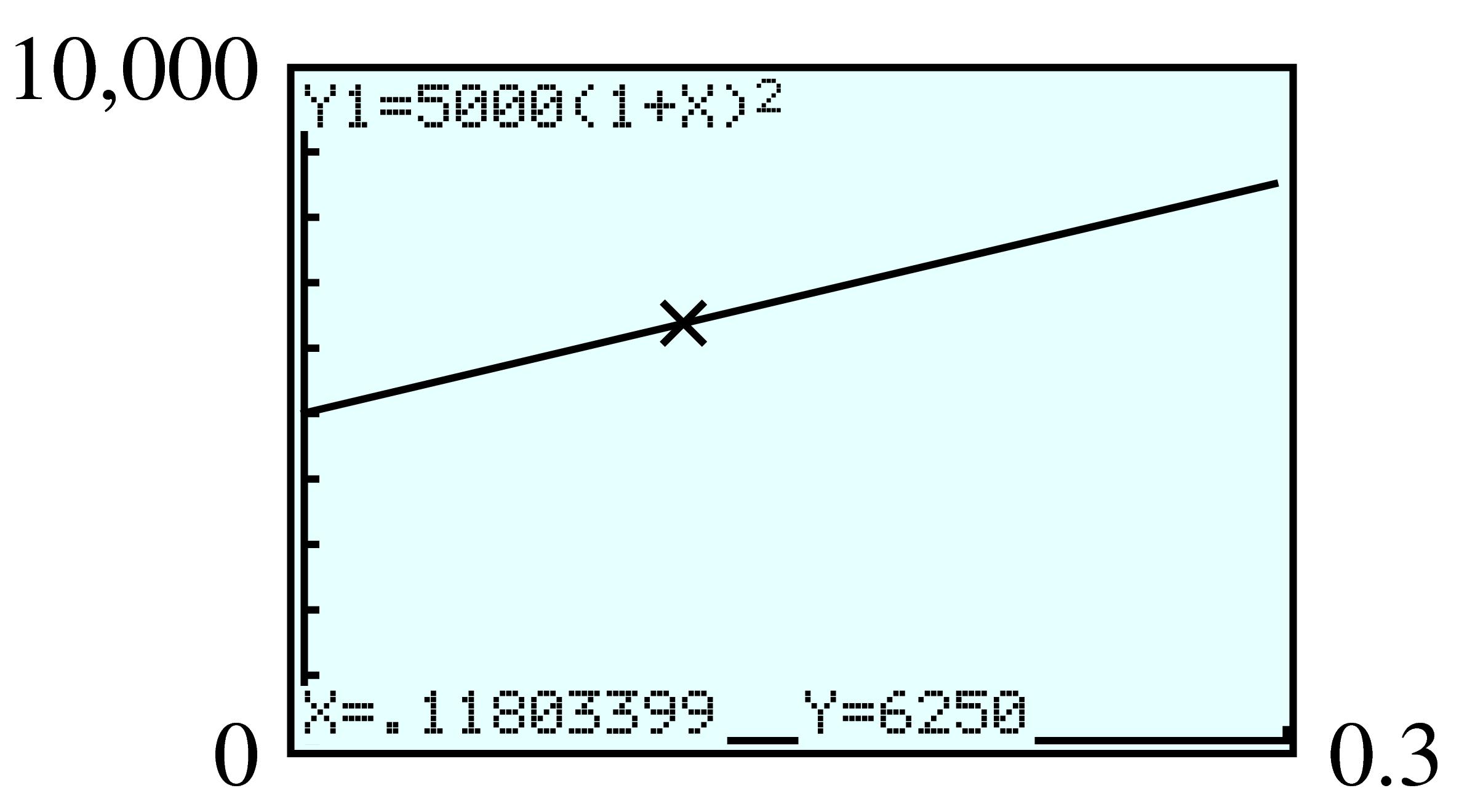
Miles Driven $4000$ $8000$ $12,000$ $16,000$ $20,000$

Cost ($) $5500$ $6000$ $6500$ $7000$ $7500$
$$500$
More than 16,000 miles

9.

Answer.

11.

Answer.

13.

Answer.

$\displaystyle (8, 0), (0, 4)$

15.

Answer.

$\displaystyle (4, 0), (0, -3)$

17.

Answer.

$\displaystyle (9, 0), (0, -4)$

19.

Answer.

$\displaystyle (-2250, 0), (0, 1500)$

21.

Answer.

$\displaystyle (12, 0), (0, 4)$

23.

Answer.

$\displaystyle \left(\dfrac{3}{2} , 0\right), \left(0, \dfrac{11}{3} \right)$

25.

Answer.

$$2.40x,$ $$3.20y$
$\displaystyle 2.40x + 3.20y = 19,200$
The $y$-intercept, $6000$ gallons, is the amount of premium that the gas station owner can buy if he buys no regular. The $x$-intercept, $8000$ gallons, is the amount of regular he can buy if he buys no premium.

27.

Answer.

$9x$ mg, $4y$ mg
$\displaystyle 9x + 4y = 1800$
The $x$-intercept, $200$ grams, tells how much fig Delbert should eat if he has no bananas, and the $y$-intercept, $450$ grams, tells how much banana he should eat if he has no figs.

29.

Answer.

$\displaystyle (3,0), (0,5) $
$\displaystyle \left(\dfrac{1}{2},0\right), \left(0,\dfrac{-1}{4}\right) $
$\displaystyle \left(\dfrac{5}{2},0\right), \left(0,\dfrac{-3}{2}\right) $
$\displaystyle (p,0), (0,q) $
The value of $a$ is the $x$-intercept, and the value of $b$ is the $y$-intercept.

31.

Answer.

$\displaystyle (0, b)$
$\left(\dfrac{-b}{m},0\right)\text{,}$ if $m\ne 0$

33.

Answer.

$-2x + 3y = 2400$

35.

Answer.

$3x + 400y = 240$

37.

Answer.

$\displaystyle y = 6 - 2x$

39.

Answer.

$\displaystyle y = \dfrac{3}{4}x-300$

41.

Answer.

$\displaystyle y = 0.02 - 0.04x$

43.

Answer.

$\displaystyle y = 210 - 35x$

45.

Answer.

$\displaystyle (100, 0), (0, 25)$
$\displaystyle y = 25 - \dfrac{1}{4}x$

47.

Answer.

$\displaystyle (0.04, 0), (0, -0.05)$
$\displaystyle y = 1.25x - 0.05$

49.

Answer.

$\displaystyle (-60, 0), (0, 12)$
$\displaystyle y = 12 + \dfrac{1}{5}x$

51.

Answer.

$\displaystyle (-42, 0), (0, -28)$
$\displaystyle y = \dfrac{-2}{3}x-28$

1.2 Functions
Homework 1.2

1.

Answer.

Function; the tax is determined by the price of the item.

3.

Answer.

Not a function; incomes may differ for same number of years of education.

5.

Answer.

Function; weight is determined by volume.

7.

Answer.

Input: items purchased; output: price of item. Yes, a function because each item has only one price.

9.

Answer.

Input: topics; output: page or pages on which topic occurs. No, not a function because the same topic may appear in more than one page.

11.

Answer.

Input: students’ names; output: students’ scores on quizzes, tests, etc. No, not a function because the same student can have different grades on different tests.

13.

Answer.

Input: person stepping on scales; output: person’s weight. Yes, a function because a person cannot have two different weights at the same time.

15.

Answer.

17.

Answer.

Yes

19.

Answer.

Yes

21.

Answer.

Yes

23.

Answer.

25.

Answer.

Yes

27.

Answer.

$\displaystyle 60$
$\displaystyle 37.5$
$\displaystyle 30$

29.

Answer.

$\displaystyle 15\%$
$\displaystyle 14\%$
$7010–$9169

31.

Answer.

$67.7\text{:}$ In 1985, $67.7\%$ of 20–24 year old women had not yet had children.
1987: Approximately $68\%$ of 20–24 year old women had not yet had children in 1987.
$\displaystyle f (1997) = 64.9$

33.

Answer.

No
60; no
Decreasing

35.

Answer.

1991
1 yr
1 yr
About 7300

37.

Answer.

Approximately $$1920$
$$5$ or $$15$
$\displaystyle 7.50\lt d\lt 12.50$

39.

Answer.

1968, about $$8.70$
1989, about $$5.10$
1967, approximately 1970

41.

Answer.

$\displaystyle 0$
$\displaystyle 10$
$\displaystyle -19.4$
$\displaystyle \dfrac{14}{3} $

43.

Answer.

$\displaystyle 1$
$\displaystyle 6$
$\displaystyle \dfrac{3}{8}$
$\displaystyle 96.48 $

45.

Answer.

$\displaystyle \dfrac{5}{6} $
$\displaystyle 9$
$\displaystyle \dfrac{-1}{10}$
$\displaystyle \dfrac{12}{13}\approx 0.923 $

47.

Answer.

$\displaystyle \sqrt{12} $
$\displaystyle 0$
$\displaystyle \sqrt{3}$
$\displaystyle \sqrt{0.2}\approx 0.447 $

49.

Answer.

$V(12) = 1120\text{:}$ After 12 years, the SUV is worth $$1120\text{.}$
$t = 12.5\text{:}$ The SUV has zero value after $12\frac{1}{2}$ years.
The value 2 years later

51.

Answer.

$N(6000) = 2000\text{:}$ $2000$ cars will be sold at a price of $$6000\text{.}$
$N(p)$ decreases with increasing $p$ because fewer cars will be sold when the price increases.
$2N(D)$ represents twice the number of cars that can be sold at the current price.

53.

Answer.

$v(250) = 54.8$ is the speed of a car that left $250$-foot skid marks.
$833\dfrac{1}{3}$ feet
$\displaystyle v\left(833\dfrac{1}{3}\right)= 100$

55.

Answer.

June 21–24, June 29–July 3, July 8–14
June 17–21, June 25–29, July 4–7
June 22–24, June 27, June 29–July 4, July 8–14
Avalanches occur when temperatures rise above freezing immediately after snowfall.

57.

Answer.

No
Yes
Moving downwards on the graph corresponds to moving downwards in the ocean.

59.

Answer.

$\displaystyle 27a^2 - 18a$
$\displaystyle 3a^2 + 6a$
$\displaystyle 3a^2 - 6a + 2$
$\displaystyle 3a^2 + 6a $

61.

Answer.

$\displaystyle 8$
$\displaystyle 8$
$\displaystyle 8$
$\displaystyle 8 $

63.

Answer.

$\displaystyle 8x^3 - 1$
$\displaystyle 2x^3 - 2$
$\displaystyle x^6 - 1$
$\displaystyle x^6 - 2x^3 + 1 $

65.

Answer.

$\displaystyle a^6$
$\displaystyle a^{12}$
$\displaystyle a^3b^3$
$\displaystyle a^3 + 3a^2b + 3ab^2 + b^3 $

67.

Answer.

$\displaystyle 96a^5$
$\displaystyle 6a^5$
$\displaystyle 3a^{10}$
$\displaystyle 9a^{10} $

69.

Answer.

$\displaystyle 11$
$\displaystyle 13$
$\displaystyle 3a + 3b - 4$
$\displaystyle 3a + 3b - 2 $

This function does NOT satisfy $f (a + b) = f (a) + f (b)\text{.}$

71.

Answer.

$\displaystyle 19$
$\displaystyle 28$
$\displaystyle a^2 + b^2 + 6$
$\displaystyle a^2 + 2ab + b^2 + 3 $

This function does NOT satisfy $f (a + b) = f (a) + f (b)\text{.}$

73.

Answer.

$\displaystyle \sqrt{3}+2 $
$\displaystyle \sqrt{6} $
$\displaystyle \sqrt{a+1}+\sqrt{b+1} $
$\displaystyle \sqrt{a+b+1} $

This function does NOT satisfy $f (a + b) = f (a) + f (b)\text{.}$

75.

Answer.

$\displaystyle \dfrac{-5}{3} $
$\displaystyle \dfrac{-2}{5} $
$\displaystyle \dfrac{-2}{a}-\dfrac{-2}{b} $
$\displaystyle \dfrac{-2}{a+b} $

This function does NOT satisfy $f (a + b) = f (a) + f (b)\text{.}$

77.

Answer.

$x$ $0$ $10$ $20$ $30$ $40$ $50$ $60$ $70$ $80$ $90$ $100$

$f(x)$ $800$ $840$ $840$ $800$ $720$ $600$ $440$ $240$ $0$ $-280$ $-600$

$a = 50$ and $b = 60$
$x$ $50$ $51$ $52$ $53$ $54$ $55$ $56$ $57$ $58$

$f(x)$ $600$ $585.8$ $571.2$ $556.2$ $540.8$ $525$ $508.8$ $492.2$ $475.2$

$c = 56$ and $d = 57$
$x$ $56$ $56.1$ $56.2$ $56.3$ $56.4$ $56.5$ $56.6$

$f(x)$ $508.8$ $507.158$ $505.512$ $503.862$ $502.208$ $500.55$ $498.888$

$p = 56.5$ and $q = 56.6$
$\displaystyle s = 56.55$
$\displaystyle f (56.55) = 499.7195$

79.

Answer.

$94.85$

1.3 Graphs of Functions
Homework 1.3

1.

Answer.

$\displaystyle -2, 0,5$
$\displaystyle 2$
$\displaystyle h(-2)=0,~h(1)=0,~h(0)=-2$
$\displaystyle 5$
$\displaystyle 3$
Increasing: $(-3,0)$ and $(1,3)\text{;}$ decreasing: $(0,1)$ and $(3,5)$

3.

Answer.

$\displaystyle -1, 2$
$\displaystyle 3, -1.3$
$R(-2) = 0\text{,}$ $R(2) = 0\text{,}$ $R(4) = 0\text{,}$ $R(0) = 4$
Max: $4\text{;}$ min: $-5$
Max at $p = 0\text{;}$ min at $p = 5$
Increasing: $(-3, 0)$ and $(1, 3)\text{;}$ decreasing: $(0, 1)$ and $(3, 5)$

5.

Answer.

$\displaystyle 0, \dfrac{1}{2}, 0$
$\displaystyle 0.9$
$\dfrac{-5}{6}\text{,}$ $\dfrac{-1}{6}\text{,}$ $\dfrac{7}{6}\text{,}$ $\dfrac{11}{6}$
Max: $1\text{;}$ min: $-1$
Max at $x=-1.5, 0.5\text{;}$ min at $x=-0.5, 1.5$

7.

Answer.

$\displaystyle 2, 2, 1$
$-6 \le s \lt -4~$ or $~0\le s\lt 2$
Max: $2\text{;}$ min: $-1$
Max for $-3\le s\lt -1~$ or $~3\le s\lt 5\text{;}$ min for $-6\le s\lt -4~$ or $~0\le s\lt 2$

9.

Answer.

(a) and (d)

11.

Answer.

13.

Answer.

15.

Answer.

17.

Answer.

$f (1000) = 1495\text{:}$ The speed of sound at a depth of $1000$ meters is approximately $1495$ meters per second.
$d = 570$ or $d = 1070\text{:}$ The speed of sound is $1500$ meters per second at both a depth of $570$ meters and a depth of $1070$ meters.
The slowest speed occurs at a depth of about $810$ meters and the speed is about $1487$ meters per second, so $f (810) = 1487\text{.}$
$f$ increases from about $1533$ to $1541$ in the first $110$ meters of depth, then drops to about $1487$ at $810$ meters, then rises again, passing $1553$ at a depth of about $1600$ meters.

19.

Answer.

$f(1985)=41\text{:}$ The federal debt in $1985$ was about $41\%$ of the gross domestic product.
$t = 1942$ or $t = 1955\text{:}$ The federal debt was $70\%$ of the gross domestic product in $1942$ and $1955\text{.}$
In about $1997\text{,}$ the debt was about $67\%$ of the gross domestic product, so $f (1997)\approx 67.3\text{.}$
The percentage basically dropped from 1946 to 1973, but there were small rises around 1950, 1954, 1958, and 1968, so the longest time interval was from 1958 to 1967.

21.

Answer.

1. $\displaystyle x = -3$
2. $\displaystyle x\lt -3$
3. $\displaystyle x\gt -3$
1. $\displaystyle x = -3$
2. $\displaystyle x\lt -3$
3. $\displaystyle x\gt -3$
On the graph of $y=-2x + 6\text{,}$ a value of $y$ is the same as a value of $-2x + 6\text{,}$ so parts (a) and (b) are asking for the same $x$’s.

23.

Answer.

$\displaystyle x = 0.6$
$\displaystyle x=-0.4$
$\displaystyle x\gt 0.6$
$\displaystyle x\lt -0.4$

25.

Answer.

$x=-1$ or $x = 1$
Approximately $-3\le x\le -2$ or $2\le x\le 3$

27.

Answer.

$\displaystyle 3.5$
$\displaystyle -2.2, -1.2, 3.4$
$p\lt -3.1$ or $0.3\lt p\lt 2.8$
$\displaystyle 0.5\lt B\lt 5.5$
$p\lt -1.7$ or $p\gt 1.7$

29.

Answer.

1. $\displaystyle -2, 2$
2. $\displaystyle -2.8, 0, 2.8$
3. $-2.5\lt q\lt-1.25$ or $1.25\lt q\lt 2.5$
$-2 \lt q\lt 0$ or $q\gt 2$

31.

Answer.

He has an error: $f(-3)$ cannot have both the value $5$ and also the value $-2\text{,}$ and $f(-1)$ cannot have both values $2$ and $-4\text{.}$
Her readings are possible for a function: each input has only one output.

33.

Answer.

$x$ $-4$ $-2$ $3$ $5$

$g(x)$ $4.5$ $5.7$ $5.2$ $3.3$
$\displaystyle -4.8, 4.8$

35.

Answer.

$\displaystyle (-1.6, 4.352), (1.6, -4.352)$
$F(-1.6) = 4.352\text{;}$ $F(1.6) = -4.352$

37.

Answer.

The curve cannot be distinguished from the $x$-axis in the standard window because the values of $y$ are closer to zero than the resolution of the calculator can display. The second window provides sufficient resolution to see the curve.

39.

Answer.

The curve looks like two vertical lines in the standard window because that window covers too small a region of the plane. The second window allows us to see the turning points of the curve.

41.

Answer.

$\displaystyle x = 4$
$\displaystyle x = -5$
$\displaystyle x\gt 1$
$\displaystyle x\lt 14 $

43.

Answer.

$\displaystyle x = 11$
$\displaystyle x = -10$
$\displaystyle x\ge -5$
$\displaystyle x\le 8 $

45.

Answer.

$\displaystyle x = 4 $
$\displaystyle x\lt 22 $

47.

Answer.

$\displaystyle x = 20 $
$\displaystyle x\le 7 $

49.

Answer.

$\displaystyle -15, 5, 20 $
$\displaystyle -13, 2, 22 $

1.4 Slope and Rate of Change
Homework 1.4

1.

Answer.

Anthony

3.

Answer.

Bob’s driveway

5.

Answer.

$-1$

7.

Answer.

$\dfrac{-2}{3}$

9.

Answer.

$\displaystyle \dfrac{3}{4} $

11.

Answer.

$\displaystyle -3$

13.

Answer.

$\displaystyle \dfrac{8}{5} $

15.

Answer.

17.

Answer.

1. $\displaystyle -3$
2. $\displaystyle 6$
3. $\displaystyle \dfrac{-3}{2} $
4. $\displaystyle \dfrac{9}{2}$
1. $\displaystyle -4$
2. $\displaystyle 8$
3. $\displaystyle \dfrac{8}{3} $
4. $\displaystyle \dfrac{4}{3}$

19.

Answer.

$\dfrac{100}{7}$ ft $\approx 14.286$ ft $\approx 14$ ft $~3.4$ in

21.

Answer.

23.

Answer.

$\dfrac{3}{4} $

25.

Answer.

$-4000$

27.

Answer.

$\displaystyle \dfrac{5}{2} $
$x$ $y$

$3$ $\frac{7}{2}$

$6$ $11$

29.

Answer.

$\displaystyle -3 $
$x$ $y$

$-1$ $\alert{30}$

$\alert{5}$ $12$

31.

Answer.

$t$ $4$ $8$ $20$ $40$

$S$ $32 $ $64$ $160$ $320$
8 dollars/hour
The typist is paid $$8$ per hour.

33.

Answer.

$1250$ barrels/day
The slope indicates that oil is pumped at a rate of $1250$ barrels per day.

35.

Answer.

$-6$ liters/day
The slope indicates that the water is diminishing at a rate of $6$ liters per day.

37.

Answer.

$12$ inches/foot
The slope gives the conversion rate of 12 inches per foot.

39.

Answer.

$4$ dollars/kilogram
The slope gives the unit price of $\$4$ per kilogram

41.

Answer.

(a)

43.

Answer.

Yes, the slope between any two points is $\frac{1}{2}\text{.}$
$0.5$ grams of salt per degree Celsius

45.

Answer.

Yes
$\displaystyle 2\pi$

47.

Answer.

$\displaystyle \dfrac{1500\text{ meters}}{1 \text{ second}} $
$3375$ meters

49.

Answer.

The distances are known.
$5.7$ km per second

51.

Answer.

About $18\degree$C
0.3 km to 0.4 km
About $-28\degree$C per kilometer

53.

Answer.

$\displaystyle -3$
$\displaystyle 2$

55.

Answer.

$\displaystyle \dfrac{-1}{4} $
$\displaystyle -1$

57.

Answer.

$(1,F(1)),(4,F(4))\text{;}$ $~~~~F(4) - F(1)$
$(r,f(r)),(s,f(s))\text{;}$ $~~~~f(s) - f(r)$

59.

Answer.

$(2,H(2)),(3,H(3))\text{;}$ $~~~~H(3) - H(2)$
$(a,g(a)),(b,g(b))\text{;}$ $~~~~g(b) - g(a)$

61.

Answer.

$(c,s(c)),(d,s(d))\text{;}$ $~~~~s(c)(d - c)$
$(x_1,q(x_1)),(x_2,q(x_2))\text{;}$ $~~~~q(x_2)(x_2 - x_1)$

63.

Answer.

$(1, f (1)), (5, f (5))\text{;}$ $~~~~\dfrac{f (5) - f (1)}{4}$
$(-1, f (-1)), (2, f (2))\text{;}$ $~~~~\dfrac{f (2) - f (-1)}{3}$

65.

Answer.

$(a, f (a)), (b, f (b))\text{;}$ $~~~~\dfrac{f(b) - f(a)}{b-a}$
$(a, f (a)), (a+\Delta x, f(a+\Delta x))\text{;}$ $~~~~\dfrac{f(a+\Delta x) - f(a)}{\Delta x}$

1.5 Linear Functions
Homework 1.5

1.

Answer.

$\displaystyle y = \dfrac{1}{2}- \dfrac{3}{2}x$
Slope $\dfrac{-3}{2}\text{,}$ $y$-intercept $\dfrac{1}{2} $

3.

Answer.

$\displaystyle y = \dfrac{1}{9}- \dfrac{1}{6}x$
Slope $\dfrac{-1}{6}\text{,}$ $y$-intercept $\dfrac{1}{9} $

5.

Answer.

$\displaystyle y = -22 + 14x$
Slope $14\text{,}$ $y$-intercept $-22 $

7.

Answer.

$\displaystyle y = -29$
Slope $0\text{,}$ $y$-intercept $-29 $

9.

Answer.

$\displaystyle y =\dfrac{49}{3}-\dfrac{5}{3}x $
Slope $\dfrac{-5}{3}\text{,}$ $y$-intercept $\dfrac{49}{3} $

11.

Answer.

$\displaystyle y = -2 + 3x$
$\displaystyle \dfrac{2}{3} $

13.

Answer.

$\displaystyle y = -6 + \dfrac{5}{3}x$
$\displaystyle \dfrac{-18}{5} $

15.

Answer.

$5$

17.

Answer.

$\dfrac{-1}{4} $

19.

Answer.

$m =\dfrac{-A}{B}\text{,}$ $x$-intercept $\left(\dfrac{C}{A},0\right) \text{,}$ $y$-intercept $\left(0,\dfrac{C}{B}\right) $

21.

Answer.

$\displaystyle a = 100 + 150t$
The slope tells us that the skier’s altitude is increasing at a rate of $150$ feet per minute, the vertical intercept that the skier began at an altitude of $200$ feet.

23.

Answer.

$\displaystyle G = 25 + 12.5t$
The slope tells us that the garbage is increasing at a rate of $12.5$ tons per year, the vertical intercept that the dump already had $25$ tons (when the new regulations went into effect).

25.

Answer.

$\displaystyle M = 7000 - 400w$
The slope tells us that Tammy’s bank account is diminishing at a rate of $$400$ per week, the vertical intercept that she had $$7000$ (when she lost all sources of income).

27.

Answer.

$50\degree$F
$-20\degree$C
The slope, $\frac{9}{5} = 1.8\text{,}$ tells us that Fahrenheit temperatures increase by $1.8\degree$ for each increase of $1\degree$ Celsius.
$C$-intercept $\left(-17\frac{7}{9}, 0\right)\text{:}$ $-17\frac{7}{9}\degree$ C is the same as $0\degree$F; $F$-intercept $(0, 32)\text{:}$ $0\degree$C is the same as $32\degree$F.

29.

Answer.

$\displaystyle m = 25, ~b = 250$
$\displaystyle y = 250 + 25x$

31.

Answer.

$\displaystyle y = 0.12x + 25.4$
$18$ kg

33.

Answer.

$\displaystyle y + 5 = -3(x - 2)$
$\displaystyle y = 1 - 3x$

35.

Answer.

$\displaystyle y + 1 = \frac{5}{3}(x - 2)$
$\displaystyle y = \frac{-13}{3} + \frac{5}{3}x$

37.

Answer.

$\displaystyle y + 3.5 = -0.25(x + 6.4)$
$\displaystyle y = -5.1 - 0.25x$

39.

Answer.

$\displaystyle y + 250 = 2.4(x - 80)$
$\displaystyle y = -442 + 2.4x$

41.

Answer.

$\displaystyle m =\dfrac{2}{3}$
$\displaystyle y=\dfrac{-1}{3}+ \dfrac{2}{3}x$

43.

Answer.

$(-4, 4)\text{:}$ neither; $(0, 3)\text{:}$ $y = px + q\text{;}$ $(3, 2)\text{:}$ both; $(2, 1)\text{:}$ neither; $(1,-2)\text{:}$ $y = tx + v$
$p =\dfrac{-1}{3}\text{,}$ $q = 3\text{,}$ $t = 2\text{,}$ $v = -4$

45.

Answer.

$\displaystyle m = 4, ~b = 40$
$\displaystyle y = 40 + 4x$

47.

Answer.

$\displaystyle m = -80, ~b = -2000$
$\displaystyle P = -2000 - 80t$

49.

Answer.

$\displaystyle m = \dfrac{1}{4}, ~b = 0$
$\displaystyle V = \dfrac{1}{4}d$

51.

Answer.

$y = \dfrac{3}{4}x\text{,}$ $y = 1 + \dfrac{3}{4}x\text{,}$ $y = -2.7 + \dfrac{3}{4}x$
The lines are parallel.

53.

Answer.

55.

Answer.

57.

Answer.

$m = 2\text{;}$ $(6,-1)$

59.

Answer.

$m =\dfrac{-4}{3} \text{;}$ $(-5, 3)$

61.

Answer.

The lines with slope $3$ and $\frac{-1}{3}$ are perpendicular to each other, and the lines with slope $-3$ and $\frac{1}{3}$ are perpendicular to each other.

63.

Answer.

$m = -0.0018$ degree/foot, so the boiling point drops with altitude at a rate of $0.0018$ degree per foot. $b = 212\text{,}$ so the boiling point is $212\degree$ at sea level (where the elevation $h = 0$).

1.6 Linear Regression
Homework 1.6

1.

Answer.

$x$ $50$ $125$

$y$ $9000$ $15,000$
$\displaystyle C = 5000 + 80x$
$m = 80$ dollars/bike, so it costs the company $$80$ per bike it manufactures.

3.

Answer.

$g$ $12$ $5$

$d$ $312$ $130$
$\displaystyle d = 26g$
$m = 26$ miles/gallon, so the Porche’s fuel efficiency is $26$ miles per gallon.

5.

Answer.

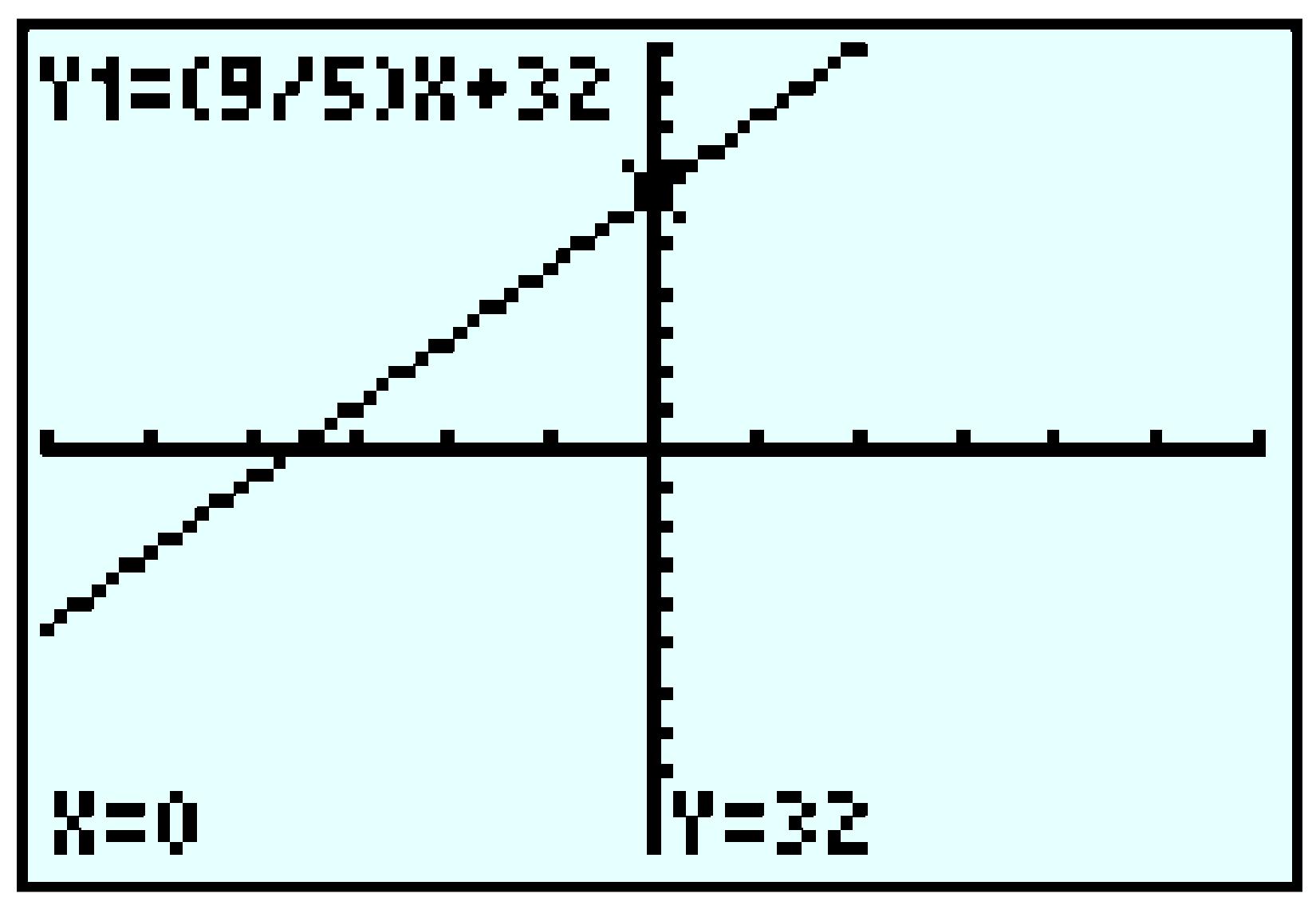
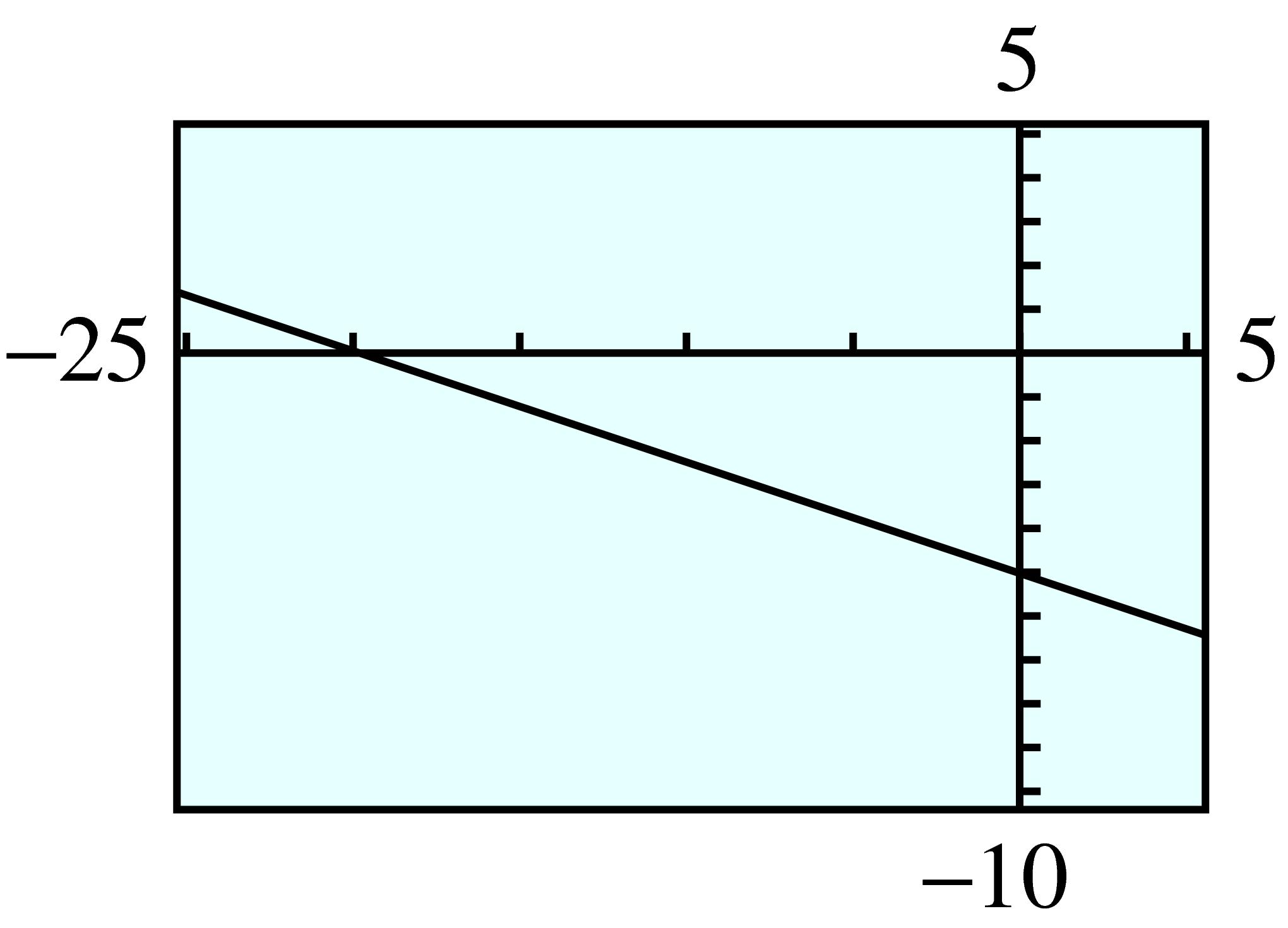
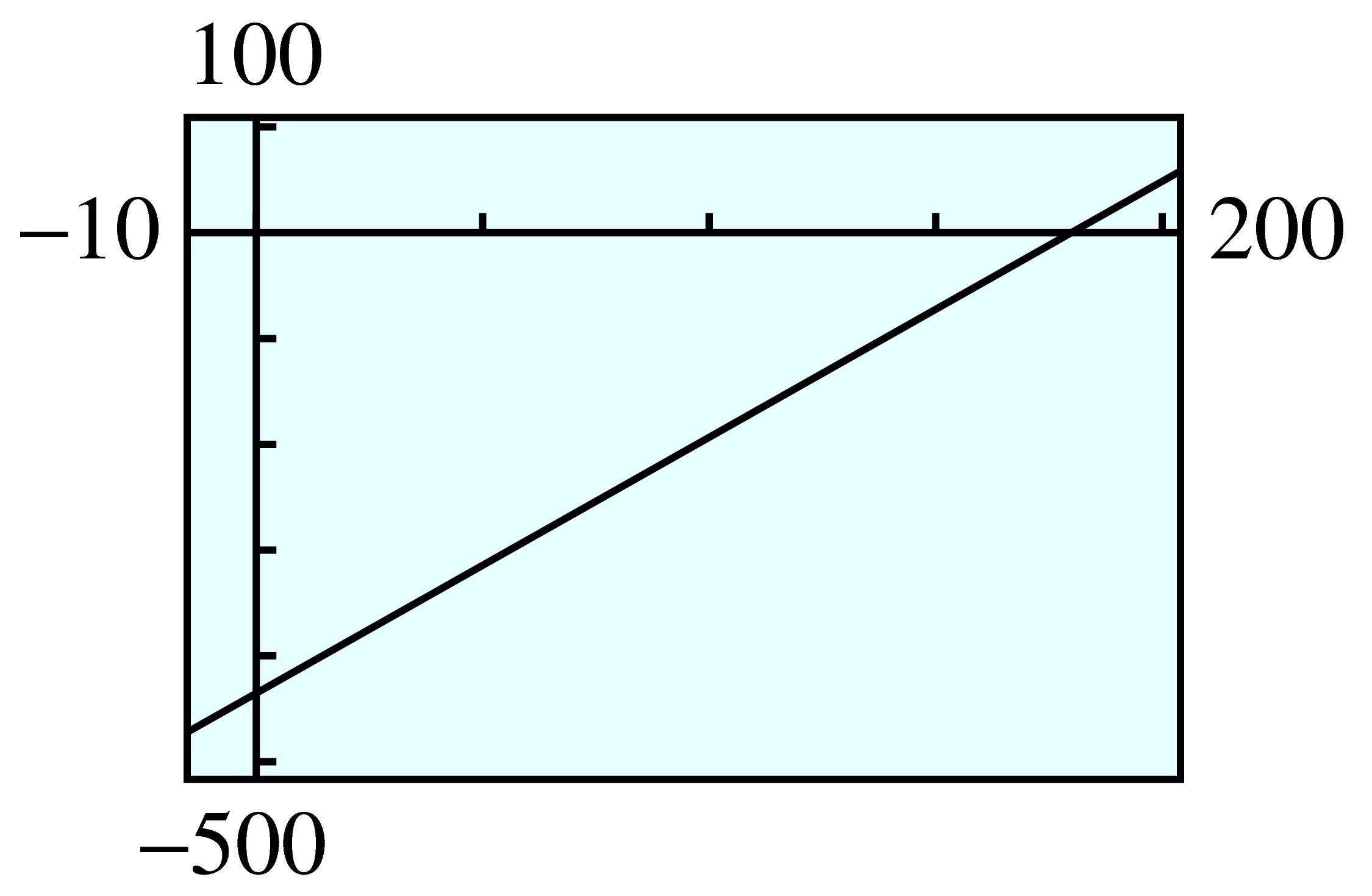
$C$ $15$ $-5$

$F$ $59$ $23$
$\displaystyle F=32+\dfrac{9}{5}C $
$m =\dfrac{9}{5} \text{,}$ so an increase of $1\degree$C is equivalent to an increase of $\dfrac{9}{5}\degree$F.

7.

Answer.

9.

Answer.

11.

Answer.

$12$ seconds
$\displaystyle 39$
$11.6$ seconds
$\displaystyle y = 8.5 + 0.1x$
$12.7$ seconds; $10.18$ seconds; The prediction for the 40-year-old is reasonable, but not the prediction for the 12-year-old.

13.

Answer.

$\displaystyle y = 121 + 19.86t$
$\displaystyle 419 $

15.

Answer.

$\displaystyle y = 64.2 - 1.63t$
$58$ births per $1000$ women
$32$ births per $1000$ women

17.

Answer.

$\displaystyle y = 0.18t + 67.9$
$74.9$ years
$79$ years

19.

Answer.

$\displaystyle y = 90.49t - 543.7$
$90.49$ dollars/year: Each additional year of education corresponds to an additional $$90.49$ in weekly earnings.
No: The degree or diploma attained is more significant than the number of years. So, for example, interpolation for the years of education between a bachelor’s and master’s degree may be inaccurate because earnings with just the bachelor’s degree will not change until the master’s degree is attained. And the years after the professional degree will not add significantly to earnings, so extrapolation is inappropriate.

21.

Answer.

$\displaystyle y = 1.6 + 0.11t$
$6.2$ billion tons

23.

Answer.

$0.34$ meters per year
$y = 0.34x$ ($b = 0$ because the plant has zero size until it begins.)
Over $1300$ years

25.

Answer.

Yes
$\displaystyle y = 1.29x - 1.62$
The slope, $1.29$ kg/sq cm, tells us that strength increases by $1.29$ kg when the muscle cross-sectional area increases by $1$ sq cm.

27.

Answer.

E
$y = 1.33x\text{;}$ There should be no loss in mass when no gas evaporates.
$1333$ mg
Oxygen

29.

Answer.

$75\degree$F
The slope of $-2$ degrees/hour says that temperatures are dropping at a rate of $2\degree$ per hour.

31.

Answer.

$20$ mph
The slope of $10$ mph/second says the car accelerates at a rate of $10$ mph per second.

33.

Answer.

2 min: $21\degree$C; 2 hr: $729\degree$C; The estimate at 2 minutes is reasonable; the estimate at 2 hours is not reasonable.

35.

Answer.

$128$ lb.

37.

Answer.

$\displaystyle y \approx -0.54x + 58.7$
$\displaystyle 31.7\%$
$90$ meters
The regression line gives a negative probability, which is not reasonable.

39.

Answer.

$\displaystyle y \approx 22.8x + 198.5$
$\approx 540$ watts
$198.5$ watts
$\approx -8.7$ newtons
$3.5$ watts
about $0.018$ or $1.8\%$

1.7 Chapter Summary and Review
Chapter 1 Review Problems

1.

Answer.

$n$ $100$ $500$ $800$ $1200$ $1500$

$C$ $4000$ $12,000$ $18,000$ $26,000$ $32,000$
$\displaystyle C = 20n + 2000$
$$22,000$
$\displaystyle 400$

3.

Answer.

$\displaystyle R = 2100 - 28t$
$(75, 0)\text{,}$ $(0, 2100)$
$t$-intercept: The oil reserves will be gone in 2080; $R$-intercept: There were $2100$ billion barrels of oil reserves in 2005.

5.

Answer.

$\displaystyle 2C + 5A = 1000$
$(500, 0)\text{,}$ $(0, 200)$
$C$-intercept: If no adult tickets are sold, he must sell $500$ children’s tickets; $A$-intercept: If no children’s tickets are sold, he must sell $200$ adult tickets.

7.

Answer.

9.

Answer.

11.

Answer.

13.

Answer.

15.

Answer.

A function: Each $x$ has exactly one associated $y$-value.

17.

Answer.

Not a function: The IQ of $98$ has two possible SAT scores.

19.

Answer.

$N(10) = 7000\text{:}$ Ten days after the new well is opened, the company has pumped a total of $7000$ barrels of oil.

21.

Answer.

Function

23.

Answer.

Not a function

25.

Answer.

$F(0) = 1, ~~F(-3) =\sqrt{37}$

27.

Answer.

$h(8) = -6, ~~h(-8) = -14$

29.

Answer.

$\displaystyle f (-2) = 3, ~~f (2) = 5$
$\displaystyle t = 1, ~~t = 3$
$t$-intercepts $(-3, 0), (4, 0)\text{;}$ $f (t)$-intercept: $(0, 2)$
Maximum value of $5$ occurs at $t = 2$

31.

Answer.

$\displaystyle x = \dfrac{1}{2}= 0.5$
$\displaystyle x = \dfrac{27}{8}\approx 3.4$
$\displaystyle x \gt 4.9$
$\displaystyle x\le 2.0$

33.

Answer.

$\displaystyle x\approx\pm 5.8 $
$\displaystyle x = \pm 0.4$
$-2.5\lt x \lt 0$ or $0\lt x\lt 2.5$
$x\le -0.5$ or $x\ge 0.5$

35.

Answer.

$H(2a) =4a^2 + 4a, ~~H(a+1) =a^2+4a+3$

37.

Answer.

$f (a) + f (b) = 2a^2 + 2b^2 - 8, ~~f (a + b) = 2a^2 + 4ab + 2b^2 - 4$

39.

Answer.

The volleyball

41.

Answer.

Highway 33

43.

Answer.

$\displaystyle B = 800 - 5t$
$m = -5$ thousand barrels/minute: The amount of oil in the tanker is decreasing by $5000$ barrels per minute.

45.

Answer.

$\displaystyle F = 500 + 0.10C$
$m = 0.10\text{:}$ The fee increases by $\$0.10$ for each dollar increase in the remodeling job.

47.

Answer.

$\dfrac{-3}{2} $

49.

Answer.

$\dfrac{-34}{83}\approx-0.4 $

51.

Answer.

$80$ ft

53.

Answer.

$\displaystyle h(x_2) - h(x_1)$
$\displaystyle \dfrac{h(x_2) - h(x_1)}{x_2 - x_1} $

55.

Answer.

Neither

57.

Answer.

$d$	$V$
$-5$	$-4.8$
$-2$	$-3$
$1$	$-1.2$
$6$	$1.8$
$10$	$4.2 $

59.

Answer.

$m = \dfrac{1}{2}, ~b =\dfrac{-5}{4}$

61.

Answer.

$m = -4, ~b = 3$

63.

Answer.

$\displaystyle y = \dfrac{10}{3}- \dfrac{2}{3}x$

65.

Answer.

$\displaystyle m = -2, ~b = 3$
$\displaystyle y = 3 - 2x$

67.

Answer.

$\dfrac{3}{5} $

69.

Answer.

$\displaystyle \dfrac{3}{2} $
$(4,2)\text{,}$ no
$\displaystyle (6,5)$

71.

Answer.

$(3,-14), ~(-7, 2)$

73.

Answer.

$\displaystyle T = 62 - 0.0036h$
$-46\degree$F; $108\degree$F
$-71\degree$F

75.

Answer.

$y = \dfrac{2}{5}- \dfrac{9}{5}x$

77.

Answer.

$t$ $0$ $15$

$P$ $4800$ $6780$
$\displaystyle P = 4800 + 132t$
$m = 132$ people/year: the population grew at a rate of $132$ people per year.

79.

Answer.

$6$

81.

Answer.

$129$ lb, $145$ lb
$\displaystyle y = 2.\overline{6} x - 44.\overline{3}$
$137$ lb
$\displaystyle y=2.84x - 55.74$
$137.33$ lb

83.

Answer.

$45$ cm
$87$ cm
$\displaystyle y = 1.2x - 3$
$69$ cm
$y = 1.197x - 3.660\text{;}$ $68.16$ cm

2 Modeling with Functions
2.1 Nonlinear Models
Homework 2.1

1.

Answer.

$\pm\dfrac{5}{3} $

3.

Answer.

$\pm\sqrt{6} $

5.

Answer.

$\pm \sqrt{6} $

7.

Answer.

$\pm 2.65$

9.

Answer.

$\pm 5.72$

11.

Answer.

$\pm 5.73$

13.

Answer.

$\pm\sqrt{\dfrac{Fr}{m}} $

15.

Answer.

$\pm\sqrt{\dfrac{2s}{g}} $

17.

Answer.

$\displaystyle V = 2.8 \pi r^2\approx 8.8r^2$
$r$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$

$V$ $8.8$ $35.2$ $79.2$ $140.7$ $219.9$ $316.7$ $431.0$ $563.0$

The volume increases by a factor of $4\text{.}$
$5.86$ cm

19.

Answer.

$21$ in.

21.

Answer.

$\sqrt{1800}\approx 42.4$ m

23.

Answer.

$\sqrt{128}$ in. by $\sqrt{128}$ in. $\approx 11.3$ in. ${}\times{} 11.3$ in.

25.

Answer.

$\displaystyle x=\pm 12$

27.

Answer.

$x= 1$ or $x=9$

29.

Answer.

$x= 10$ or $x=-2$

31.

Answer.

$5, -1$

33.

Answer.

$\dfrac{5}{2}, \dfrac{-3}{2}$

35.

Answer.

$-2 \pm \sqrt{3}$

37.

Answer.

$\dfrac{1}{2} \pm \dfrac{\sqrt{3}}{2} $

39.

Answer.

$\dfrac{-2}{9} , \dfrac{-4}{9} $

41.

Answer.

$\dfrac{7}{8} \pm \dfrac{\sqrt{8}}{8}$

43.

Answer.

$6$

45.

Answer.

$64$

47.

Answer.

$\dfrac{13}{6} $

49.

Answer.

$8$

51.

Answer.

$9$

53.

Answer.

$\dfrac{33}{64} $

55.

Answer.

$\displaystyle B = 5000 (1 + r )^2$
$\displaystyle 11.8\%$

57.

Answer.

$8\%$

59.

Answer.

$7.98$ mm

61.

Answer.

$\sqrt{3}\approx 1.73$ sq cm, $4\sqrt{3}\approx 6.93$ sq cm, $25\sqrt{3}\approx 43.3$ sq cm
An equilateral triangle with side $5.1$ cm has area $11.263 \text{ cm}^2\text{.}$
$\text{side}\approx 6.8 $ cm
$\dfrac{\sqrt{3}}{4}s^2=20\text{;}$ $s \approx 6.8$
$\approx 20 $ cm

63.

Answer.

$\pm \sqrt{\dfrac{bc}{a}}$

65.

Answer.

$a \pm 4$

67.

Answer.

$\dfrac{-b\pm 3}{a} $

69.

Answer.

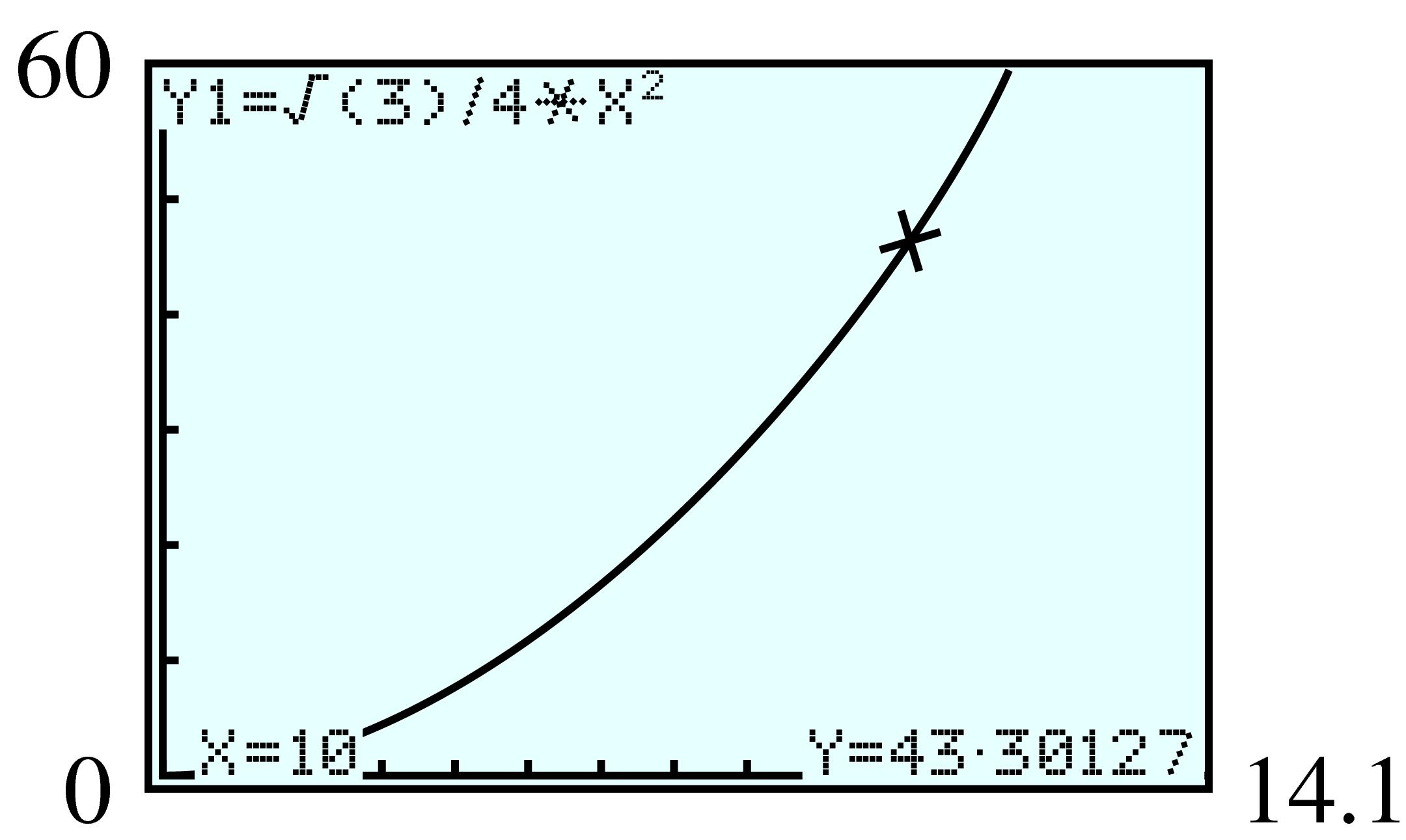
Height	Base	Area	Height	Base	Area
$1$	$34$	$34$	$10$	$16 $	$160$
$2$	$32$	$64$	$11$	$14$	$154$
$3$	$30$	$90$	$12$	$12$	$144$
$4$	$28$	$112$	$13$	$10$	$130$
$5$	$26$	$130$	$14$	$8$	$112$
$6$	$24$	$144$	$15$	$6$	$90$
$7$	$22$	$154$	$16$	$4$	$64$
$8$	$20$	$160$	$17$	$2$	$34$
$9$	$18$	$162$	$18$	$0$	$0$

$162$ sq ft, with base $18$ ft, height $9$ ft
Base: $36 - 2x\text{;}$ area: $x (36 - 2x)$
See (a)
$6.5$ ft or $11.5$ ft

71.

Answer.

$v$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$ $11$

$J$ $0$ $0.05$ $0.2$ $0.46$ $0.82$ $1.28$ $1.84$ $2.5$ $3.27$ $4.13$ $5.1$ $6.17$
$v$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$ $11$

$H$ $0.9$ $0.95$ $1.1$ $1.36$ $1.72$ $2.18$ $2.74$ $3.4$ $4.17$ $5.03$ $6.0$ $7.07$
$5.5$ meters
$10.15$ meters per second

2.2 Some Basic Functions
Homework 2.2

1.

Answer.

$\displaystyle -9$
$\displaystyle 9$

3.

Answer.

$\displaystyle -4$
$\displaystyle 20$

5.

Answer.

$-50 $

7.

Answer.

$144 $

9.

Answer.

$1 $

11.

Answer.

$\displaystyle 2.7$
$\displaystyle -2.7$
$\displaystyle 1.8$
$\displaystyle 2.9$

13.

Answer.

$\displaystyle 0.3$
$\displaystyle -0.4$
$\displaystyle 0.2$

15.

Answer.

$\displaystyle x = 0, ~x = 1$
$(-\infty,0) $ and $(0,1)$

17.

Answer.

$\displaystyle x = 1$
$\displaystyle (1, +\infty) $

19.

Answer.

Graph (b) is the basic graph shifted 2 units down; graph (c) is the basic graph shifted 1 unit up.

21.

Answer.

Graph (b) is the basic graph shifted 1.5 units left; graph (c) is the basic graph shifted 1 unit right.

23.

Answer.

Graph (b) is the basic graph reflected about the $x$-axis; graph (c) is the basic graph reflected about the $y$-axis.

25.

Answer.

$\displaystyle \sqrt{x} $
$\displaystyle \sqrt[3]{x} $
$\displaystyle \abs{x} $
$\displaystyle \dfrac{1}{x} $
$\displaystyle x^3 $
$\displaystyle \dfrac{1}{x^2} $

27.

Answer.

$\displaystyle x\approx 12$
$\displaystyle x\approx 18$
$\displaystyle x \lt 9$
$\displaystyle x\gt 3$

29.

Answer.

$\displaystyle t\approx -3.1$
$\displaystyle t\approx 1.5$
$\displaystyle t \lt 0.8$
$\displaystyle -2.4\lt t\lt 0.4$

31.

Answer.

$\displaystyle x = 41$
$\displaystyle 29\lt x\lt 61$

33.

Answer.

$x = -5$ or $x=17$
$\displaystyle -1\lt x\lt 13$

35.

Answer.

$x$ $4 $ $1 $ $\frac{1}{4} $ $0 $ $\frac{1}{4} $ $1 $ $4 $

$y$ $-2$ $-1 $ $-\frac{1}{2} $ $0 $ $\frac{1}{2} $ $1 $ $2 $
no

37.

Answer.

$x$ $2 $ $1 $ $\frac{1}{2} $ $0 $ $\frac{1}{2} $ $1 $ $2 $

$y$ $-2$ $-1 $ $-\frac{1}{2} $ $0 $ $\frac{1}{2} $ $1 $ $2 $
no

39.

Answer.

$x$ $-\frac{1}{2} $ $-1 $ $-2 $ undefined $2 $ $1 $ $\frac{1}{2} $

$y$ $-2$ $-1 $ $-\frac{1}{2} $ $0 $ $\frac{1}{2} $ $1 $ $2 $
yes

41.

Answer.

43.

Answer.

45.

Answer.

47.

Answer.

49.

Answer.

51.

Answer.

53.

Answer.

$f(x) = \begin{cases} 8-2x \amp x\lt 4\\ 2x-8 \amp x\ge 4 \end{cases}$

55.

Answer.

$g(t) = \begin{cases} -1-\dfrac{t}{3} \amp t\lt -3\\ 1+\dfrac{t}{3} \amp t\ge -3 \end{cases}$

57.

Answer.

$F(x) = \begin{cases} -x^3 \amp x\lt 0\\ x^3 \amp x\ge 0 \end{cases}$

59.

Answer.

Not always true: $f (1 + 2)\ne f (1) + f (2)$ because $9\ne 5\text{.}$
True: $(ab)^2 = a^2b^2$

61.

Answer.

Not always true: $f (1 + 2)\ne f (1) + f (2)$ because $\frac{1}{3} \ne\frac{3}{2} \text{.}$
True: $\dfrac{1}{ab} = \dfrac{1}{a}\cdot\dfrac{1}{b} $

63.

Answer.

Not always true (unless $b=0$): $f (1 + 2)\ne f (1) + f (2)$ because $3m+b \ne 3m+2b \text{.}$
Not always true: $f (1\cdot 2)\ne f (1)\cdot f (2)$ because $2m+b \ne 2m^2 + 3mb + b^2 \text{.}$

65.

Answer.

67.

Answer.

The distributive law shows a relationship between multiplication and addition that always holds. The equation $f (a + b) = f (a) + f (b)$ is not about multiplication and may or may not be true.

2.3 Transformations of Graphs
Homework 2.3

1.

Answer.

$y=\sqrt{x+2} $

3.

Answer.

$y=x^3-1 $

5.

Answer.

$y=\dfrac{1}{x-4} $

7.

Answer.

Translate $y =\abs{x}$ by $2$ units down.

9.

Answer.

Translate $y =\sqrt[3]{s} $ by $4$ units right.

11.

Answer.

Translate $y =\dfrac{1}{t^2} $ by $1$ unit up.

13.

Answer.

Translate $y =r^3 $ by $2$ units left.

15.

Answer.

Translate $y =\sqrt{d} $ by $3$ units down.

17.

Answer.

Translate $y =\dfrac{1}{v} $ by $6$ units left.

19.

Answer.

A vertical stretch by a factor of $3\text{:}$ $y = \dfrac{3}{x}$

21.

Answer.

A vertical compression, the scale factor is $\dfrac{1}{2}\text{:}$ $y = \dfrac{1}{2}x^3$

23.

Answer.

Scale factor $\frac{1}{3} \text{;}$ $y =\abs{x}$ is compressed vertically by the scale factor.

25.

Answer.

Scale factor $-2 \text{;}$ $y =\frac{1}{z^2}$ is reflected over the $z$-axis and stretched vertically by a factor of $2\text{.}$

27.

Answer.

Scale factor $-3 \text{;}$ $y =\sqrt{v}$ is reflected over the $v$-axis and stretched vertically by a factor of $3\text{.}$

29.

Answer.

Scale factor $\frac{-1}{2} \text{;}$ $y =s^3 $ is reflected over the $s$-axis and compressed vertically by a factor of $\frac{1}{2}\text{.}$

31.

Answer.

Scale factor $\frac{1}{3} \text{;}$ $y =\frac{1}{x} $ is compressed vertically by the scale factor.

33.

Answer.

35.

Answer.

Vertical stretch by a factor of $3\text{:}$ $y = 3 f (x)$
Reflection about the $x$-axis: $y = -f (x)$
Translation $1$ unit right: $y = f (x - 1)$
Translation $4$ units up: $y = f (x) + 4$

37.

Answer.

Reflection about the $v$-axis and vertical stretch by a factor of $2\text{:}$ $T = -2h(v)$
Vertical stretch by a factor of $3\text{:}$ $T = 3h(v)$
Translation $3$ units up: $T = h(v) + 3$
Translation $3$ units left: $T = h(v + 3)$

39.

Answer.

Translation $2$ units up: $y = f (x) + 2$
Translation $4$ units down: $y = f (x) - 4$
Vertical compression by a factor of $\frac{1}{2} \text{:}$ $y = \frac{1}{2}f (x)$
Translation $1$ unit right: $y = f (x - 1)$

41.

Answer.

Translation $1$ unit right: $y = f (x - 1)$
Part (a) is translated $30$ units up: $y = f (x - 1) + 30$
$f$ is reflected about the $x$-axis and stretched vertically by a factor of $2\text{:}$ $y = -2 f (x)$
Part (c) is translated $10$ units down: $y = -2 f (x) - 10$

43.

Answer.

$y = \dfrac{1}{2}\cdot\dfrac{1}{x^2}$ is a vertical compression with factor $dfrac{1}{2} $ of $y = \dfrac{1}{x^2}\text{.}$

45.

Answer.

$y = 2\sqrt[3]{x}$ is a vertical stretch with factor $2 $ of $y = \sqrt[3]{x}\text{.}$

47.

Answer.

$y = 3\abs{x}$ is a vertical stretch with factor $3 $ of $y = \abs{x}\text{.}$

49.

Answer.

$y = \dfrac{1}{8}x^3 $ is a vertical compression with factor $\dfrac{1}{8} $ of $y = x^3\text{.}$

51.

Answer.

Translation by $2$ units up and $3$ units right

53.

Answer.

Translation by $2$ units left and $3$ units down.

55.

Answer.

Reflection across the $u$-axis, vertical stretch by a factor of $3\text{,}$ translation by $4$ units left and $4$ units up

57.

Answer.

Vertical stretch by a factor of $2\text{,}$ translation by $5$ units right and $1$ down

59.

Answer.

Reflection across the $w$-axis, vertical stretch by a factor of $2\text{,}$ translation by $6$ units up and $1$ unit right

61.

Answer.

Translation by $8$ units right and $1$ unit down

63.

Answer.

Translation by $4$ units up and $1$ unit right: $y = f (x - 1) + 4$
Vertical stretch by a factor of $2$ and a translation by $4$ units up: $y = 2 f (x) + 4$

65.

Answer.

$y =\abs{x}$ translated by $1$ unit left and $2$ units down
$\displaystyle y =\abs{x+1} - 2$

67.

Answer.

$y =\sqrt{x}$ reflected about the $x$-axis and shifted $3$ units up
$\displaystyle y =-\sqrt{x} +3$

69.

Answer.

$y =x^3$ translated by $3$ units right and $1$ unit up
$\displaystyle y =(x - 3)^3 + 1$

71.

Answer.

$y = f(x - 20)\text{:}$ Students scored $20$ points higher than Professor Hilbert’s class.
$y = 1.5 f(x)\text{:}$ The class is about $50\%$ larger than Hilbert’s, but the classes scored the same.

73.

Answer.

$y = f (x - 5000)\text{:}$ Taxpayers earn $$5000$ more than Californians in each tax rate
$y = f (x) - 0.2\text{:}$ Taxpayers pay $0.2\%$ less tax than Californians on the same income.

75.

Answer.

$y = g(t + 2)\text{:}$ This population has its maximum and minimum two months before the marmots.
$y = g(t) - 20\text{:}$ This population remains $20$ fewer than that of the marmots.

2.4 Functions as Mathematical Models
Homework 2.4

1.

Answer.

(b)

3.

Answer.

(a)

5.

Answer.

7.

Answer.

9.

Answer.

(b)

11.

Answer.

13.

Answer.

15.

Answer.

17.

Answer.

19.

Answer.

$y = x^3$ stretched or compressed vertically

21.

Answer.

$y =\dfrac{1}{x} $ stretched or compressed vertically

23.

Answer.

$y =\sqrt{x} $

25.

Answer.

Increasing
Concave up

27.

Answer.

Increasing
Concave down

29.

Answer.

Increasing, linear (neither concave up nor down)
C

31.

Answer.

Increasing, concave down
F

33.

Answer.

Decreasing, linear (neither concave up nor down)
D

35.

Answer.

$y=4 \sqrt[3]{x} $

37.

Answer.

$y=3\cdot \dfrac{1}{x^2} $

39.

Answer.

$y=0.5 x^2 $

41.

Answer.

Table (4), Graph (C)
Table (3), Graph (B)
Table (1), Graph (D)
Table (2), Graph (A)

43.

Answer.

45.

Answer.

$\displaystyle S(x) = \begin{cases} 5.95 \amp x \le 25\\ 7.95 \amp 25\lt x\le 50\\ 9.95 \amp 50\lt x\le 75\\ 10.95 \amp 75\lt x\le 100 \end{cases}$

47.

Answer.

During the first 400 seconds Bob’s altitude is climbing with the aircraft; then the aircraft maintains a constant altitude of 10,000 feet for the next 100 seconds; after jumping from the plane, Bob falls for 20 seconds before opening the parachute; he falls at a constant rate after the chute opens.
$240$ seconds (4 minutes) and $500 + \sqrt{250}\approx 515.8$

49.

Answer.

$m\approx 3.2$ mm/cc: The height of precipitate increases by $1$ mm for each additional cc of lead nitrate
$\displaystyle f(x)= \begin{cases} 1.34 + 3.2x \amp x \lt 2.6\\ 9.6 \amp x\ge 2.6 \end{cases}$
The increasing portion of the graph corresponds to the period when the reaction was occurring, and the horizontal section corresponds to when the potassium iodide is used up.

51.

Answer.

2.5 The Absolute Value Function
Homework 2.5

1.

Answer.

$\displaystyle \abs{x}=6 $

3.

Answer.

$\displaystyle \abs{p+3}=5 $

5.

Answer.

$\displaystyle \abs{t-6}\lt 3 $

7.

Answer.

$\displaystyle \abs{b+1}\ge 0.5 $

9.

Answer.

$x = -5$ or $x = -1$
$\displaystyle -7\le x\le 1$
$x\lt -8$ or $x\gt 2$

11.

Answer.

$\displaystyle x = 4$
No solution
No solution

13.

Answer.

$x=\dfrac{-3}{2} $ or $x=\dfrac{5}{2} $

15.

Answer.

$q=\dfrac{-7}{3} $

17.

Answer.

$b=-14 $ or $b=10 $

19.

Answer.

$w=\dfrac{13}{2} $ or $w=\dfrac{15}{2} $

21.

Answer.

No solution

23.

Answer.

No solution

25.

Answer.

$\dfrac{-9}{2}\lt x \lt \dfrac{-3}{2} $

27.

Answer.

$d\le -2~ $ or $~ d\ge 5 $

29.

Answer.

All real numbers

31.

Answer.

$1.4 \lt t\lt 1.6 $

33.

Answer.

$T\le 3.2~$ or $~T\ge 3.3 $

35.

Answer.

No solution

37.

Answer.

$4.299\lt l\lt 4.301$

39.

Answer.

$250\le t\le 350$

41.

Answer.

$\abs{T - 5}\lt 0.3$

43.

Answer.

$\abs{D-100}\le 5$

45.

Answer.

$\abs{g-0.25}\le 0.001$

47.

Answer.

$\abs{t - 200}\lt 50\text{,}$ $~150\le t\lt 250$
$\abs{t - 200}\lt 0.5\text{,}$ $~199.5\le t\lt 200.5$
$\abs{t - 200}\lt 0.05\text{,}$ $~199.95\le t\lt 200.05$

49.

Answer.

$\displaystyle \abs{3x-6} = \begin{cases} -(3x-6) \amp \text{if } x\lt 2 \\ 3x-6 \amp \text{if } x\ge 2 \end{cases}$
$-(3x - 6)\le 9\text{,}$ $~3x - 6\lt 9$
$\displaystyle -1\lt x\lt 5$
The solutions are the same.

51.

Answer.

$\displaystyle \abs{2x+5} = \begin{cases} -(2x+5) \amp \text{if } x\lt \dfrac{-5}{2} \\ 2x+5 \amp \text{if } x\ge \dfrac{-5}{2} \end{cases}$
$-(2x+5)\gt 7\text{,}$ $~2x+5\gt 7$
$x\lt -6$ or $~x\gt 1$
The solutions are the same.

53.

Answer.

$\displaystyle f(x) = \begin{cases} -2x, \amp x\lt -4 \\ 8, \amp -4\le x\le 4 \\ 2x, \amp x\gt 4 \end{cases} $
The graphs looks like like a trough. The middle horizontal section is $y = p + q$ for $-p \le x\le q\text{,}$ the left side, $x\lt -p\text{,}$ has slope $-2$ and the right side, $x\gt q\text{,}$ has slope $2\text{.}$
$\displaystyle g(x) = \begin{cases} -2x+q-p, \amp x\lt -p \\ p+q, \amp -p\le x\le q \\ 2x+p-q, \amp x\gt q \end{cases} $

55.

Answer.

$\displaystyle f(x) = \begin{cases} -3x, \amp x\lt -4 \\ -x+8, \amp -4\le x\le 0 \\ x+8, \amp 0\lt x\lt 4 \\ 3x, \amp x\ge 4 \end{cases} $
$\displaystyle 8$
$\displaystyle p+q$

57.

Answer.

$\abs{x + 12}\text{,}$ $\abs{x + 4}\text{,}$ $\abs{x - 24}$
$\displaystyle f(x)=\abs{x + 12}+\abs{x + 4}+\abs{x - 24}$
At $x$-coordinate $-4$

59.

Answer.

$2$ miles east of the river

2.6 Domain and Range
Homework 2.6

1.

Answer.

Domain: $[-5, 3]\text{;}$ Range: $[-3, 7]$

3.

Answer.

Domain: $[-4,5]\text{;}$ Range: $[-1, 1) \cup [3, 6]$

5.

Answer.

Domain: $[-2,2]\text{;}$ Range: $[-1,1]$

7.

Answer.

Domain: $(-5,5]\text{;}$ Range: $\{-1,0,2,3\}$

9.

Answer.

Domain: all real numbers; Range: all real numbers
Domain: all real numbers; Range: $[0, \infty)$

11.

Answer.

Domain: all real numbers except zero; Range: $(0, \infty)$
Domain: all real numbers except zero; Range: all real numbers except zero

13.

Answer.

Domain: $[0, 26.2]\text{;}$ Range: $[90, 300]$

15.

Answer.

Domain: $[0, 600]\text{;}$ Range: $[-90, 700]$

17.

Answer.

$\displaystyle V(t) = 6000 - 550t$
Domain: $[0, 10]\text{;}$ Range: $[500, 6000]$

19.

Answer.

Domain: $[0, 4]\text{;}$ Range: $[0, 64].~~$The ball reaches a height of 64 feet and hits the ground 4 seconds after being hit.

21.

Answer.

Range: $\{2.50, 2.90, 3.30, 3.70, 4.10\}$
$$13.30$

23.

Answer.

Domain: nonnegative integers; The range includes all whole number multiples of $2.50$ up to $20\times 2.50 = 50\text{,}$ all integer multiples of $2.25$ from $21\times 2.25 = 47.25$ to $50 \times 2.25 = 112.50$ and all integer multiples of $2.10$ from $51\times 2.10 = 107.10$ onwards: $0, 2.50, 5.00, 7.50, \ldots, 50\text{,}$ $47.25, 49.50, 51.75, \ldots , 112.50\text{,}$ $107.10, 109.20, 111.30, \ldots$

25.

Answer.

$f (x)$ domain: $x \ne 4\text{;}$ Range: $(0,\infty)$
$h (x)$ domain: $x \ne 0\text{;}$ Range: $(-4,\infty)$

27.

Answer.

$G(v)$ domain: all real numbers; Range: all real numbers
$H(v)$ domain: all real numbers; Range: all real numbers

29.

Answer.

$G(v)$ domain: $[2,\infty)\text{;}$ Range: $[0,\infty)$
$H(v)$ domain: $[0,\infty)\text{;}$ Range: $[-2,\infty)$

31.

Answer.

Not in range
$x = -6$ or $x = 2$

33.

Answer.

$\displaystyle t = -64$
$\displaystyle t=-8$

35.

Answer.

$\displaystyle w=\dfrac{1}{2} $
Not in range

37.

Answer.

Not in range
$\displaystyle h=4$

39.

Answer.

Domain: $[-2, 5]\text{;}$ Range: $[-4, 12]$

41.

Answer.

Domain: $[-5, 3]\text{;}$ Range: $[-15, 1]$

43.

Answer.

Domain: $[-2, 2]\text{;}$ Range: $[-9, 7]$

45.

Answer.

Domain: $[-1, 8]\text{;}$ Range: $[0, 3]$

47.

Answer.

Domain: $[-1.25, 2.75]\text{;}$ Range: $\left[\dfrac{4}{17} , 4\right]$

49.

Answer.

Domain: $(3, 6]\text{;}$ Range: $\left[-\infty,\dfrac{-1}{3} \right]$

51.

Answer.

Squaring both sides of the equation gives the equation of the circle centered on the origin with radius $4\text{,}$ but the points in the third and fourth quadrants are extraneous solutions introduced by squaring. (The original equation allowed only $y\ge 0\text{.}$)
Domain: $[-4, 4]\text{;}$ Range: $[0, 4]$
The calculator does not show the graph extending down to the $x$-axis.

53.

Answer.

Domain: $x \ne 2\text{;}$ Range: $(0, \infty)$
Domain: $x \ne 0\text{;}$ Range: $(-2, \infty)$
Domain: $x \ne 3\text{;}$ Range: $(-5, \infty)$

55.

Answer.

Domain: all real numbers; Range: $(-\infty,0)$
Domain: all real numbers; Range: $(-\infty,6]$
Domain: all real numbers; Range: $(-\infty,6]$

57.

Answer.

Domain: $[3,13]\text{;}$ Range: $[-2,2]$
Domain: $[0,10]\text{;}$ Range: $[-6,6]$
Domain: $[5,15]\text{;}$ Range: $[-4,4]$

59.

Answer.

Domain: $(0,\infty)\text{;}$ Range: $(0,5)$
Domain: $(-2,\infty)\text{;}$ Range: $(0,3)$
Domain: $(3,\infty)\text{;}$ Range: $(2,4)$

61.

Answer.

$\displaystyle f(x)$
$\displaystyle g(x) $

63.

Answer.

$\displaystyle g(x)$
$\displaystyle f(x) $

65.

Answer.

Domain: $[0\degree , 90\degree]\text{;}$ Range: $[12 , 24]$

2.7 Chapter Summary and Review
Chapter 2 Review Problems

1.

Answer.

$x = 1$ or $x = 4$

3.

Answer.

$w = -2$ or $w = 4$

5.

Answer.

$r = -1 \pm \sqrt{\dfrac{A}{P}}$

7.

Answer.

$11\%$

9.

Answer.

$P = 1.001$

11.

Answer.

$m = 29$

13.

Answer.

$r = 3$

15.

Answer.

$\sqrt{12,132}\approx 110$ cm

17.

Answer.

$-2$

19.

Answer.

$24$

21.

Answer.

$x = -2$ or $x = 6$
$\displaystyle (-2, 6)$
$\displaystyle (-\infty,-2] \cup [6,+\infty)$

23.

Answer.

$x = 0$ or $x = 3$
$\displaystyle (-\infty,0) \cup (3,\infty)$
$\displaystyle (0, 3)$

25.

Answer.

27.

Answer.

29.

Answer.

31.

Answer.

$y =\abs{x}$ shifted up $2$ units

33.

Answer.

$y =\sqrt{x}$ shifted up $3$ units

35.

Answer.

$y =\abs{x}$ shifted left $2$ units and down $3$ units

37.

Answer.

$y =\sqrt{x}$ reflected across the horizontal axis and stretched vertically by a factor of $2$

39.

Answer.

$\displaystyle y =\dfrac{-3}{2}f (t)$
$\displaystyle y =\dfrac{-3}{2}f (t)+3$
$\displaystyle y =\dfrac{-3}{2}f (t+2)+3$

41.

Answer.

$\displaystyle y = f (t - 1)$
$\displaystyle y = -f (t - 1)$
$\displaystyle y = -f (t - 1)+300$

43.

Answer.

$y = (x - 2)^2 - 4$

45.

Answer.

47.

Answer.

I (c), II (b), III (a)

49.

Answer.

$g(t) = \begin{cases} 60+t, \amp 0\le t \lt 10\\ 70, \amp 10\le t \lt 30\\ 70 - \frac{1}{2}(t - 30), \amp 30\le t \le 60 \end{cases}$

51.

Answer.

$\abs{x}=4 $

53.

Answer.

$\abs{p-7}\lt 4 $

55.

Answer.

$t = \dfrac{6}{5}$ or $t = \dfrac{12}{5}$

57.

Answer.

No solutions

59.

Answer.

$p = 1$ or $p = 6$

61.

Answer.

$\left(\dfrac{-2}{3}, 2\right)$

63.

Answer.

$(-\infty,-0.9] \cup [0.1,\infty)$

65.

Answer.

$\abs{H - 65.5}\lt 9.5$

67.

Answer.

$[2.05, 2.15]$

69.

Answer.

$\displaystyle g(x)=\dfrac{24}{x} $

71.

Answer.

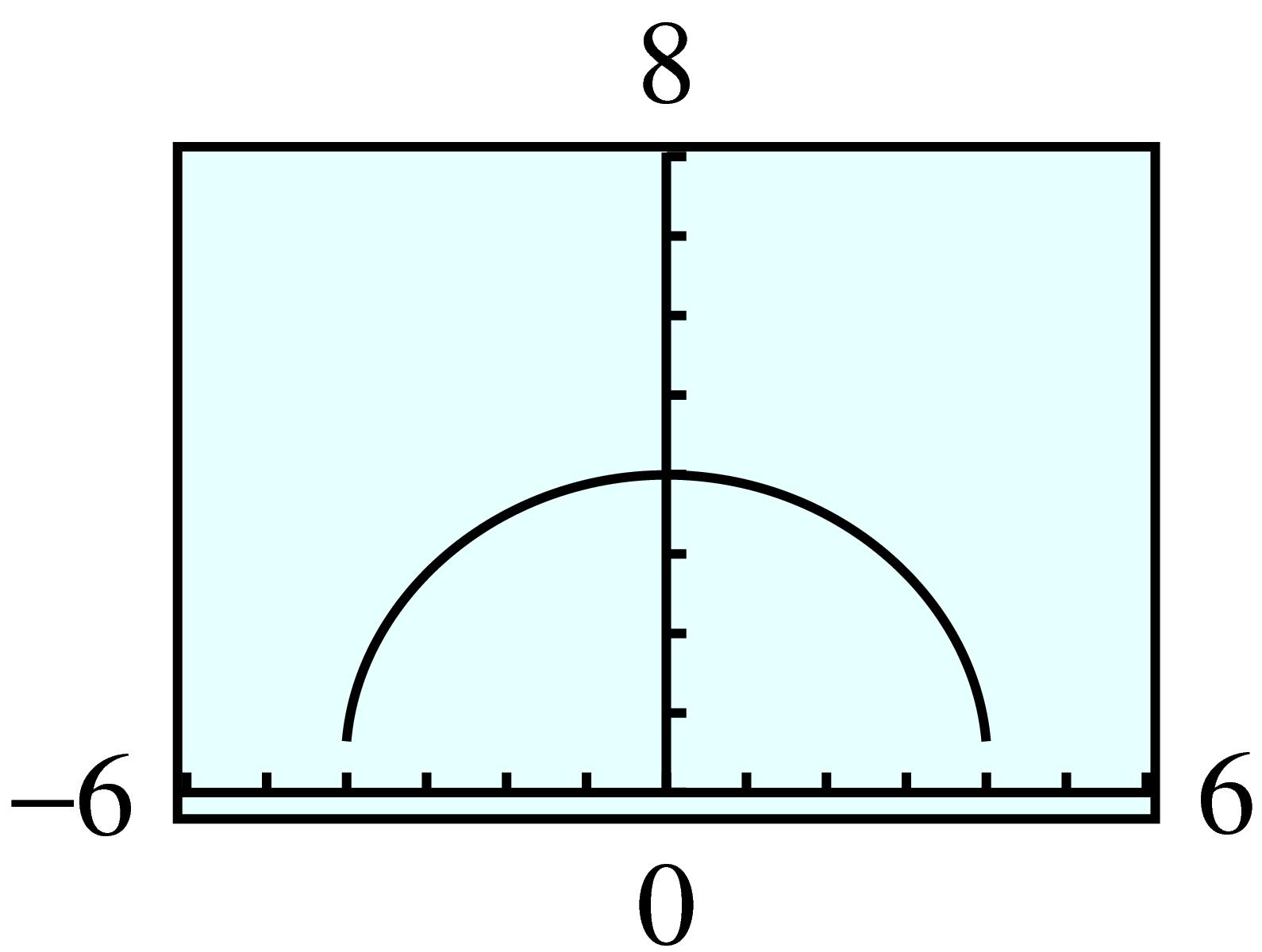
$x$ $0$ $4$ $8$ $14$ $16$ $22$

$y$ $24$ $20$ $16$ $10$ $8$ $2$
$\displaystyle y = 24 - x$

73.

Answer.

$x$ $0$ $1$ $4$ $9$ $16$ $25$

$y$ $0$ $1$ $2$ $3$ $4$ $5$
$\displaystyle y = \sqrt{x} $

75.

Answer.

$x$ $-3$ $-2$ $-1$ $0$ $1$ $2$

$y$ $5$ $0$ $-3$ $-4$ $-3$ $0$
$\displaystyle y = x^2-4 $

77.

Answer.

Domain: $[-2, 4]\text{;}$ Range: $[-10, -4]$

79.

Answer.

Domain: $(-2, 4]\text{;}$ Range: $\left[\dfrac{1}{6} , \infty\right)$

3 Power Functions
3.1 Variation
Homework 3.1

1.

Answer.

$\text{Price of item} $ $18$ $28$ $12$

$\text{Tax} $ $1.17$ $1.82$ $0.78$

$\text{Tax}/\text{Price} $ $\alert{0.065}$ $\alert{0.065}$ $\alert{0.065}$

Yes; $6.5\%$
$\displaystyle T = 0.065p$

3.

Answer.

$\text{Width (feet)} $ $2$ $2.5$ $3$

$\text{Length (feet)} $ $12$ $9.6$ $8$

$\text{Length}\times \text{width} $ $\alert{24}$ $\alert{24}$ $\alert{24}$

$24$ square feet
$\displaystyle L = \dfrac{24}{w} $

5.

Answer.

The ratio $\dfrac{y}{x} $ is a constant.
The product $xy$ is a constant.

7.

Answer.

Length	Width	Perimeter	Area
$10$	$8$	$\alert{36} $	$\alert{80} $
$12$	$8$	$\alert{40} $	$\alert{96} $
$15$	$8$	$\alert{46} $	$\alert{120} $
$20$	$8$	$\alert{56} $	$\alert{160} $

No
$\displaystyle P=16+2l$
Yes
$\displaystyle A=8l$

9.

Answer.

(b)

11.

Answer.

(c)

13.

Answer.

$\displaystyle m = 0.165w$

$w$ $50$ $100$ $200$ $400$

$m$ $\alert{8.25}$ $\alert{16.5}$ $\alert{33}$ $\alert{66}$
$19.8$ lb
$303.03$ lb
It will double.

15.

Answer.

$\displaystyle L = 0.8125T^2$

$T$ $1$ $5$ $10$ $20$

$L$ $\alert{0.8125} $ $\alert{20.3} $ $\alert{81.25} $ $\alert{325} $
$234.8125$ ft
$0.96$ sec
It must be four times as long.

17.

Answer.

$\displaystyle B = \dfrac{88}{d}$

$d$ $1$ $2$ $12$ $24$

$B$ $\alert{88} $ $\alert{44} $ $\alert{7.3} $ $\alert{3.7} $
$8.8$ milligauss
More than $20.47$ in
It is one half as strong.

19.

Answer.

$\displaystyle P = \dfrac{1825}{8192}w^3\approx0.228w^3$

$w$ $10$ $20$ $40$ $80$

$P$ $\alert{223} $ $\alert{1782} $ $\alert{14,259} $ $\alert{114,074} $
$752$ kilowatts
$33.54$ mph
It is multiplied by $8\text{.}$

21.

Answer.

$\displaystyle y= 0.3x$
$x$ $y$

$2$ $\alert{0.6}$

$5$ $1.5$

$\alert{8}$ $2.4$

$12$ $\alert{3.6} $

$\alert{15} $ $4.5$
$y$ doubles.

23.

Answer.

$\displaystyle y= \dfrac{2}{3} x^2$
$x$ $y$

$3$ $\alert{6}$

$6$ $24$

$\alert{9}$ $54$

$12$ $\alert{96} $

$\alert{15} $ $150$
$y$ is quadrupled.

25.

Answer.

$\displaystyle y= \dfrac{120}{x} $
$4$ $\alert{30}$

$\alert{8} $ $15$

$20$ $6$

$30$ $\alert{4} $

$\alert{40} $ $3$
$y$ is halved.

27.

Answer.

(b) $y = 0.5x^2$

29.

Answer.

31.

Answer.

(b) $y =\dfrac{72}{x^2}$

33.

Answer.

35.

Answer.

$\displaystyle d = 0.005v^2$
$50$ m

37.

Answer.

$\displaystyle m =\dfrac{8}{p} $
$0.8$ ton

39.

Answer.

$\displaystyle T=\dfrac{6}{d} $
$1\degree$C

41.

Answer.

$\displaystyle W = 600d^2 $
$864$ newtons

43.

Answer.

Wind resistance quadruples.
It is one-ninth as great.
It is decreased by $19\%$ because it is $81\%$ of the original.

45.

Answer.

It is one-fourth the original illumination.
It is one-ninth the illumination.
It is $64\%$ of the illumination.

47.

Answer.

$\displaystyle D = (2.5\times 10^{-52})m^2$
$2\times 10^{74}$ kg
$\displaystyle 1.7\times 10^{-8} ~m$

49.

Answer.

$\displaystyle L = (1.25\times 10{-27})m^3$
$2\times 10^{12}$ kg

51.

Answer.

$y = kx$ implies that $k(cx)=c(kx)=cy\text{.}$

53.

Answer.

If $y = kx^2\text{,}$ then dividing both sides of the equation by $x^2$ gives $\dfrac{y}{x^2} = k\text{.}$

55.

Answer.

Yes

3.2 Integer Exponents
Homework 3.2

1.

Answer.

$n$	$-5$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$	$5$
$3^n$	$\frac{1}{243} $	$\frac{1}{81} $	$\frac{1}{27} $	$\frac{1}{9} $	$\frac{1}{3} $	$1$	$3$	$9$	$27$	$81$	$243$

Each time $n$ increases by $1\text{,}$ we multiply the power in the bottom row by $3\text{.}$

3.

Answer.

$\displaystyle 8$
$\displaystyle -8$
$\displaystyle \dfrac{1}{8} $
$\displaystyle \dfrac{-1}{8} $

5.

Answer.

$\displaystyle \dfrac{1}{8} $
$\displaystyle \dfrac{-1}{8} $
$\displaystyle 8 $
$\displaystyle -8 $

7.

Answer.

$\displaystyle \dfrac{1}{2^1}=\dfrac{1}{2} $
$\displaystyle \dfrac{1}{(-5)^2}=\dfrac{1}{25} $
$\displaystyle 3^3=27 $
$\displaystyle (-2)^4=16 $

9.

Answer.

$\displaystyle 5\cdot 4^3=320 $
$\displaystyle \dfrac{1}{(2q)^5}=\dfrac{1}{32q^5} $
$\displaystyle \dfrac{-4}{x^2} $
$\displaystyle 8b^3 $

11.

Answer.

$\displaystyle \dfrac{1}{(m-n)^2} $
$\displaystyle \dfrac{1}{y^2}+\dfrac{1}{y^3} $
$\displaystyle \dfrac{2p}{q^4} $
$\displaystyle \dfrac{-5x^{5}}{y^{2}} $

13.

Answer.

$x$ $1$ $2$ $4$ $8$ $16$

$x^{-2}$ $1 $ $0.25 $ $0.06 $ $0.02 $ $0.00 $
The values of $f (x)$ decrease, because $x^{-2}$ is the reciprocal of $x^2\text{.}$
$x$ $1$ $0.5$ $0.25$ $0.125$ $0.0625$

$x^{-2}$ $1 $ $4 $ $16 $ $64 $ $256 $
The values of $f (x)$ increase toward infinity, because $x^{-2}$ is the reciprocal of $x^2\text{.}$

15.

Answer.

b. (ii), (iii), and (iv) have the same graph, because they represent the same function.

17.

Answer.

$\displaystyle F(r)=3r^{-4} $
$\displaystyle G(w)=\dfrac{2}{5}w^{-3} $
$\displaystyle H(z)=\dfrac{1}{9}z^{-2} $

19.

Answer.

$x=-1.25$ or $x=1.25$

21.

Answer.

$t=\dfrac{1}{16} $

23.

Answer.

$v=\dfrac{1}{5} $ or $v=\dfrac{-1}{5}$

25.

Answer.

$\displaystyle P = 0.355v^3$
$v\approx 52.03$ mph
$\displaystyle 3.375$

27.

Answer.

$\displaystyle D =\dfrac{70}{i} $
It decreases by about $2.3$ years.

29.

Answer.

$\displaystyle L = \left(4\pi sR^2 \right)T^4\approx 7.2\times 10^{-7}R^2T^4$
$4840$ K

31.

Answer.

$500$ picowatts
$\displaystyle P = 8000d^{-4}$
$d$ (nautical miles) $4$ $5$ $7$ $10$

$P$ (picowatts) $31.3 $ $12.8$ $3.3$ $0.8$
$16.8$ nautical miles

33.

Answer.

$\displaystyle T = 16kr^2$
$\displaystyle T = 0.1r^2$

35.

Answer.

$\displaystyle a^5$
$\displaystyle \dfrac{1}{5^7} $
$\displaystyle \dfrac{1}{p^3} $
$\displaystyle \dfrac{1}{7^{10}} $

37.

Answer.

$\displaystyle \dfrac{20}{x^3} $
$\displaystyle \dfrac{1}{3u^{12}} $
$\displaystyle 5^8 t $

39.

Answer.

$\displaystyle \dfrac{x^4}{9y^6} $
$\displaystyle \dfrac{a^6 b^4}{36} $
$\displaystyle \dfrac{5}{6h^6} $

41.

Answer.

$\displaystyle \dfrac{1}{3}x+3x^{-1} $
$\displaystyle \dfrac{1}{4}x^{-2}-\dfrac{3}{2}x^{-1} $

43.

Answer.

$\displaystyle \dfrac{1}{2}x^{-2}+x^{-3}-\dfrac{1}{2}x^{-4} $
$\displaystyle \dfrac{2}{3}x^{-2}-\dfrac{1}{9}+\dfrac{1}{6}x^{2} $

45.

Answer.

$x - 3 + 2x^{-1}$

47.

Answer.

$-3 + 6t^{-2} + 12t^{-4}$

49.

Answer.

$-4 - 2u^{-1} + 6u^{-2}$

51.

Answer.

$4x^{-2}(x^4 + 4)$

53.

Answer.

$a^{-3}(3 - 3a^4 + a^6)$

55.

Answer.

No, because $\frac{1}{(x+y)^2}$ is not $\frac{1}{x^2} + \frac{1}{y^2}\text{.}$
Let $x = 1\text{,}$ $y = 2\text{,}$ then $(x + y)^{-2} = (1 + 2)^{-2} = 3^{-2} = \frac{1}{9}\text{,}$ but $x^{-2} + y^{-2} = 1^{-2} + 2^{-2} = 1 + \frac{1}{4} = \frac{5}{4}$

57.

Answer.

$\displaystyle x + x^{-1} = x + \dfrac{1}{x} = \dfrac{x^2}{x}+\dfrac{1}{x}= \dfrac{x^2 + 1}{x}$
$\displaystyle x^3 + x^{-3} = x^3 + \dfrac{1}{x^3} = \dfrac{x^6}{x^3}+\dfrac{1}{x^3}= \dfrac{x^6 + 1}{x^3}$
$\displaystyle x^n + x^{-n} = x^n + \dfrac{1}{x^n} = \dfrac{x^{2n}}{x^n}+\dfrac{1}{x^n}= \dfrac{x^{2n} + 1}{x^2}$

59.

Answer.

\begin{align*} a^{-2}a^{-3} \amp= \frac{1}{a^2}\cdot\frac{1}{a^3}=\frac{1}{a^2\cdot a^3} \\ \amp= \frac{1}{a^{2+3}} \amp\amp \text{By the first law of exponents.} \\ \amp= \frac{1}{a^5}=a^{-5} \end{align*}

61.

Answer.

\begin{align*} \frac{a^{-2}}{a^{-6}} \amp= a^{-2}\div a^{-6} = \frac{1}{a^2}\div\frac{1}{a^6} \\ \amp= \frac{1}{a^{2}}\cdot\frac{a^6}{1} = \frac{a^6}{a^2} \\ \amp= a^{6-2}\amp\amp \text{By the second law of exponents.} \\ \amp= a^4 \end{align*}

3.3 Roots and Radicals
Homework 3.3

1.

Answer.

$\displaystyle 11$
$\displaystyle 3$
$\displaystyle 5$

3.

Answer.

$\displaystyle 2$
$\displaystyle 2$
$\displaystyle 9$

5.

Answer.

$\displaystyle 3$
$\displaystyle 3$
$\displaystyle 2 $

7.

Answer.

$\displaystyle 2$
$\displaystyle \dfrac{1}{2} $
$\displaystyle \dfrac{1}{8} $

9.

Answer.

$\displaystyle \sqrt{3} $
$\displaystyle 4\sqrt[3]{x} $
$\displaystyle \sqrt[5]{4x} $

11.

Answer.

$\displaystyle \dfrac{1}{\sqrt[3]{6}} $
$\displaystyle \dfrac{3}{\sqrt[8]{xy}} $
$\displaystyle \sqrt[4]{x-2} $

13.

Answer.

$\displaystyle 7^{1/2} $
$\displaystyle (2x)^{1/3} $
$\displaystyle 2z^{1/5} $

15.

Answer.

$\displaystyle -3\cdot 6^{-1/4} $
$\displaystyle (x-3y)^{1/4} $
$\displaystyle -(1+3b)^{-1/5} $

17.

Answer.

$\displaystyle 125$
$\displaystyle 2$
$\displaystyle 63$
$\displaystyle -2x^7$

19.

Answer.

$\displaystyle 1.414$
$\displaystyle 4.217$
$\displaystyle 1.125$
$\displaystyle 0.140$
$\displaystyle 2.782 $

21.

Answer.

$\displaystyle g(x) = 3.7x^{1/3} $
$\displaystyle H(x) = 85^{1/4}x^{1/4} $
$\displaystyle F(t) = 25t^{-1/5} $

23.

Answer.

$x = 91.125$

25.

Answer.

$x = 241$

27.

Answer.

$x = \dfrac{19}{2} $

29.

Answer.

$x = \pm\sqrt{30} $

31.

Answer.

$L=\dfrac{gT^2}{4\pi^2} $

33.

Answer.

$s=\pm\sqrt{t^2-r^2} $

35.

Answer.

$v=\dfrac{4}{3}\pi r^3 $

37.

Answer.

$p=\dfrac{8Lvf}{\pi R^4} $

39.

Answer.

$\displaystyle T=\dfrac{2\pi}{\sqrt{32}}L^{1/2} $
$90$ feet

41.

Answer.

$3$ meters per second
$\approx 2.2$ meters per second
$1.9$ meters
$1.2$ meters per second

43.

Answer.

$6.5\times 10^{-13}$ cm; $1.17\times 10^{-36} \text{ cm}^3$
$\displaystyle 1.8\times 10^{14} g/\text{cm}^3$
Element Carbon Potassium Cobalt Technetium Radium

Mass
number, $A$ $14$ $40$ $60$ $99$ $226$

Radius, $r$
($10^{-13}$ cm) $3.1$ $4.4$ $5.1$ $6$ $7.9$

45.

Answer.

$\displaystyle s = 50\sqrt{d}$
$30$ cm/sec

47.

Answer.

$\displaystyle r = 12.1\sqrt{P}$
$94$ ft/sec

49.

Answer.

$287\text{;}$ $343$
$2015\text{;}$ $2058$
The membership grows rapidly at first but is growing less rapidly with time.

51.

Answer.

I
III
II
none

53.

Answer.

The graphs of $x^{1/n}$ become closer and closer to horizontal when $n$ increases (for $x\gt 1$).
$\displaystyle 10,~ 4.64,~ 3.16,~ 2.51$
$1.58, 1.05,~ 1.005\text{;}$ the values decrease towards $1\text{.}$

55.

Answer.

The graphs of $y_1$ and $y_2$ are symmetric about $y_3 = x\text{.}$

57.

Answer.

The graphs of $y_1$ and $y_2$ are symmetric about $y_3 = x\text{.}$

59.

Answer.

$\displaystyle x=36$

61.

Answer.

$\displaystyle x^{1/2}$
$\displaystyle \left(x^{1/2} \right)^{1/2} $
\begin{equation*} \begin{aligned}[t] \sqrt{\sqrt{x}}\amp =\left(x^{1/2} \right)^{1/2} \amp\amp\text{By definition of fractional exponents.}\\ \amp=x^{1/4} \amp\amp\text{By the third law of exponents.}\\ \amp=\sqrt[4]{x} \amp\amp\text{By definition of fractional exponents.} \end{aligned} \end{equation*}

63.

Answer.

$\displaystyle{\frac{1}{4}x^{1/2}-2x^{-1/2}+\frac{1}{\sqrt{2}}x}$

65.

Answer.

$\displaystyle{3x^{-1/3}-\frac{1}{2}}$

67.

Answer.

$x^{0.5} + x^{-0.25} - x^0$

3.4 Rational Exponents
Homework 3.4

1.

Answer.

$\displaystyle 27$
$\displaystyle 25$
$\displaystyle 125$

3.

Answer.

$\displaystyle \dfrac{1}{64} $
$\displaystyle \dfrac{1}{16} $
$\displaystyle \dfrac{1}{256} $

5.

Answer.

$\displaystyle \sqrt[5]{x^4} $
$\displaystyle \dfrac{1}{\sqrt[6]{b^5} } $
$\displaystyle \dfrac{1}{\sqrt[3]{(pq)^2}} $

7.

Answer.

$\displaystyle 3\sqrt[5]{x^2} $
$\displaystyle \dfrac{4}{\sqrt[3]{z^4}} $
$\displaystyle -2\sqrt[4]{xy^3} $

9.

Answer.

$\displaystyle x^{2/3} $
$\displaystyle 2a^{1/5}b^{3/5} $
$\displaystyle -4m p^{-7/6} $

11.

Answer.

$\displaystyle (ab)^{2/3} $
$\displaystyle 8x^{-3/4} $
$\displaystyle \dfrac{1}{3}RT^{-1/2}K^{-5/2} $

13.

Answer.

$\displaystyle 8 $
$\displaystyle -81 $
$\displaystyle 2y^3 $

15.

Answer.

$\displaystyle -a^4 b^8 $
$\displaystyle 2x^3y^9 $
$\displaystyle -3a^2 b^3 $

17.

Answer.

$\displaystyle 7.931$
$\displaystyle 10.903$
$\displaystyle 0.090$
$\displaystyle 35.142$

19.

Answer.

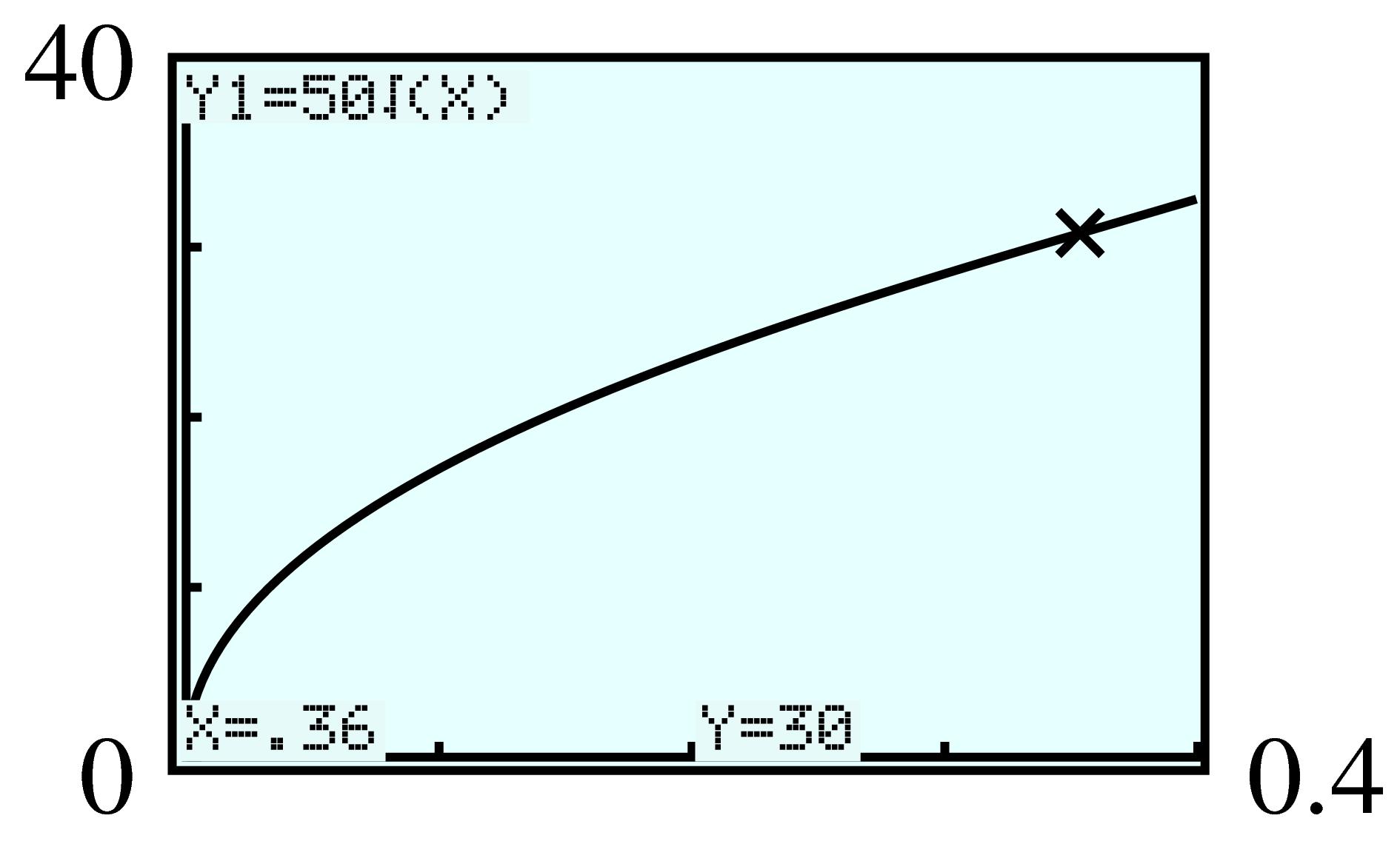
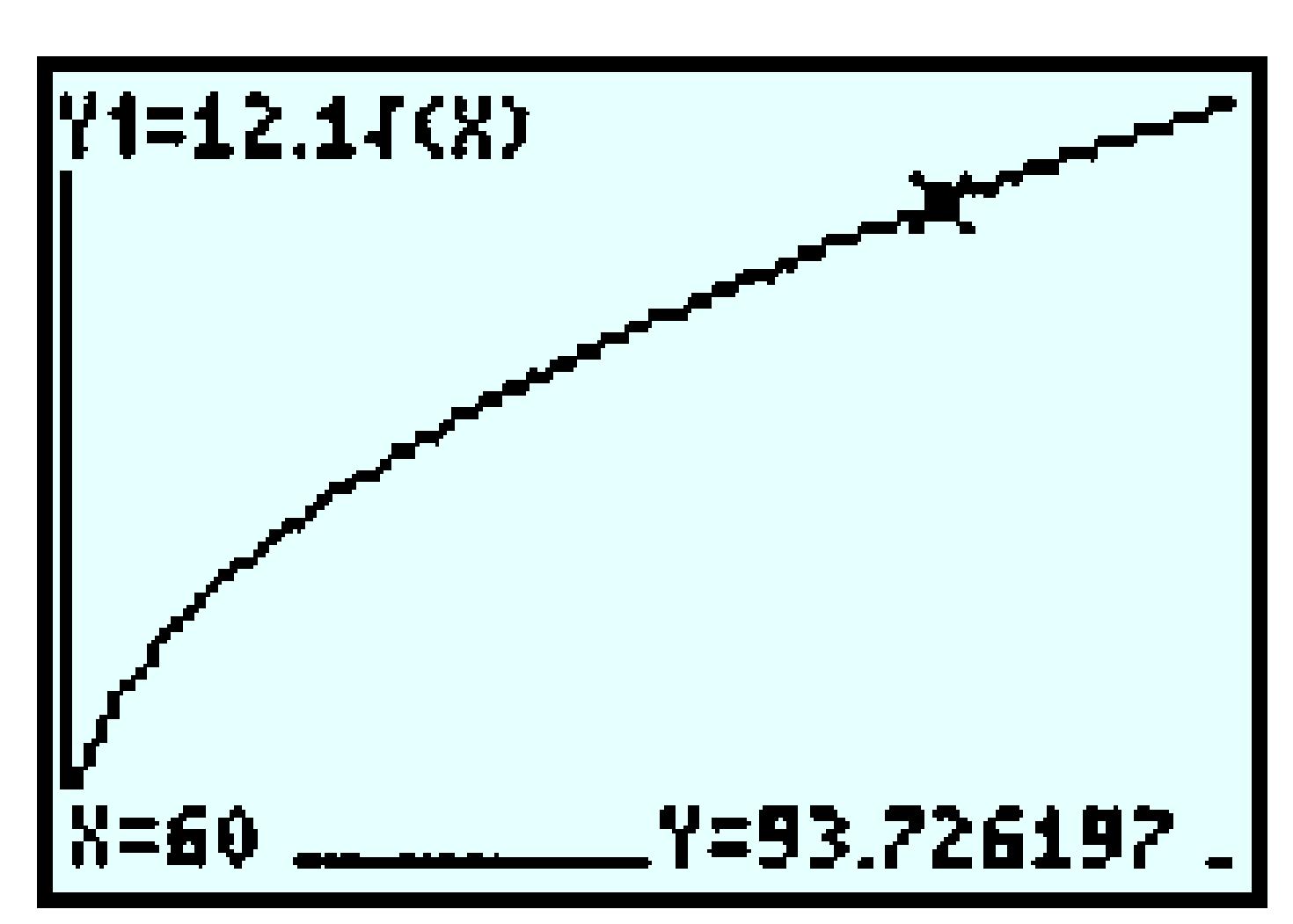
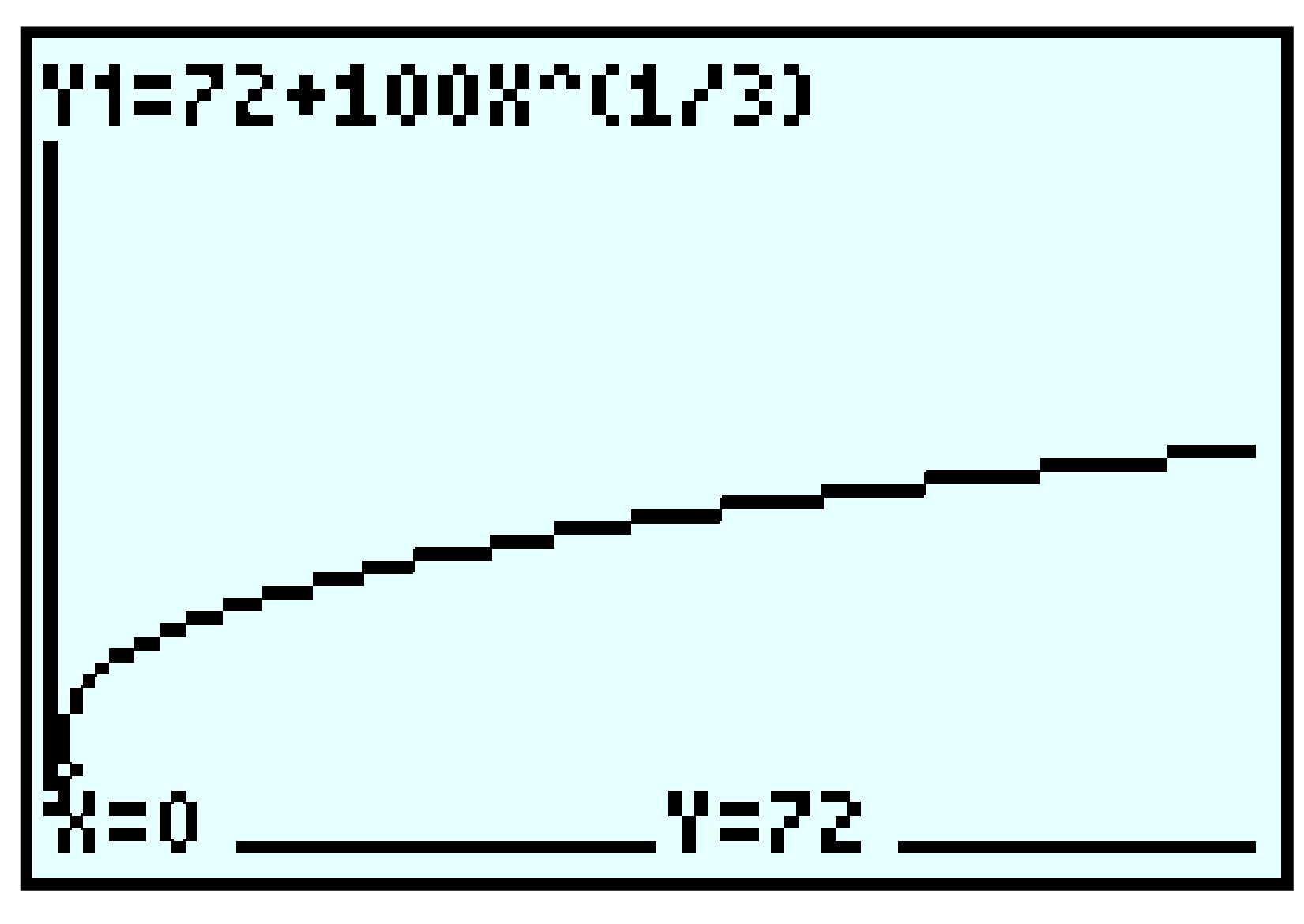
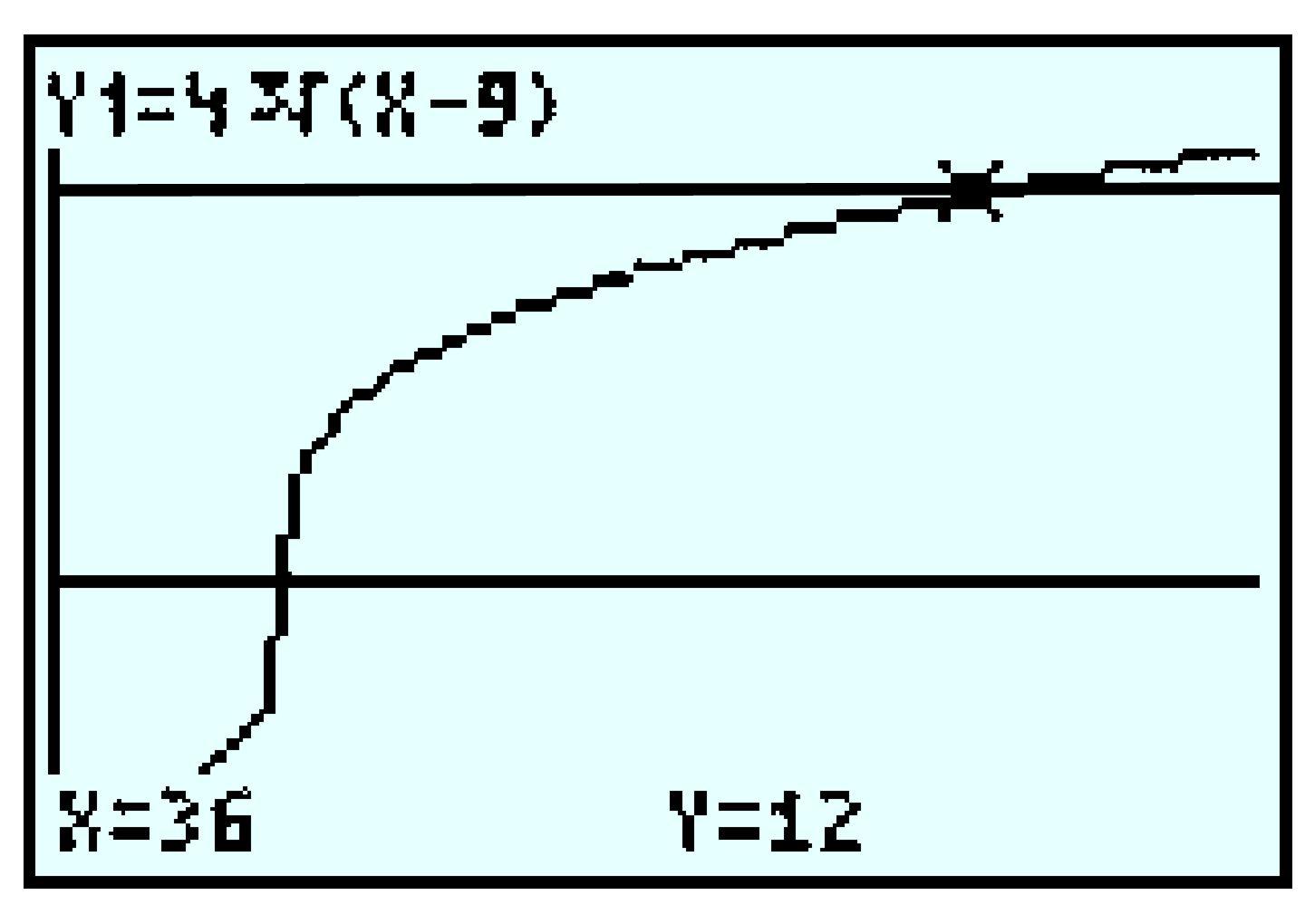
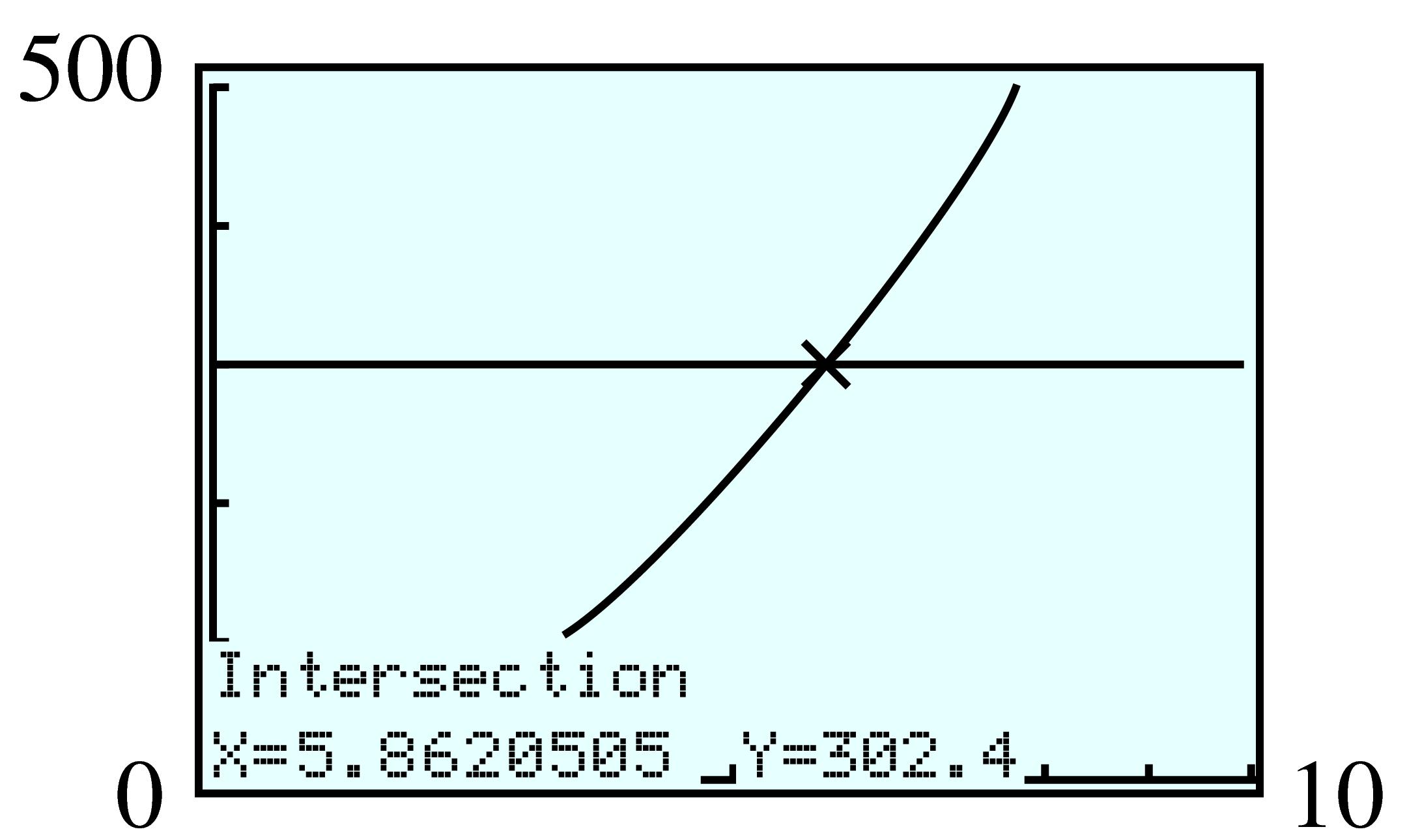
$t$ $5$ $10$ $15$ $20$

$I(t)$ $131 $ $199 $ $254 $ $302 $

Range: $[0, 302]$
$\approx 19.812$ or about $20$ days

21.

Answer.

All the graphs are increasing and concave up. For $x \gt 1\text{,}$ each graph increases more quickly than the previous one.

23.

Answer.

$V = L^3\text{,}$ $A = 6L^2$
$L=V^{1/3}\text{,}$ $L=\left(\dfrac{A}{6} \right)^{1/2}$
$\displaystyle A=6V^{2/3}$
$\dfrac{A}{V}=\frac{6}{L} \text{.}$ As $L$ increases, the surface-to-volume ratio decreases.

25.

Answer.

$$7114.32$

27.

Answer.

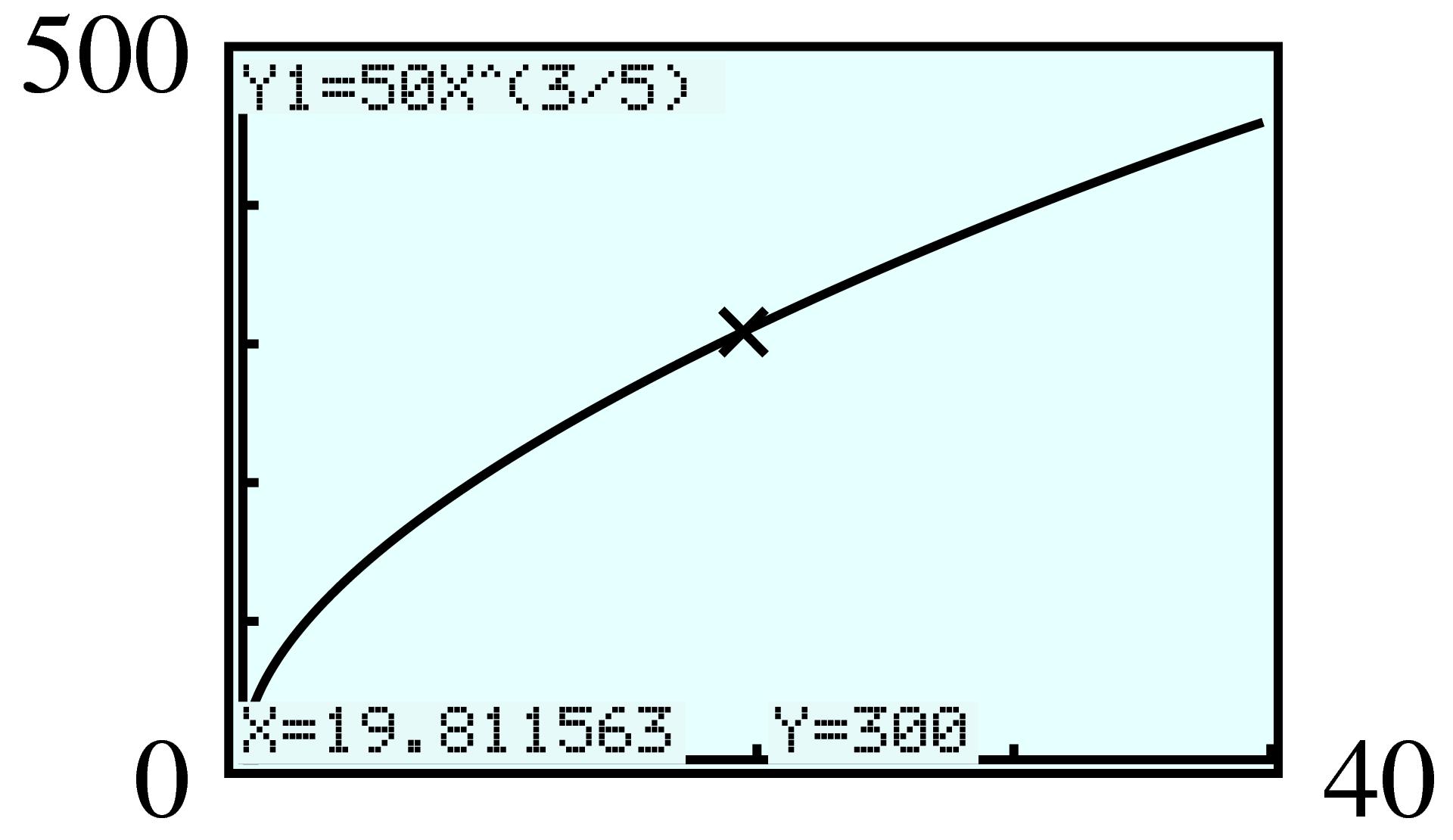
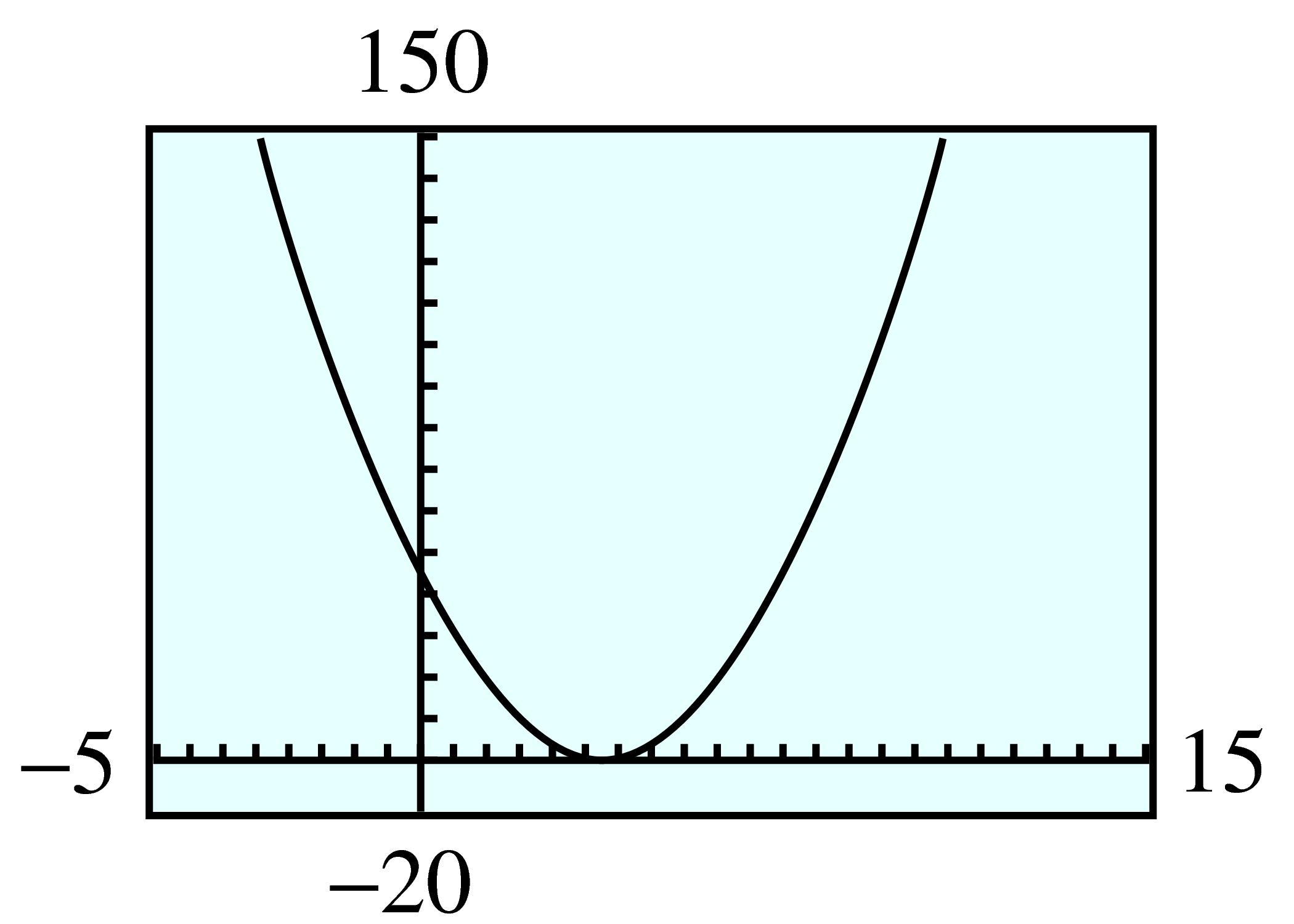
$A$ $10$ $100$ $1000$ $5000$ $10,000$

$S$ $25 $ $42 $ $69 $ $98 $ $115 $
$81\text{,}$ $71$
$126,000$ sq km

29.

Answer.

Home range size: II, lung volume: III, brain mass: I, respiration rate: IV
If $p\gt 1\text{,}$ the graph is increasing and concave up. If $0\lt p\lt 1\text{,}$ the graph is increasing and concave down. If $p\lt 0\text{,}$ the graph is decreasing and concave up.

31.

Answer.

Tricosanthes is the snake gourd and Lagenaria is the bottle gourd. Tricosanthes is thinner and Lagenaria is fatter.
$\displaystyle a\approx 9.5$
$\displaystyle a\approx 2$
Yes

33.

Answer.

$79$ species
$18.4\degree$C
$f (9)\approx 85\text{,}$ $f (10)\approx 79\text{,}$ $f (19)\approx 49\text{,}$ $f (20)\approx 47\text{;}$ from $9\degree$C to $10\degree$C has the greater decrease, corresponding to the steeper slope.

35.

Answer.

$\displaystyle P=\dfrac{k}{\pi}d^{p-2} $
The power function is a good fit on this interval.
$\displaystyle 1.3$

37.

Answer.

$\displaystyle 4a^2$
$\displaystyle 9b^{5/3} $

39.

Answer.

$\displaystyle 4w^{3/2} $
$\displaystyle 3z^2 $

41.

Answer.

$\displaystyle \dfrac{1}{2k^{1/4}} $
$\displaystyle \dfrac{4}{3h^{1/3}} $

43.

Answer.

Wren: $15$ days, greylag goose: $28$ days
$\displaystyle \dfrac{I(m)\cdot W(m)}{m}=0.18m^{-0.041} $
Because $m^{-0.041}$ is close to $m^0\text{,}$ the fraction lost is close to $0.18\text{.}$

45.

Answer.

$x = 64$

47.

Answer.

$x = \dfrac{1}{243} $

49.

Answer.

$x\approx 2.466 $

51.

Answer.

$\displaystyle p= 1.115\times 10^{-12} a^{3/2}$
$1.88$ years

53.

Answer.

$\dfrac{13}{3} $

55.

Answer.

$0.665 $

57.

Answer.

$2x^{3/2} - 2x$

59.

Answer.

$\dfrac{1}{2}y^{1/3}+\dfrac{3}{2}y^{-7/6} $

61.

Answer.

$2x^{1/2} - x^{1/4} - 1 $

63.

Answer.

$a^{3/2}-4a^{3/4}+4 $

65.

Answer.

$x(x^{1/2} + 1)$

67.

Answer.

$\dfrac{y-1}{y^{1/4}} $

69.

Answer.

$\dfrac{a^{2/3}+a^{1/3}-1}{a^{1/3}} $

3.5 Joint Variation
Homework 3.5

1.

Answer.

$\displaystyle R = f (x, y) = 129x + 240y$
$f (24, 12) = 5976$ dollars is the maximum revenue.

3.

Answer.

$f\left(4,\dfrac{3}{2}\right)=\dfrac{25}{12}\approx 2.1 $ inches
No: We do not have $r = kL^2$ for any constant $k\text{.}$
When $L = 2r$ and $h = r\text{,}$ $f (L, h) = r\text{.}$

5.

Answer.

$16,220$ sq cm
Height
$\displaystyle 4.1\%$

7.

Answer.

$\displaystyle C = f (s,w)$
$f (4.5, 160) = 110\text{,}$ so someone walking $4.5$ mph and weighing $160$ pounds burns $110$ calories per mile.
$s\gt 4.5\text{.}$ A person who weighs $160$ pounds must walk faster than $4.5$ mph in order to burn more than $110$ calories per mile.
$7$ mph
Find the row with your walking speed in the left column and move along that row until you are in the column with your weight at the top. The value in that row and column is the number of calories you burn per mile.

9.

Answer.

When is $f (r, 20)\le 800\text{?}$ $~r \le7\%\text{;}$ When is $f (r, 30) \le 800\text{?}$ $~r\le 9\%$
Reducing interest rate by $5\%$
No
No
$30$-year loan

11.

Answer.

Direct variation: In each row, $E = km$ for some constant $k$ that depends on the row.
Inverse variation: In each column, $E = \dfrac{c}{g}$ for some constant $c$ that depends on the column.
$E = \dfrac{m}{g}$ miles/gallon

13.

Answer.

In each row, $R = kp$ for some constant $k$ that depends on the row.
In each column, $R = cd^2$ for some constant $c$ that depends on the column.
$\displaystyle R = 1.57d^2 p$
$588.75$ pounds: When we keep $p$ constant and double $d\text{,}$ $R$ is multiplied by a factor of $4\text{.}$ So the value at $d = 2\frac{1}{2} \text{,}$ $p = 60$ should be $4$ times the value at $d = 1\frac{1}{4} \text{,}$ $p = 60\text{.}$

15.

Answer.

$\displaystyle a=\dfrac{2d}{t^2} $
Mercedes-Benz: $19.05~ \text{ft}/\text{sec}^2\text{,}$ Porsche: $19.73~ \text{ft}/\text{sec}^2\text{,}$ Dodge: $20.47~ \text{ft}/\text{sec}^2\text{,}$ Saleen: $23.59~ \text{ft}/\text{sec}^2\text{,}$ Ford: $25.66~ \text{ft}/\text{sec}^2$

17.

Answer.

$\displaystyle L = \dfrac{3.2v^3}{R}$
Increased by $72.8\%$
Decreased by $16\frac{2}{3}\%$

19.

Answer.

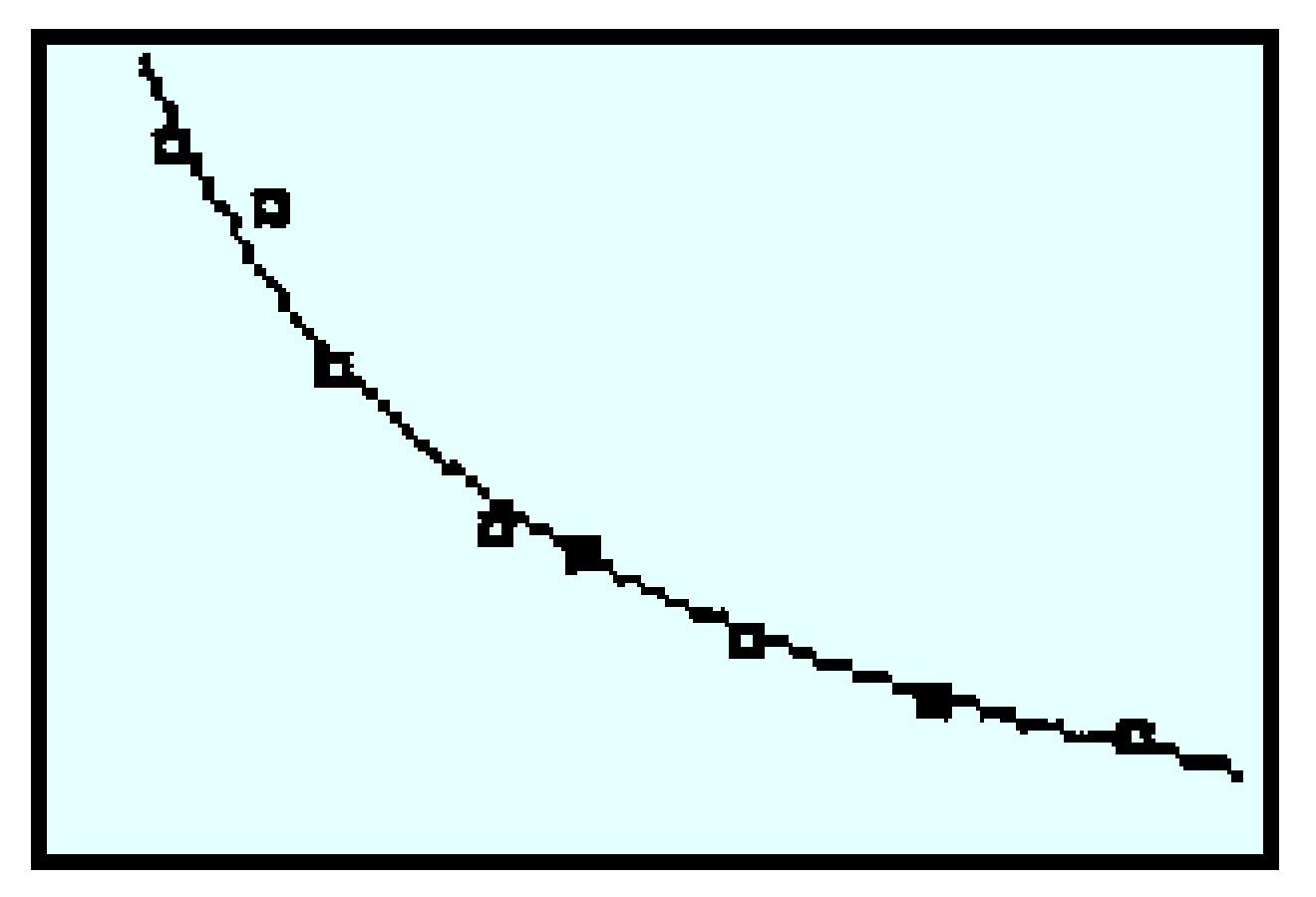
Percent Ammonia
	Pressure (atmospheres)
Temperature ($\degree$C)	$50$	$100$	$150$	$200$	$250$	$300$	$350$	$400$
$350$	$25$	$38$	$46$	$53$	$58$	$62$	$66$	$68$
$400$	$16$	$26$	$33$	$38$	$45$	$48$	$53$	$56$
$450$	$9$	$17$	$23$	$28$	$32$	$37$	$40$	$43$
$500$	$6$	$11$	$16$	$20$	$23$	$27$	$29$	$32$
$550$	$4$	$8$	$11$	$14$	$17$	$19$	$22$	$24$

The ammonia yield decreases.

3.6 Chapter Summary and Review
Chapter 3 Review Problems

1.

Answer.

$\displaystyle d = 1.75t^2$
$63$ cm

3.

Answer.

$480$ bottles

5.

Answer.

$\displaystyle w = \dfrac{k}{r^2}$
$3960\sqrt{3}\approx 6860$ miles

7.

Answer.

$y = 1.2x^2$

9.

Answer.

$y =\dfrac{20}{x} $

11.

Answer.

$\displaystyle \dfrac{1}{81} $
$\displaystyle \dfrac{1}{64} $

13.

Answer.

$\displaystyle \dfrac{1}{243m^5} $
$\displaystyle \dfrac{-7}{y^8} $

15.

Answer.

$\displaystyle \dfrac{2}{c^3} $
$\displaystyle \dfrac{99}{z^2} $

17.

Answer.

$\displaystyle 25\sqrt{m} $
$\displaystyle \dfrac{8}{\sqrt[3]{n}} $

19.

Answer.

$\displaystyle \dfrac{1}{\sqrt[4]{27q^3}} $
$\displaystyle 7\sqrt{u^3v^3} $

21.

Answer.

$\displaystyle 2x^{2/3} $
$\displaystyle \dfrac{1}{4}x^{1/4} $

23.

Answer.

$\displaystyle 6b^{-3/4} $
$\displaystyle \dfrac{-1}{3}b^{-1/3} $

25.

Answer.

27.

Answer.

29.

Answer.

$f(x)=\dfrac{2}{3}x^{-4} $

31.

Answer.

$x$ $16$ $\dfrac{1}{4} $ $3$ $100$

$Q(x)$ $4096 $ $\dfrac{1}{8} $ $4\sqrt{3^5}\approx 62.35 $ $400,000$

33.

Answer.

$x$ $0$ $1 $ $5$ $10$ $20$ $50$ $70$ $100$

$f(x)$ $0 $ $1 $ $1.62$ $2.00 $ $2.46 $ $3.23$ $3.58$ $3.98$

35.

Answer.

$112$ kg

37.

Answer.

283
2051

39.

Answer.

It is the cost of producing the first ship.
$C = \dfrac{12}{ \sqrt[8]{x}} $ million
About $$11$ million; about $8.3\%$ ; about $8.3\%$
About $8.3\%$

41.

Answer.

$t=10$

43.

Answer.

$x=7$

45.

Answer.

$x=5$

47.

Answer.

$x=75$

49.

Answer.

$y=29,524$

51.

Answer.

$g=\dfrac{2v}{t^2} $

53.

Answer.

$p=\pm 2 \sqrt{R^2-R} $

55.

Answer.

$49t^2$

57.

Answer.

$\dfrac{k^7}{64} $

59.

Answer.

$8a^2 $

61.

Answer.

$132.6$ km

63.

Answer.

$\displaystyle 480$
$\displaystyle 498$

65.

Answer.

$$450$
$t = 8\text{:}$ It costs $$864$ to insulate a ceiling with $8$ cm of insulation over an area of $600$ square meters.
$\displaystyle C = 0.72A$
$\displaystyle C = 18T$
$\displaystyle C = 0.18AT$
$$1440$

67.

Answer.

$N =\dfrac{k}{d^2E^3}\text{,}$ where $N$ is number of people, $d$ is distance in miles from the road, $E$ is the elevation gain, and $k$ is the constant of variation.
$\displaystyle k\approx 0.01 $
$\displaystyle 3$

4 Exponential Functions
4.1 Exponential Growth and Decay
Homework 4.1

1.

Answer.

$$28$
$$31.36$

3.

Answer.

It is $99\%$ of what it was $2$ years ago.

5.

Answer.

$P = 1200 + 150t\text{;}$ $1650$
$P = 1200\cdot 1.5^t\text{;}$ $4050$

7.

Answer.

$V = 18,000 - 2000t\text{;}$ $$8000$
$V = 18,000\cdot 0.8^t\text{;}$ $$5898.24$

9.

Answer.

A: $20\%\text{;}$ B: $2\%\text{;}$ C: $7.5\%\text{;}$ D: $100\%\text{;}$ E: $115\%$

11.

Answer.

$\displaystyle P = 20,000\cdot 2.5^{t/6}$
$36,840$ bees; $424,128$ bees

13.

Answer.

$\displaystyle A = 4000\cdot 1.08^t$
$$4665.60\text{;}$ $$8635.70$

15.

Answer.

$\displaystyle P = 200,000\cdot 1.05^t$
$$359,171\text{;}$ $$746,691$

17.

Answer.

$\displaystyle P = 250,000\cdot 0.75^{t/2}$
$162,380\text{;}$ $79,102$

19.

Answer.

$\displaystyle L = 0.85^{d/4}$
$44\%\text{;}$ $16\%$

21.

Answer.

$\displaystyle P = 50\cdot 0.992^t$
$46.1$ lb; $22.4$ lb

23.

Answer.

$\displaystyle 3^{x+4}$
$\displaystyle 3^{4x}$
$\displaystyle 12^x $

25.

Answer.

$\displaystyle b^{-2t} $
$\displaystyle b^{t/2} $
$\displaystyle 1$

27.

Answer.

$P (t + 1) = 12 (3)^{t+1}= 12 (3)^{t}\cdot 3= P(t) \cdot 3 $

29.

Answer.

$P (x+k) = P_0 a^{x+k} = P_0 a^{x}\cdot a^k = P(x) \cdot a^k $

31.

Answer.

In the expression $2\cdot 3^t\text{,}$ only the $3$ is raised to a power $t\text{,}$ and the result is doubled, but if both the $2$ and the $3$ were raised to the power $t\text{,}$ the result would be $6^t\text{.}$
$t$ $0$ $1$ $2$

$P(t)$ $2$ $6$ $18$

$Q(t)$ $1$ $6$ $36$

33.

Answer.

$4$

35.

Answer.

$1.2$

37.

Answer.

$r\approx 0.14$

39.

Answer.

$r\approx 0.04$

41.

Answer.

$\displaystyle P(t) = 1,545,387b^t$
Growth factor $1.049\text{;}$ Percent rate of growth $4.9\%$
$\displaystyle 2,493,401$

43.

Answer.

$\displaystyle 365$
$\displaystyle N(t) = 365(0.356)^t$
$0.03\text{.}$ (Therefore, none)

45.

Answer.

The growth factor is $1.5\text{.}$

$t$	$0$	$1$	$2$	$3$	$4$
$P$	$~8~$	$12$	$18$	$27$	$40.5$

47.

Answer.

The growth factor is $1.2\text{.}$

$x$	$0$	$1$	$2$	$3$	$4$
$Q$	$20$	$24$	$28.8$	$34.56$	$41.47$

49.

Answer.

The decay factor is $0.8\text{.}$

$w$	$0$	$1$	$2$	$3$	$4$
$N$	$120$	$96$	$76.8$	$61.44$	$49.15$

51.

Answer.

The decay factor is $0.8\text{.}$

$t$	$0$	$1$	$2$	$3$	$4$
$C$	$10$	$8$	$6.4$	$5.12$	$4.10$

53.

Answer.

The growth factor is $1.1\text{.}$

$n$	$0$	$1$	$2$	$3$	$4$
$B$	$200$	$220$	$242$	$266.2$	$292.82$

55.

Answer.

Initial value $4\text{,}$ growth factor $2^{1/3}$
$\displaystyle f (x) = 4\cdot 2^{x/3}$

57.

Answer.

Initial value $80\text{,}$ decay factor $\frac{1}{2}$
$\displaystyle f (x) = 80\cdot \left(\dfrac{1}{2} \right)^x $

59.

Answer.

$84.6\%\text{,}$ $55.8\%$

61.

Answer.

No, an increase of $48\%$ in $6$ years corresponds to a growth factor of $1.48^{1/6}\approx 1.0675\text{,}$ or an annual growth rate of about $6.75\%\text{.}$

63.

Answer.

$\displaystyle P(t) = 16,986,335(1 + r)^t$
$\displaystyle 2.07\%$

65.

Answer.

$\displaystyle 3.53\%$
$\displaystyle 3.53\%$
No
$\displaystyle 3.53\%$

67.

Answer.

$39\text{;}$ $1.045$
$35\text{;}$ $1.047$
Species B

69.

Answer.

$t$ $0$ $2$ $4$ $6$ $8$

$L(t)$ $3$ $6$ $9$ $12$ $15$

$\displaystyle L(t) = 3 + 1.5t$
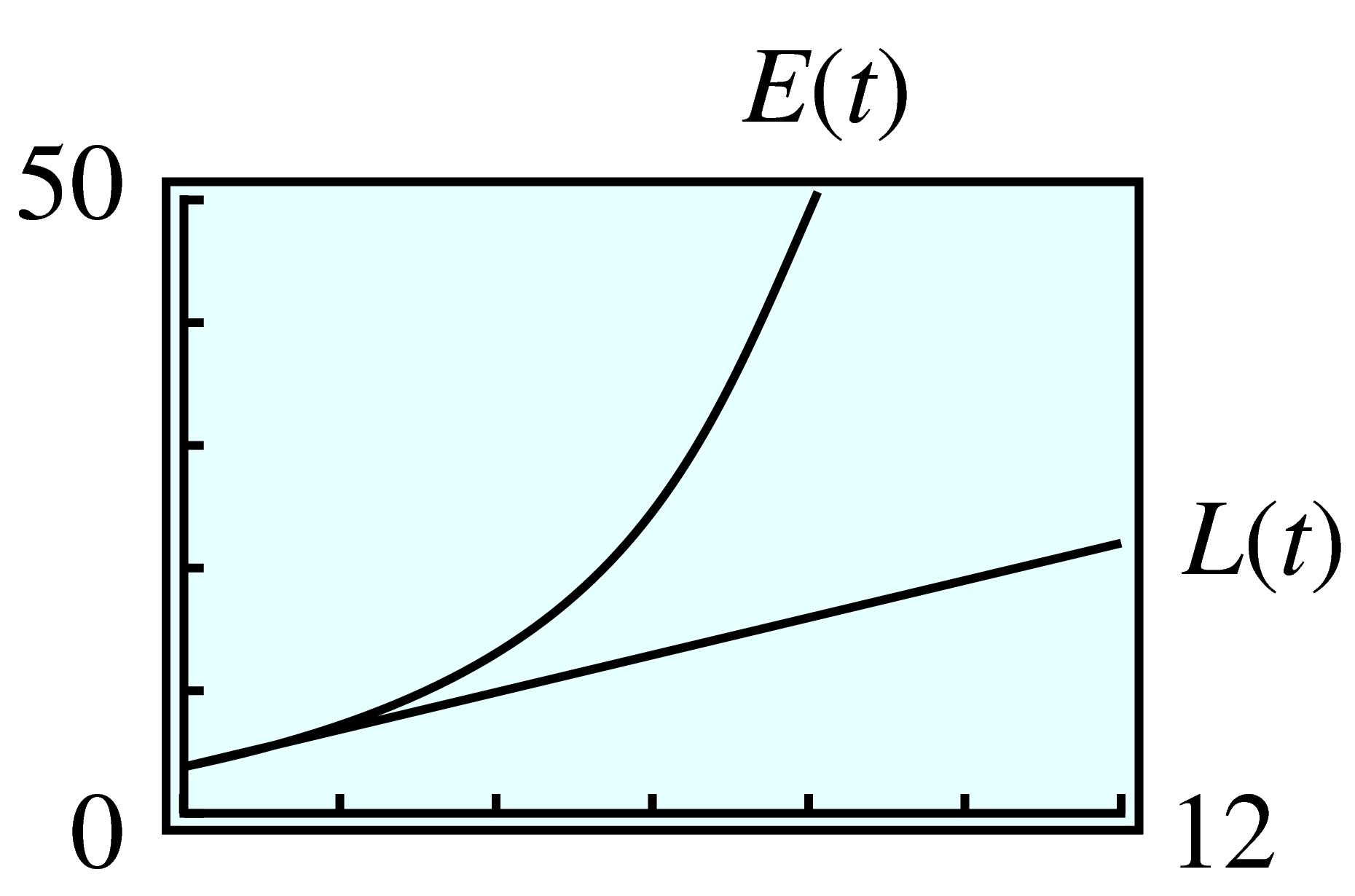
$t$ $0$ $2$ $4$ $6$ $8$

$E(t)$ $3$ $6$ $12$ $24$ $48$

$\displaystyle E(t) = 3\cdot 2^{t/2}$

71.

Answer.

$244$ tigers per year
$0.97\text{;}$ $3\%$
Linear: $3067\text{;}$ Exponential: $4170$

4.2 Exponential Functions
Homework 4.2

1.

Answer.

$26\text{;}$ increasing
$1.2\text{;}$ decreasing
$75\text{;}$ decreasing
$\frac{2}{3} \text{;}$ increasing

3.

Answer.

$x$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
$f(x)=3^x $	$\frac{1}{27} $	$\frac{1}{9} $	$\frac{1}{3} $	$1$	$3$	$9$	$27$
$g(x)=\left(\frac{1}{3} \right)^x $	$27$	$9$	$3$	$1$	$\frac{1}{3} $	$\frac{1}{9} $	$\frac{1}{27} $

The two graphs are reflections of each other across the $y$-axis. $f$ is increasing, $g$ is decreasing. $f$ has the negative $x$-axis as an asymptote, and $g$ has the positive $x$-axis as its asymptote.

5.

Answer.

$t$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$
$h(t)=4^{-t} $	$64$	$16$	$4$	$1$	$\frac{1}{4} $	$\frac{1}{16} $	$\frac{1}{64} $
$q(t)=-4^t $	$\frac{-1}{64} $	$\frac{-1}{16} $	$\frac{-1}{4} $	$-1$	$-4$	$-16$	$-64$

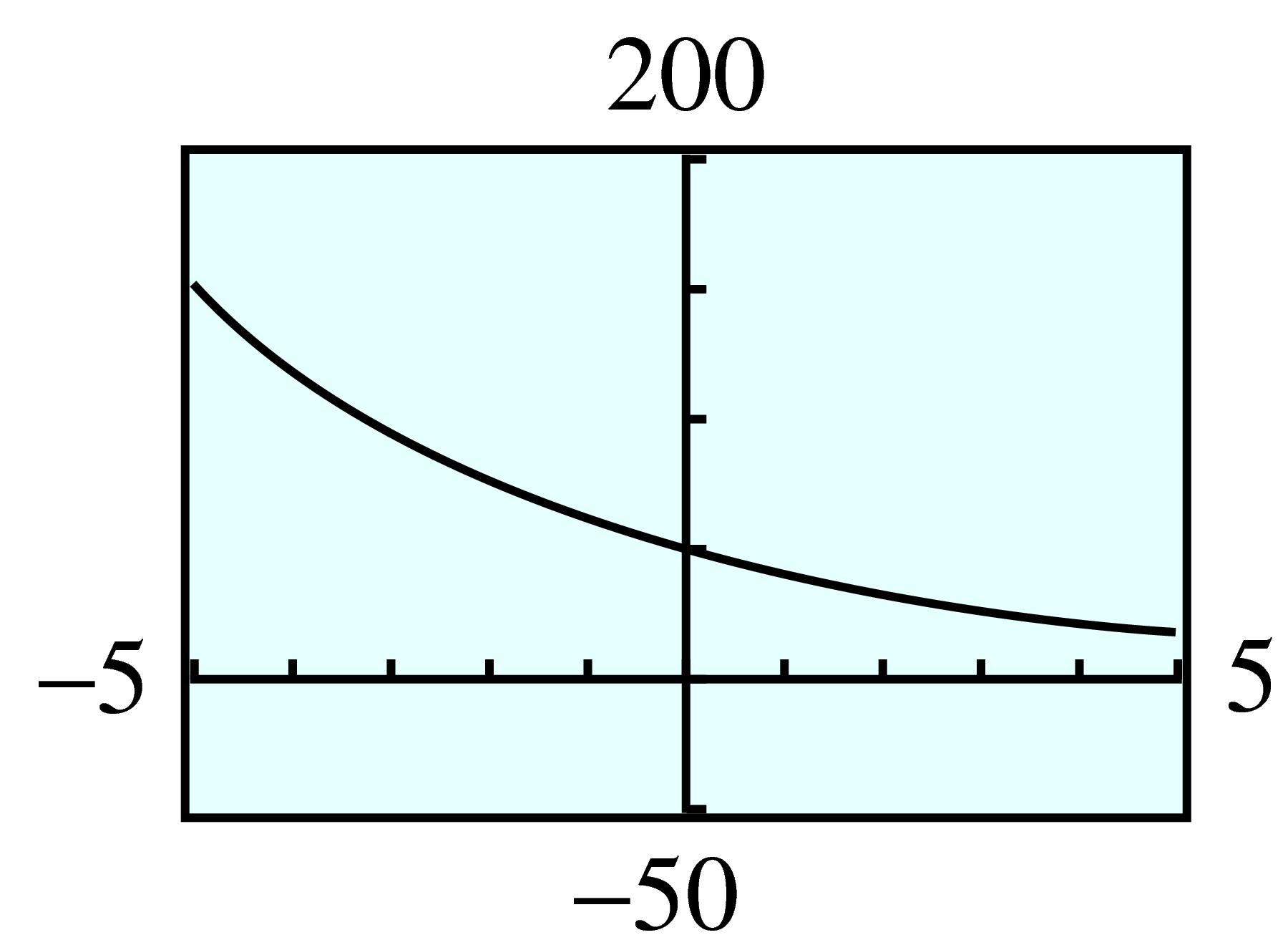
exponential decay and negative of growth

The graphs are reflections of each other across the origin. Both are decreasing, but $h$ has the negative $t$-axis as an asymptote, and $q$ has the positive t-axis as its asymptote.

7.

Answer.

9.

Answer.

$\displaystyle [1.08, 14.85] $

11.

Answer.

$\displaystyle [16.38, 152.59]$

13.

Answer.

Because they are defined by equivalent expressions, (b), (c), and (d) have identical graphs

15.

Answer.

To evaluate $f$ we subtract $1$ from the input before evaluating the exponential function; to evaluate $g$ we subtract $1$ from the output of the exponential function.

$x$	$y=2^x$	$f(x)$	$g(x)$
$-2$	$\dfrac{1}{4} $	$\dfrac{1}{8} $	$\dfrac{-3}{4} $
$-1$	$\dfrac{1}{2} $	$\dfrac{1}{4} $	$\dfrac{-1}{2} $
$0$	$1 $	$\dfrac{1}{2} $	$0 $
$1$	$2 $	$1 $	$1 $
$2$	$4 $	$2 $	$3 $

The graph of $f$ is translated $1$ unit to the right; the graph of $g$ is shifted $1$ unit down.

17.

Answer.

To evaluate $f$ we take the negative of the output of the exponential function; to evaluate $g$ we take the negative of the input.

$x$	$y=3^x$	$f(x)$	$g(x)$
$-2$	$\dfrac{1}{9} $	$\dfrac{-1}{9} $	$9 $
$-1$	$\dfrac{1}{3} $	$\dfrac{-1}{3} $	$3 $
$0$	$1 $	$-1 $	$1 $
$1$	$3 $	$-3 $	$\dfrac{1}{3} $
$2$	$9 $	$-9 $	$\dfrac{1}{9} $

The graph of $f$ is reflected about the $x$-axis; the graph of $g$ is reflected about the $y$-axis.

19.

Answer.

$3(5^{a+2})$ is not equivalent to $9\cdot 3(5^a)\text{.}$
$3(5^{2a})$ is not equivalent to $2\cdot 3 (5^a)\text{.}$

21.

Answer.

$8^w - 8^z$ is not equivalent to $8^{w-z}\text{.}$
$8^{-x}$ is equivalent to $\dfrac{1}{8^x}\text{.}$

23.

Answer.

$\displaystyle P_0=300$
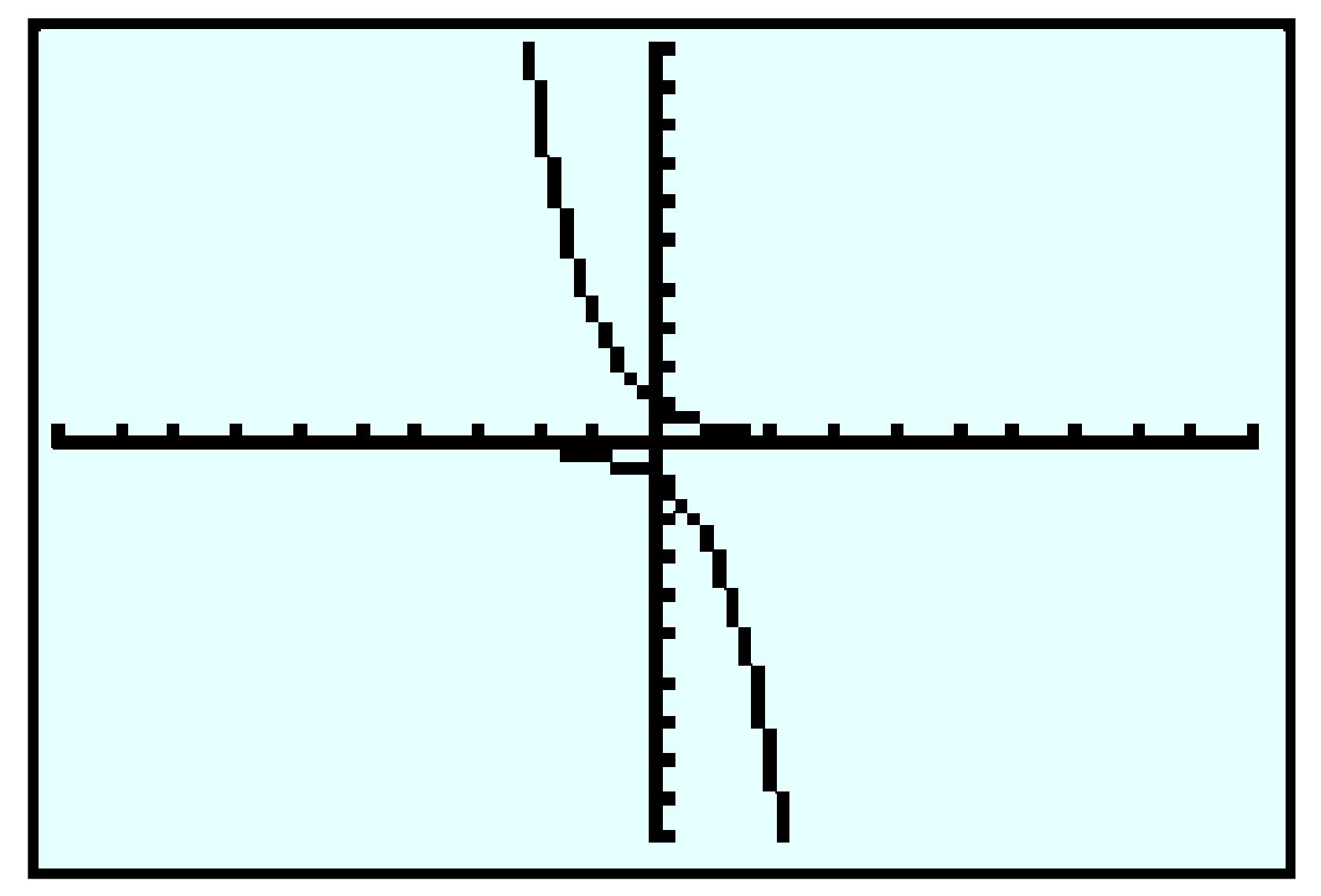
$x$ $0$ $1$ $2$

$f(x)$ $300$ $600$ $1200$
$\displaystyle b=2$
$\displaystyle f(x)=300(2)^x $

25.

Answer.

$\displaystyle S_0=150$
$\displaystyle b\approx 0.55$
$\displaystyle S(d) = 150(0.55)^d$

27.

Answer.

$\dfrac{2}{3} $

29.

Answer.

$\dfrac{-1}{4} $

31.

Answer.

$\dfrac{1}{7} $

33.

Answer.

$\dfrac{-5}{4} $

35.

Answer.

$\pm 2 $

37.

Answer.

$\displaystyle N(t) = 26(2)^{t/6}$
$72$ days later

39.

Answer.

$\displaystyle V(t) = 700(0.7)^{t/2}$
$4$ yr

41.

Answer.

$x = 2.26$

43.

Answer.

$x = -1.40$

45.

Answer.

Power
Exponential
Power
Neither

47.

Answer.

Exponential $y=3\cdot 2^x$
Power $P=0.5 t^2$

49.

Answer.

Power $y=100 x^{-1}$
Exponential $P=\frac{1}{4} \cdot 2^x$

51.

Answer.

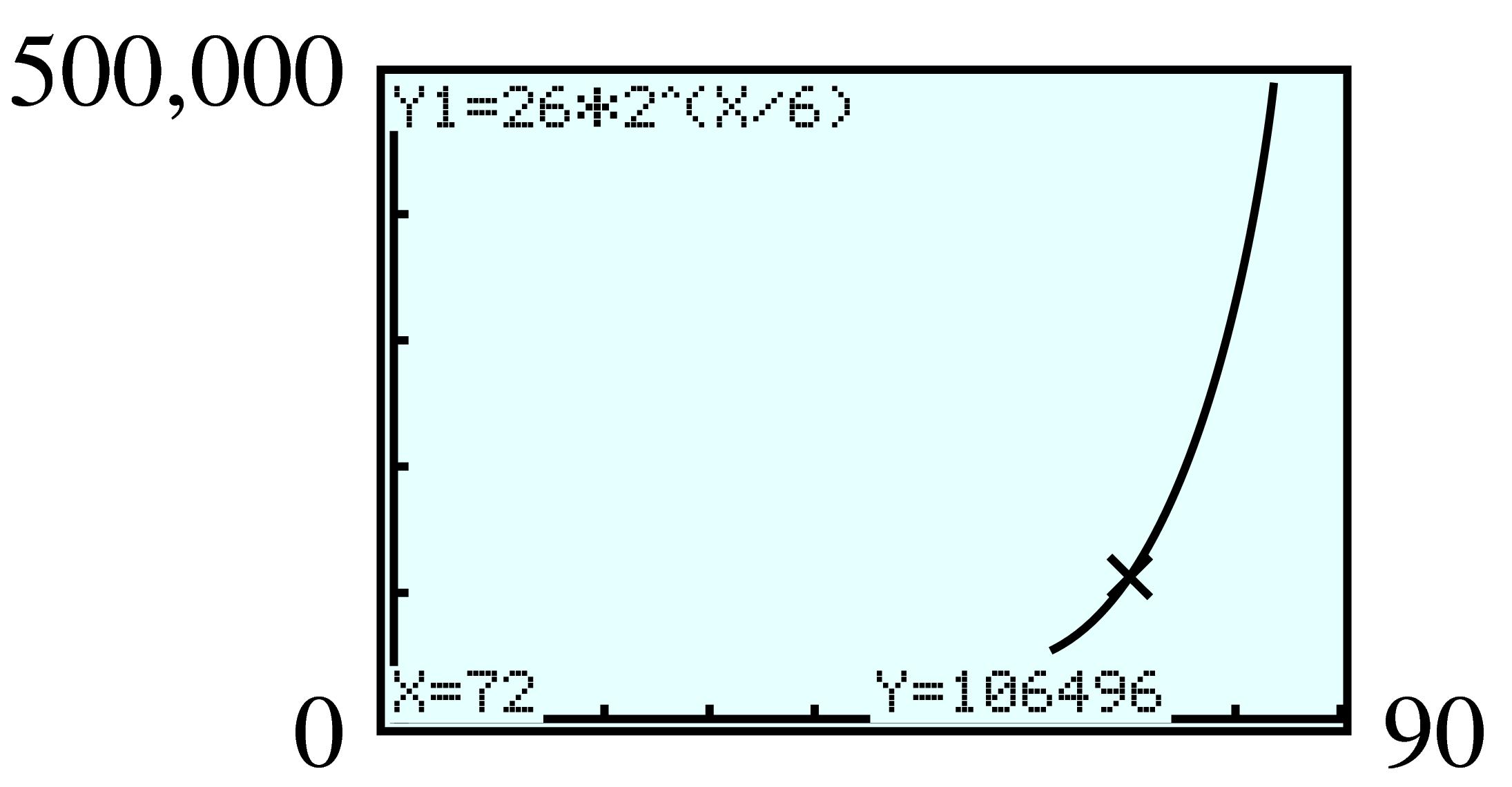
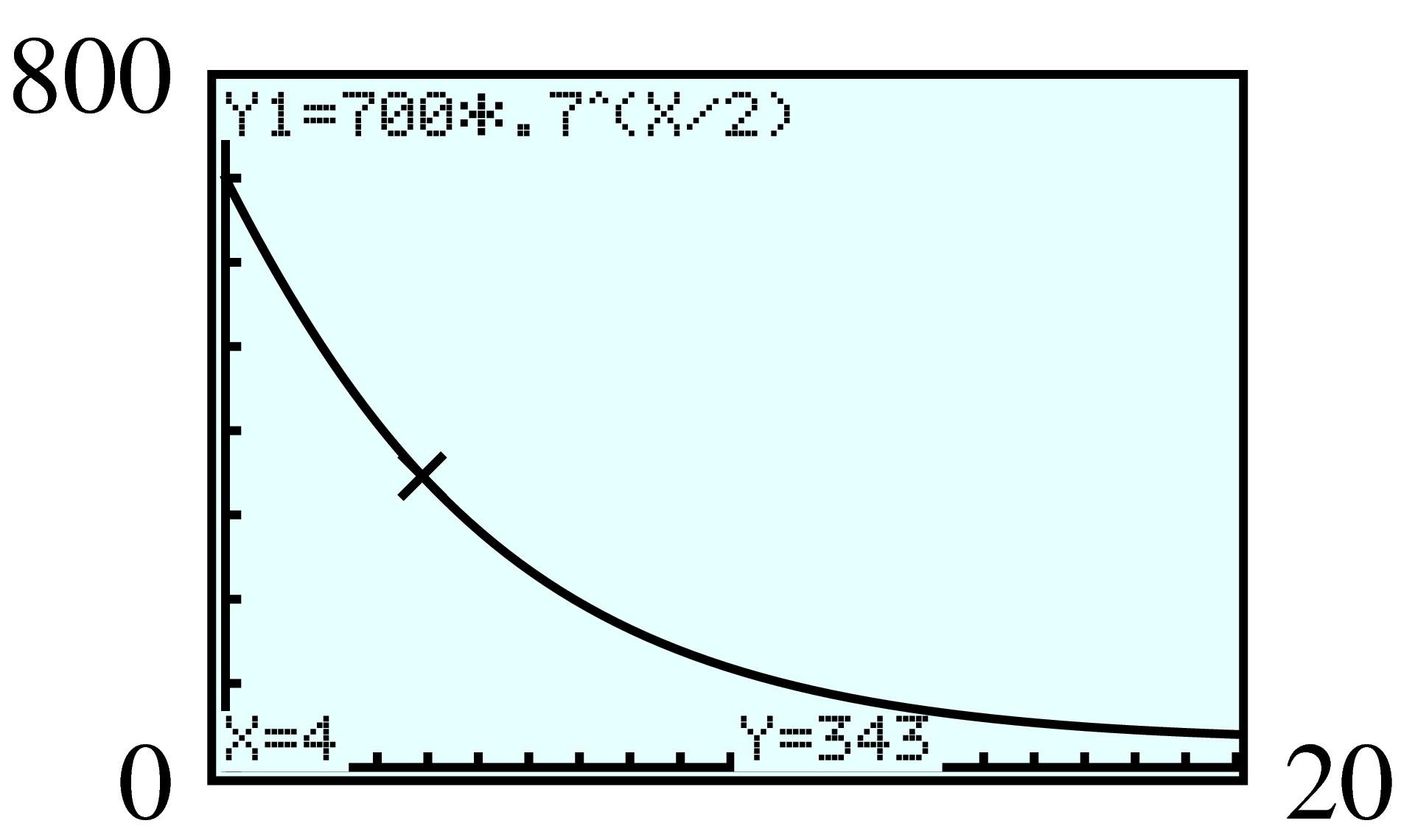
$x$	$f(x)=x^2$	$g(x)=2^x $
$-2$	$4$	$\frac{1}{4} $
$-1$	$1$	$\frac{1}{2} $
$0$	$0$	1
$1$	$1$	$2$
$2$	$4$	$4$
$3$	$9$	$8$
$4$	$16$	$16$
$5$	$25$	$32$

Range of $f\text{:}$ $[0, \infty)\text{;}$ Range of $g\text{:}$ $(0, \infty)$
$\displaystyle 3$
$-0.7667\text{,}$ $2\text{,}$ $4$
$(-0.7667, 2) $ and $(4,\infty)$
g

53.

Answer.

$y = 3^x - 4$

Domain: $(-\infty, \infty)\text{;}$ range: $(-4, \infty)\text{,}$ $x$-intercept $(1.26, 0)\text{;}$ $y$-intercept $(0, -3)\text{;}$ horizontal asymptote $y=-4$
$y=3^{x-4}\text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(0, \infty)\text{,}$ no $x$-intercept; $y$-intercept $\left(0, \dfrac{1}{81}\right)\text{;}$ the $x$-axis is the horizontal asymptote.
$y=-4\cdot 3^{x}\text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(-\infty, 0)\text{,}$ no $x$-intercept; $y$-intercept $(0, -4)\text{;}$ the $x$-axis is the horizontal asymptote.

55.

Answer.

$y =-6^t$

Domain: $(-\infty, \infty)\text{;}$ range: $(-\infty, 0)\text{,}$ no $t$-intercept; $y$-intercept $(0, -1)\text{;}$ the $t$-axis is the horizontal asymptote.
$y=6^{-t}\text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(0, \infty)\text{,}$ no $t$-intercept; $y$-intercept $(0, 1)\text{;}$ the $t$-axis is the horizontal asymptote.
$y=-6^{-t}\text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(-\infty, 0)\text{,}$ no $t$-intercept; $y$-intercept $(0, -1)\text{;}$ the $t$-axis is the horizontal asymptote.

57.

Answer.

$y =2^{x-3}$

Domain: $(-\infty, \infty)\text{;}$ range: $(0, \infty)\text{,}$ no $x$-intercept; $y$-intercept $\left(0, \frac{1}{8}\right)\text{;}$ the $x$-axis is the horizontal asymptote.
$y=2^{x-3}+4 \text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(4, \infty)\text{,}$ no $x$-intercept; $y$-intercept $>\left(0, \frac{33}{8}\right)\text{;}$ horizontal asymptote $y=4$

59.

Answer.

$y =-\left(\dfrac{1}{2}\right)^t$

Domain: $(-\infty, \infty)\text{;}$ range: $(-\infty, 0)\text{,}$ no $t$-intercept; $y$-intercept $(0, -1)\text{;}$ the $t$-axis is the horizontal asymptote.
$y=6-\left(\dfrac{1}{2} \right)^t \text{,}$

Domain: $(-\infty, \infty)\text{;}$ range: $(-\infty,6)\text{,}$ $t$-intercept approximately $(-2.58,0)\text{;}$ $y$-intercept $(0, 5)\text{;}$ horizontal asymptote is $y=6$

61.

Answer.

The graph of $y = 2^x$ has been reflected about the $y$-axis and shifted up $2$ units.
$\displaystyle y=2^{-x}+2 $

63.

Answer.

The graph of $y = 2^x$ has been reflected about the $x$-axis and shifted up $10$ units.
$\displaystyle y=-2^{x}+10 $

65.

Answer.

67.

Answer.

$t$ $3.5$ $4$ $8$ $10$ $15$

$f(t)$ $128$ $154.75$ $184.05$ $150.93$ $103.96$
From $0$ to $3$ minutes, the volunteer is walking with heart rate $100$ beats per minute. The volunteer jogged at a steady pace from $3$ to $4$ minutes, and the heart rate increased to about $155$ beats per minutes. From $4$ to $9$ minutes, the jogging pace increased, and the heart rate rose to about $185$ beats per minute. The cooldown started at $9$ minutes, and the heart rate decreased rapidly and leveled off to about $100$ beats per minute.

4.3 Logarithms
Homework 4.3

1.

Answer.

$\displaystyle 2$
$\displaystyle 5$

3.

Answer.

$\displaystyle \dfrac{1}{2} $
$\displaystyle -1$

5.

Answer.

$\displaystyle 1 $
$\displaystyle 0 $

7.

Answer.

$\displaystyle 5 $
$\displaystyle 6 $

9.

Answer.

$\displaystyle -1 $
$\displaystyle -3 $

11.

Answer.

$\log_2 1024=10$

13.

Answer.

$\log_{10} 5\approx 0.699$

15.

Answer.

$\log_{t} 16=\dfrac{3}{2} $

17.

Answer.

$\log_{0.8} M=1.2 $

19.

Answer.

$\log_{x} (W-3)=5t $

21.

Answer.

$\log_{3} (2N_0)=-0.2t $

23.

Answer.

$\displaystyle \log_4 2.5 $
$\displaystyle 0.7$

25.

Answer.

$\displaystyle \log_{10} 0.003 $
$\displaystyle -2.5$

27.

Answer.

$\displaystyle 0\lt \log_{10} 7 \lt 1$
$\displaystyle 0.85$

29.

Answer.

$\displaystyle 3\lt \log_{3} 67.9 \lt 4$
$\displaystyle 3.84$

31.

Answer.

$\displaystyle 0.7348$
$\displaystyle 1.7348$
$\displaystyle 2.7348$
$\displaystyle 3.7348$

When the input to the common logarithm is multiplied by $10\text{,}$ the output is increased by $1\text{.}$

33.

Answer.

$\displaystyle 0.3010$
$\displaystyle 0.6021$
$\displaystyle 0.9031$
$\displaystyle 1.2041$

When the input to the common logarithm is doubled, the output is increased by about $0.3010\text{.}$

35.

Answer.

$-0.23$

37.

Answer.

$2.53$

39.

Answer.

$0.77$

41.

Answer.

$-0.68$

43.

Answer.

$3.63$

45.

Answer.

$2\cdot 5^x\ne 10^x\text{;}$ the first step should be to divide both sides of the equation by $2\text{;}$ $x = \log_5 424\text{.}$

47.

Answer.

$\frac{10^{4x}}{4} \ne 10^x\text{;}$ the first step should be to write $4x = \log 20\text{;}$ $x = \frac{\log 20}{4}\text{.}$

49.

Answer.

$\displaystyle 33,855,812$
$38,515,295\text{;}$ $~41,080,265\text{;}$ $~43,816,051$
$\displaystyle 2002$
$\displaystyle 2012$

51.

Answer.

$\displaystyle 85.5$
Decreasing; range: $[5.4, 1355.2]$
$\displaystyle 1.45$
$\displaystyle \dfrac{1}{100} $
$\displaystyle 10^{0.4}\approx 2.5119 $
$2.15\times 10^{-6}$ to $855,067$

53.

Answer.

$9.60$ in

55.

Answer.

$1.91$ mi

57.

Answer.

$3.34$ mi

59.

Answer.

$1$

61.

Answer.

$0$

63.

Answer.

$1$

65.

Answer.

$0$

4.4 Properties of Logarithms
Homework 4.4

1.

Answer.

$\displaystyle 10^8 $
$2\text{;}$ $~6\text{;}$ $~8\text{;}$ $~2+6=8$

3.

Answer.

$\displaystyle b^3 $
$8\text{;}$ $~5\text{;}$ $~3\text{;}$ $~8-5=3$

5.

Answer.

$\displaystyle 10^{15} $
$15\text{;}$ $~3\text{;}$ $~15=3\cdot 5$

7.

Answer.

$\displaystyle \log_b 2 + \log_b x$
$\displaystyle \log_b 2 - \log_b x$

9.

Answer.

$\displaystyle 1 + 4\log_3 x$
$\displaystyle \dfrac{1}{t}\log_5 1.1 $

11.

Answer.

$\displaystyle \dfrac{1}{2} + \dfrac{1}{2}\log_b x$
$\displaystyle \dfrac{1}{3}\log_3 (x^2+1) $

13.

Answer.

$\displaystyle \log P_0 + t\log (1-m) $
$\displaystyle 4t [\log_4(4+r)-1] $

15.

Answer.

$\displaystyle \log_b 4$
$\displaystyle \log_4(x^2y^3) $

17.

Answer.

$\displaystyle \log 2x^{5/2} $
$\displaystyle \log (t-4) $

19.

Answer.

$\displaystyle \log \dfrac{1}{27} $
$\displaystyle \log_6 (2w^2) $

21.

Answer.

$\displaystyle 1.7917$
$\displaystyle -0.9163$

23.

Answer.

$\displaystyle 2.1972$
$\displaystyle 1.9560$

25.

Answer.

$2.8074$

27.

Answer.

$0.8928$

29.

Answer.

$\pm 1.3977$

31.

Answer.

$-1.6092$

33.

Answer.

$0.2736$

35.

Answer.

$-12.4864$

37.

Answer.

$\displaystyle S (t) = S_0(1.09)^t$
$4.7$ hours

39.

Answer.

$\displaystyle C (t) = 0.7(0.80)^t$
After $2.5$ hours

41.

Answer.

$\displaystyle J(t) = 1,041,000\cdot 1.0182^t$
In $2040$

43.

Answer.

$\displaystyle S(t) = S_0 \cdot 0.9527^t$
$28.61$ hours

45.

Answer.

$\displaystyle 5$
$\displaystyle 6$
$\displaystyle 5$

(a) and (c) are equal.

47.

Answer.

$\displaystyle 6$
$\displaystyle 9$
$\displaystyle 6$

(a) and (c) are equal.

49.

Answer.

$\displaystyle \log 24\approx 1.38$
$\displaystyle \log 240\approx 2.38$
$\displaystyle \log 230\approx 2.36$

None are equal.

51.

Answer.

$\displaystyle \log 60\approx 1.78$
$\displaystyle \log 5\approx 0.70$
$\displaystyle \dfrac{\log_{10}75}{\log_{10}15}\approx 1.59$

None are equal.

53.

Answer.

$12.9\%$

55.

Answer.

About $11$ years

57.

Answer.

$\displaystyle A=1000\left(1+\dfrac{0.12}{n} \right)^{5n} $
$A$ increases.
$16\text{;}$ $31\text{;}$ $553$
Increasing, concave down, asymptotically approaching $A\approx 1822.12$

59.

Answer.

$k=\dfrac{1}{t}\dfrac{\log(N/N_0)}{\log a} $

61.

Answer.

$t=\dfrac{1}{k}\log\left(\dfrac{A}{A_0}+1\right) $

63.

Answer.

$q=\dfrac{\log(w/p)}{\log v} $

65.

Answer.

$x=b^m \text{,}$ $y=b^n$
$\displaystyle \log_b(b^m\cdot b^n)$
$\displaystyle \log_b(b^m\cdot b^n)=\log_b b^{m+n} $
$\displaystyle \log_b b^{m+n}=m+n $
$\displaystyle \log_b b^{m+n}=(\log_b x)+(\log_b y) $

67.

Answer.

$\displaystyle x=b^m $
$\displaystyle \log_b(b^m)^k$
$\displaystyle \log_b(b^m)^k=\log_b b^{mk} $
$\displaystyle \log_b b^{mk}=mk $
$\displaystyle \log_b b^{mk}=(\log_b x)\cdot k $

4.5 Exponential Models
Homework 4.5

1.

Answer.

$A(x) = 0.14(50)^{x/3}$

3.

Answer.

$f(x) = \dfrac{65,536}{729}\left(\dfrac{3}{4} \right)^x $

5.

Answer.

$M(x) = 62,500(0.2)^x $

7.

Answer.

$s(x) = \dfrac{1}{135}(9)^x $

9.

Answer.

$y=\dfrac{4}{3}(3)^{x/4}$

11.

Answer.

$y=50(2)^{-x/4} $

13.

Answer.

$\displaystyle y= 2.6 -1.3x$
$\displaystyle y = 2.6(0.5)^x$

15.

Answer.

$\displaystyle y= -36-16x $
$\displaystyle y = \dfrac{12}{5}(5)^{-x/3} $

17.

Answer.

$\displaystyle y= 2.5+0.875x $
$\displaystyle y = 1.5(2)^{x/2} $

19.

Answer.

$P = P_0(1.052)^t\text{;}$ $t$ is the number of years since $1990\text{.}$
$\dfrac{\log 2}{\log 1.052}\approx 13.7 $ years

21.

Answer.

$GDP = 1.028^t$ million pounds
$\dfrac{\log 2}{\log 1.028}\approx 25.1 $ years
$50.2$ years

23.

Answer.

$\dfrac{\log 0.5}{\log 0.946}\approx 12.5 $ hours
$25$ hours

25.

Answer.

$\dfrac{\log 0.5}{\log 0.844}\approx 4.1 $ hours
$8.2$ hours

27.

Answer.

$\displaystyle P = 2000(2)^{t/5} $
$\displaystyle 14.87\% $

29.

Answer.

$\displaystyle D = D_0 \left(\dfrac{1}{2} \right)^{t/18} $
$\displaystyle 3.78\% $

31.

Answer.

$\displaystyle A = A_0 \left(\dfrac{1}{2} \right)^{t/1620 }$
$\displaystyle 0.043\%$

33.

Answer.

$\displaystyle P = P_0 (2)^{t/25 }$
$\displaystyle 2.81\%$

35.

Answer.

$\displaystyle ab^D = 2\cdot ab^0 = 2a$
$\displaystyle b^D=2$
$\displaystyle f (t + D) = ab^{t+D} = a\cdot b^t\cdot b^D = ab^t\cdot 2 = 2 f (t)$
For any value of $t\text{,}$ after $D$ units of time, the new value of $f$ is $2$ times the old value.

37.

Answer.

$\displaystyle ab^R = \frac{1}{3} \cdot ab^0 = \frac{1}{3} a$
$\displaystyle b^R=\frac{1}{3} $
$\displaystyle g(t + R) = ab^{t+R} = a\cdot b^t\cdot b^R = ab^t\cdot \frac{1}{3} = \frac{1}{3} g(t)$
For any value of $t\text{,}$ after $R$ units of time, the new value of $g$ is $\frac{1}{3} $ times the old value.

39.

Answer.

$\displaystyle A = A_0 \left(\dfrac{1}{2} \right)^{t/5730}$
About $760$ years old

41.

Answer.

$\displaystyle A = A_0 \left(\dfrac{1}{2} \right)^{t/432}$
About $220$ years

43.

Answer.

$\approx 30$ years; $\approx 33$ years

45.

Answer.

$$445.89\text{;}$ $$376.50$

47.

Answer.

$\displaystyle N(t) = 2200(2)^{t/1.5}$
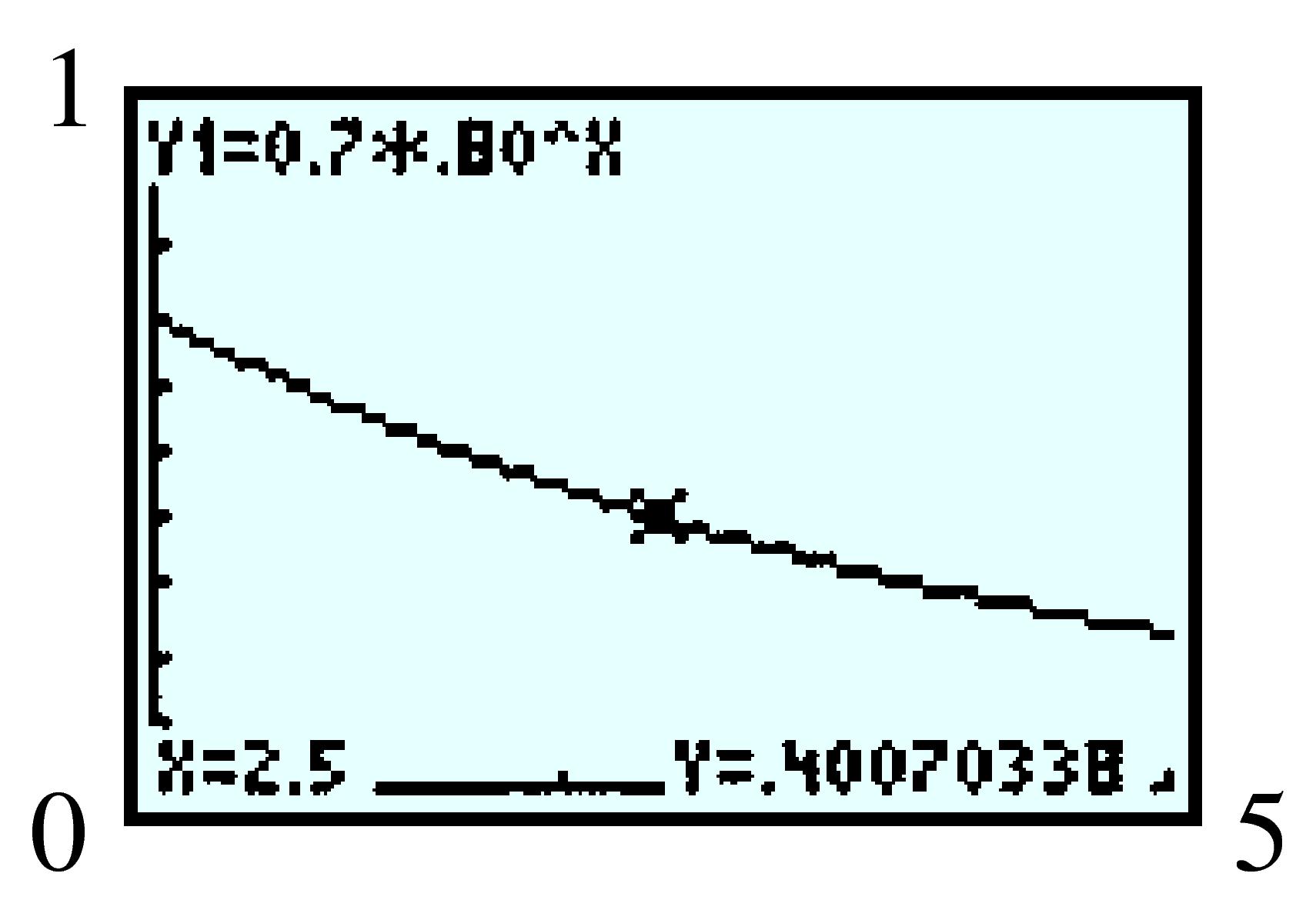
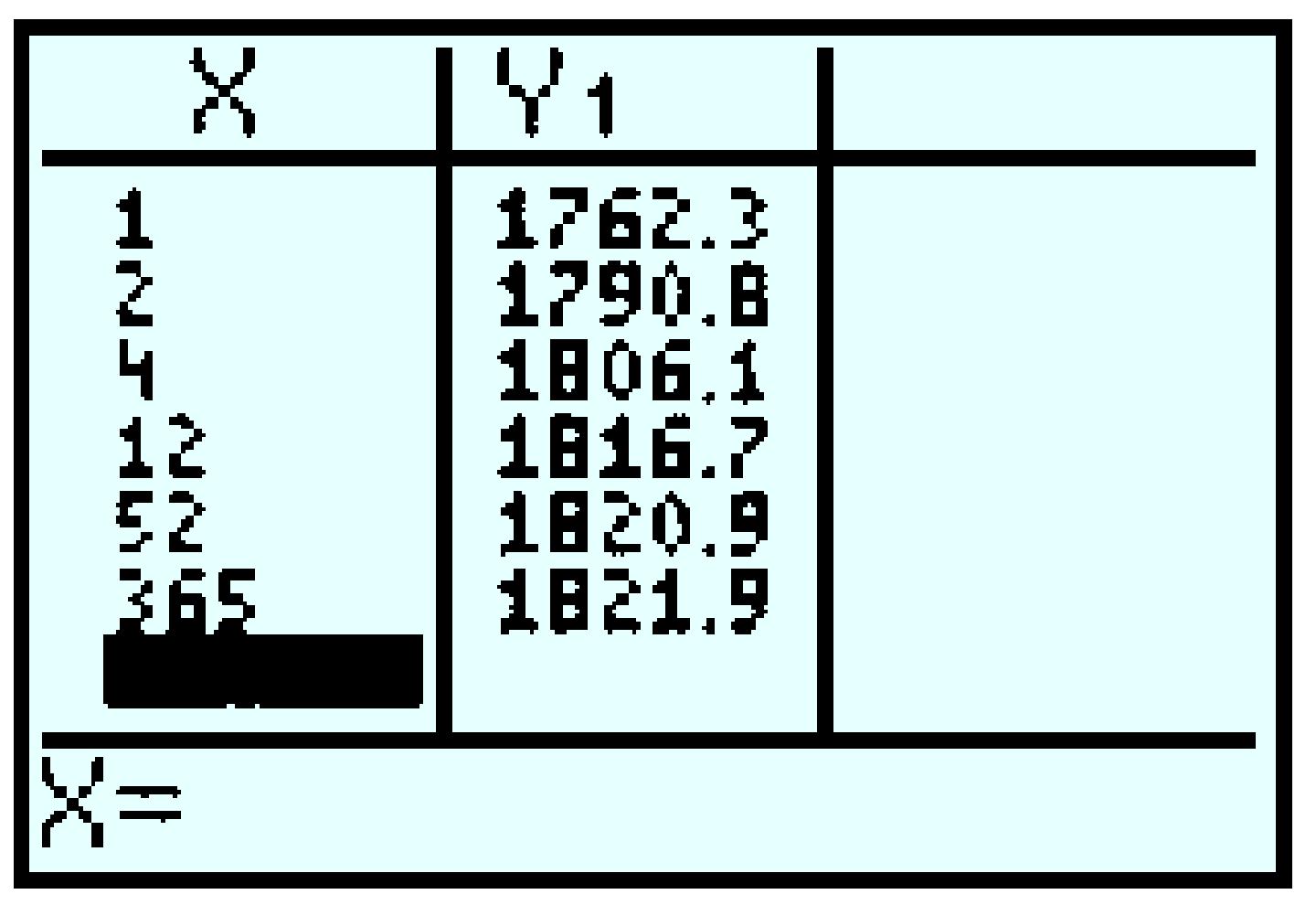
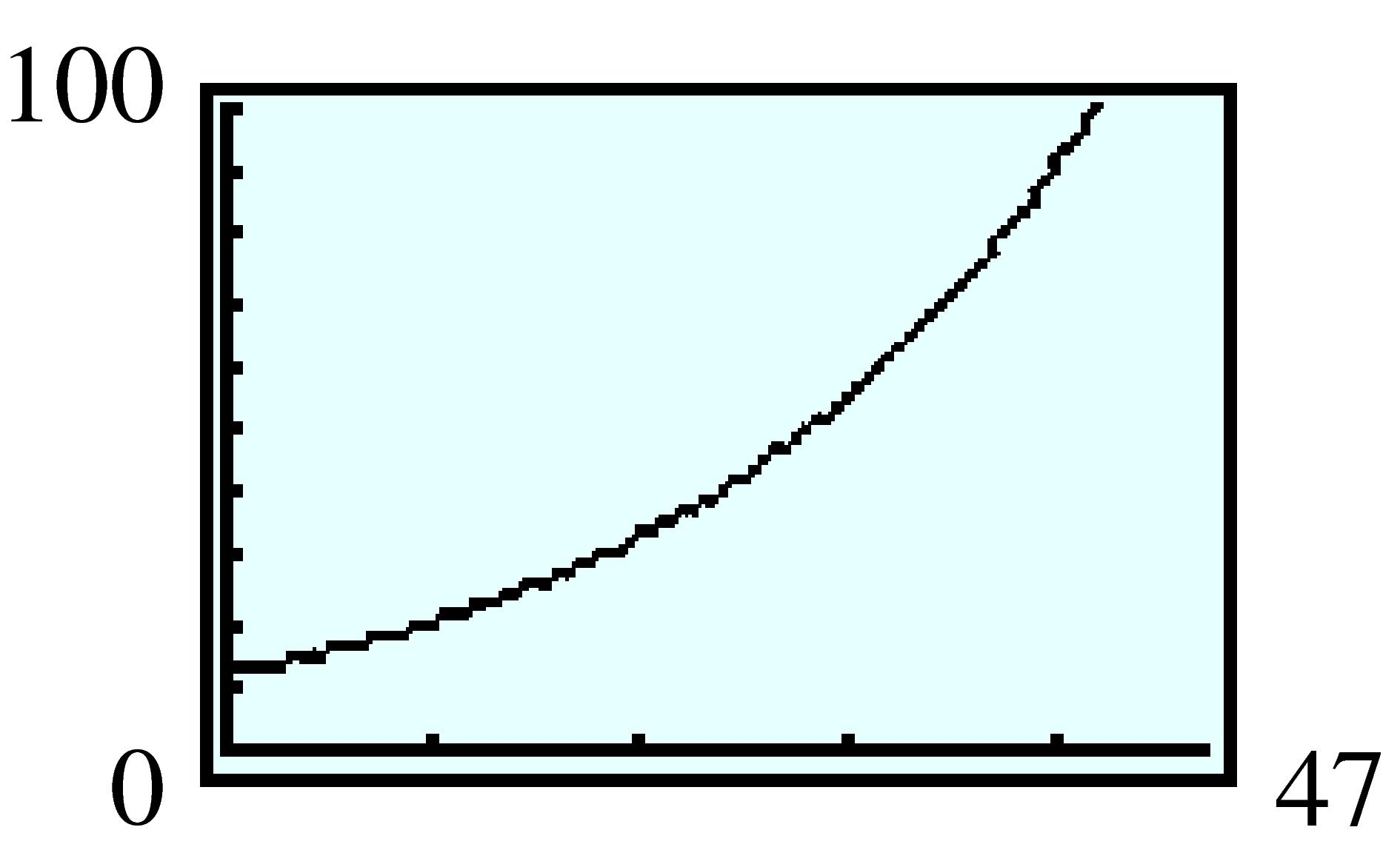
The given model has a smaller growth factor, $1.356\text{,}$ than $2^{1/1.5}\approx 1.59\text{.}$

Name of chip	Year	Moore’s law	$N(t)$	Actual number
Pentium IV	$2000$	$2,306,867,200$	$20,427,413$	$42,000,000$
Pentium M (Banias)	$2003$	$9,227,468,800$	$50,932,200$	$77,000,000$
Pentium M (Dothan)	$2004$	$14,647,693,680$	$69,064,063$	$140,000,000$

About $2.3$ years

4.6 Chapter Summary and Review
Chapter 4 Review Problems

1.

Answer.

$\displaystyle D = 8(1.5)^{t/5}$
$18\text{;}$ $44$

3.

Answer.

$\displaystyle M = 100(0.85)^t$
$52.2$ mg; $19.7$ mg

5.

Answer.

$16n^{2x+10}$

7.

Answer.

$\dfrac{1}{m^{x+2}} $

9.

Answer.

$g(t)=16(0.85)^t $

11.

Answer.

$f (x) = 500\left(\dfrac{1}{5}\right)^x$

13.

Answer.

$4.8\%$ loss

15.

Answer.

$6\%$ loss

17.

Answer.

$y$-intercept $(0, 6)\text{;}$ asymptote: $y = 0$
$\displaystyle [3.472, 10.368]$

19.

Answer.

$x$-intercept $\left(\frac{\log 3}{\log 2}, 0 \right) \text{;}$ $y$-intercept $(0, -2)\text{;}$ asymptote: $y = -3$
$\displaystyle [-2.875,5]$

21.

Answer.

$\dfrac{-4}{3}$

23.

Answer.

$-11$

25.

Answer.

Not (quite) equivalent
$\displaystyle 2^{1/8}\approx 1.090507733\gt 1.0905 $

27.

Answer.

Equivalent
$\displaystyle \left(\dfrac{1}{3} \right)^{x-2} =\left(\dfrac{1}{3} \right)^{x}\cdot \left(\dfrac{1}{3} \right)^{-2} =\left(\dfrac{1}{3} \right)^{x}\cdot 9 $

29.

Answer.

$\displaystyle y = 4 + 2^{x+1}$
Shift the graph of $f~~1$ unit left, $4$ units up.

31.

Answer.

$\displaystyle y = 6 - 3\cdot 2^{x}$
Scale vertically by $3\text{,}$ reflect about $x$-axis, shift $6$ units up.

33.

Answer.

$g$ eventually grows faster.

35.

Answer.

$2^{1.5}\approx 2.83\text{;}$ $2.25$

37.

Answer.

$M = M_0(2)^{t/10}\text{,}$ where $M$ is the organic content, $M_0$ is the organic content at $0\degree$C, and $t$ is the temperature in $\degree$ Celsius.

39.

Answer.

$4$

41.

Answer.

$-1$

43.

Answer.

$-3$

45.

Answer.

$\log_{0.3}(x + 1) = -2$

47.

Answer.

$\dfrac{\log 5.1}{1.3}\approx 0.5433 $

49.

Answer.

$\dfrac{\log (2.9/3)}{-0.7}\approx 0.21 $

51.

Answer.

$\log_b x + \dfrac{1}{3} \log_b y - 2 \log_b z$

53.

Answer.

$\dfrac{4}{3} \log x -\dfrac{1}{3} \log y$

55.

Answer.

$\log\sqrt[3] {\dfrac{x}{y^{2}}} $

57.

Answer.

$\log {\dfrac{1}{8}} $

59.

Answer.

$\dfrac{\log 63}{\log 3}\approx 3.77 $

61.

Answer.

$\dfrac{\log 50}{-0.3\log 6}\approx -7.278 $

63.

Answer.

$\dfrac{\log(N/N_0)}{k}$

65.

Answer.

$\displaystyle 238$
$\displaystyle 2010$

67.

Answer.

$\displaystyle C = 90(1.06)^t$
$$94.48$
$5$ years

69.

Answer.

$7.4$ years
$\displaystyle 6.1\%$

71.

Answer.

$f(x)\approx 1600(1.035)^x $

73.

Answer.

$g(x)\approx 600(0.075)^x $

75.

Answer.

$\dfrac{\log 2}{\log 1.001}\approx 693 $ years
$105$ years

77.

Answer.

$17\%$

79.

Answer.

$$2192.78$

81.

Answer.

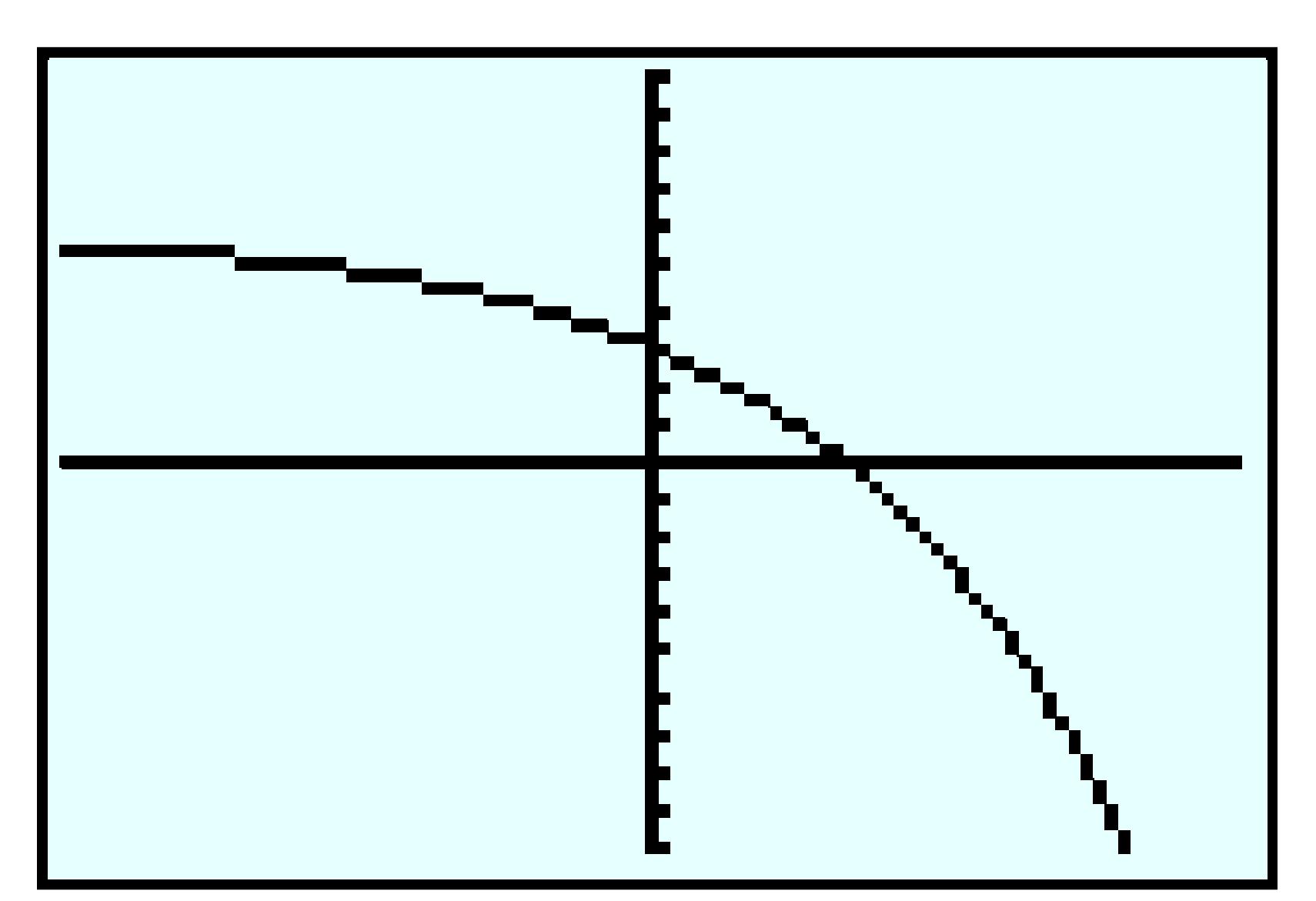
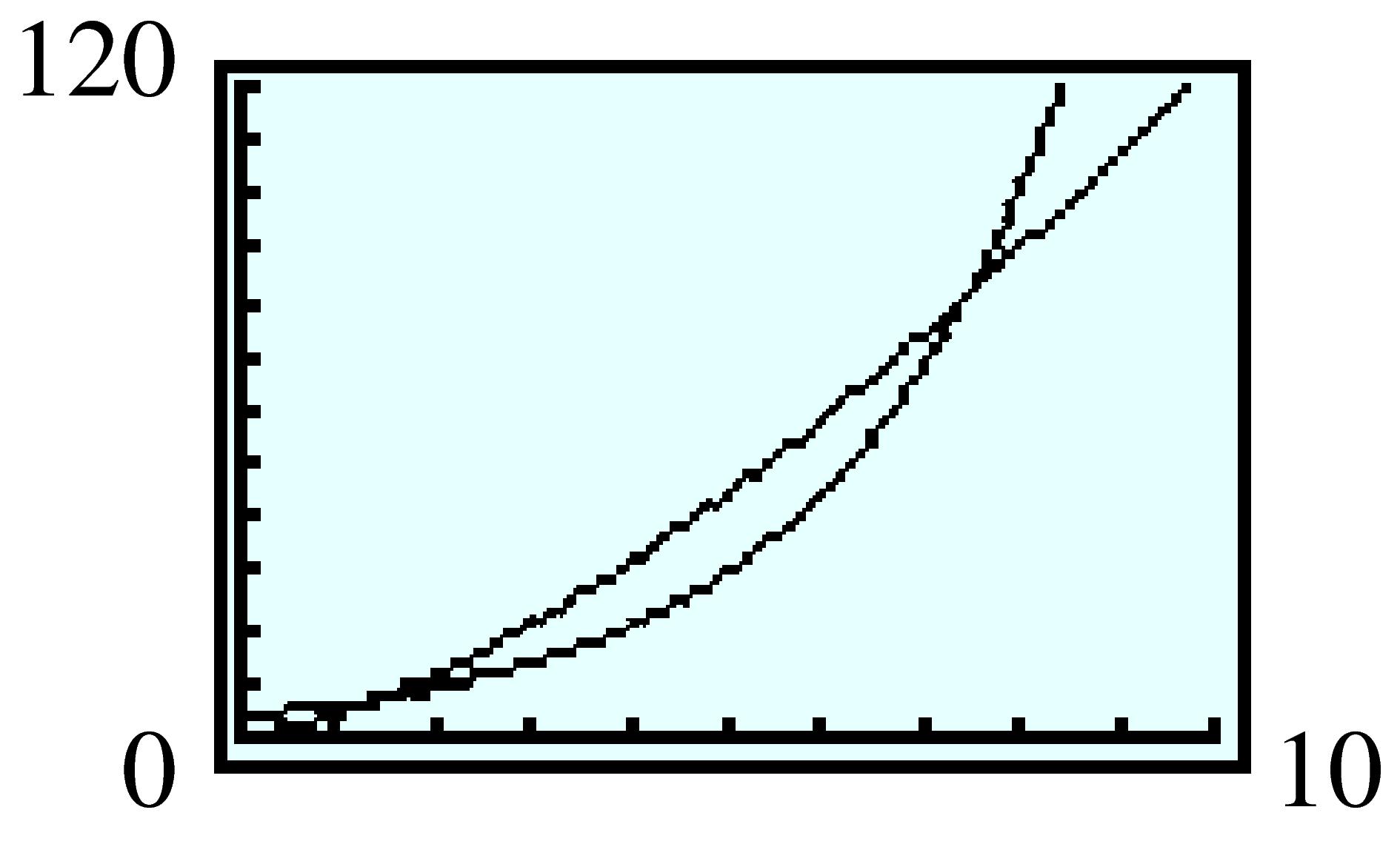
Day $1$ $2$ $3$ $\cdots$ $t$ $\cdots$ $30$

Wage (cent) $2$ $4$ $8$ $\cdots$ $2^t$ $\cdots$ $2^{30}$
$W(t)=2^t$ cents
$$327.68\text{;}$ $$10,737,418.24$

5 Logarithmic Functions
5.1 Inverse Functions
Homework 5.1

1.

Answer.

$x$ $-1$ $0$ $1$ $2$

$f(x)$ $0$ $1$ $-2$ $-1$

$y$ $0$ $1$ $-2$ $-1$

$f^{-1}(y) $ $-1$ $0$ $1$ $2$
$\displaystyle f^{-1}(1)=0 $
$\displaystyle f^{-1}(-1)=2 $

3.

Answer.

$x$ $-1$ $0$ $1$ $2$

$f(x)$ $-1$ $1$ $3$ $11$

$y$ $-1$ $1$ $3$ $11$

$f^{-1}(y) $ $-1$ $0$ $1$ $2$
$\displaystyle f^{1}(1)=0 $
$\displaystyle f^{-1}(3)=1 $

5.

Answer.

$f (60)\approx 38\text{.}$ The car that left the $60$-foot skid marks was traveling at $38$ mph.
$f^{-1} (60) \approx 150\text{.}$ The car traveling at $60$ mph left $150$-foot skid marks

7.

Answer.

$\displaystyle (60~ \text{hours}, 78~ \text{grams})$
$f^{-1} (90) \approx 19\text{,}$ so that the vampire bat’s weight has dropped to $90$ grams about $19$ hours after its last meal.

9.

Answer.

$g (0.05) = 0.28\text{.}$ At $5\%$ interest, $\$1$ earns $\$0.28$ interest in $5$ years.
$\displaystyle 8.45\%$
$\displaystyle g^{-1} (I ) = (I + 1)^{1/5} -1$
$\displaystyle g^{-1} (0.50)\approx 0.0845$

11.

Answer.

$f(0.5) \approx 62.9\text{.}$ At an altitude of $0.5$ miles, you can see $62.9$ miles to the horizon.
$0.0126$ mile, or $66.7$ feet
$\displaystyle h = f^{-1}(d) =\dfrac{d^2}{7920} $
$\displaystyle f^{-1} (10)\approx 0.0126$

13.

Answer.

$\displaystyle h^{-1} (3)\approx -4$
$h^{-1} (x)= 5 - x^2\text{;}$ $~ h^{-1} (3) = -4$

15.

Answer.

$\displaystyle f^{-1} (y) = 3 \sqrt[3]{y} + 2$
$\displaystyle f^{-1} ( f (4)) = f^{-1} (8) = 4$
$\displaystyle f ( f^{-1} (-8)) = f (0) = -8$

17.

Answer.

$6$

19.

Answer.

$\dfrac{2}{9} $

21.

Answer.

$4 $

23.

Answer.

$x$ $0$ $6$

$y$ $300$ $1200$
$x$ $300$ $1200$

$y$ $0$ $6$

25.

Answer.

$x$ $0$ $1$ $2$

$y$ $5$ $20$ $100$
$x$ $5$ $20$ $100$

$y$ $0$ $1$ $2$

27.

Answer.

$\displaystyle f^{-1}(x)=\dfrac{x+6}{2} $

29.

Answer.

$\displaystyle f^{-1}(x)=\sqrt[3]{x-1} $

31.

Answer.

$\displaystyle f^{-1}(x)=\dfrac{1}{x}+1 $

33.

Answer.

Domain: $(-\infty, 4]\text{;}$ Range: $[0,\infty)$
$\displaystyle g^{-1}(x)=4-x^2 $
Domain: $[0,\infty)\text{;}$ Range: $(-\infty,4]$

35.

Answer.

(a) and (d)

37.

Answer.

(a)

39.

Answer.

(a)

41.

Answer.

(a) and (b)

43.

Answer.

$f(x)=4+2x \text{;}$ IV
$f(x)=2-\dfrac{x}{2} \text{;}$ III
$f(x)=-4-2x \text{;}$ I
$f(x)=\dfrac{x}{2} \text{;}$ II

45.

Answer.

5.2 Logarithmic Functions
Homework 5.2

1.

Answer.

$x$ $-1$ $0$ $1$ $2$

$2^x$ $\frac{1}{2} $ $1$ $2$ $4$

$x$ $\frac{1}{2} $ $1$ $2$ $4$

$\log_2 x$ $-1$ $0$ $1$ $2$

3.

Answer.

$x$ $-2$ $-1$ $0$ $1$

$\left(\frac{1}{3}\right)^x$ $9$ $3$ $1$ $\frac{1}{3} $

$x$ $9$ $3$ $1$ $\frac{1}{3} $

$\log_{1/3} x$ $-2$ $-1$ $0$ $1$

5.

Answer.

$\displaystyle x=10,000$
$\displaystyle x=10^{8} $

7.

Answer.

$0\lt x \lt 0.01$

9.

Answer.

$\displaystyle \log 100,322\approx 5.001$
$\displaystyle \log 693\approx 2.841$

11.

Answer.

$\log (-7)$ is undefined.
$\displaystyle 6 \log 28\approx 8.683$

13.

Answer.

$\displaystyle 15.614$
$\displaystyle 0.419$

15.

Answer.

$\displaystyle 81$
$\displaystyle 4$
Definition of logarithm base $3$
$\displaystyle 1.8$
$\displaystyle a$

17.

Answer.

$\displaystyle 2^8$
$\displaystyle -2$

19.

Answer.

$\displaystyle 2k$
$\displaystyle x^3$
$\displaystyle \sqrt{x} $
$\displaystyle 2m$

21.

Answer.

$\displaystyle (9,\infty) $
$\displaystyle f^{-1} (x) = 3^{x-4} + 9 $

23.

Answer.

$\displaystyle f^{-1}(x)= \log_4 (100 - x) - 2 $
$\displaystyle f^{-1} (f(1)) = f^{-1}(36)=\log_4(64)-2=1 $
$\displaystyle f\left(f^{-1} (84)\right)= f (0) = 100 - 4^2 = 84$

25.

Answer.

27.

Answer.

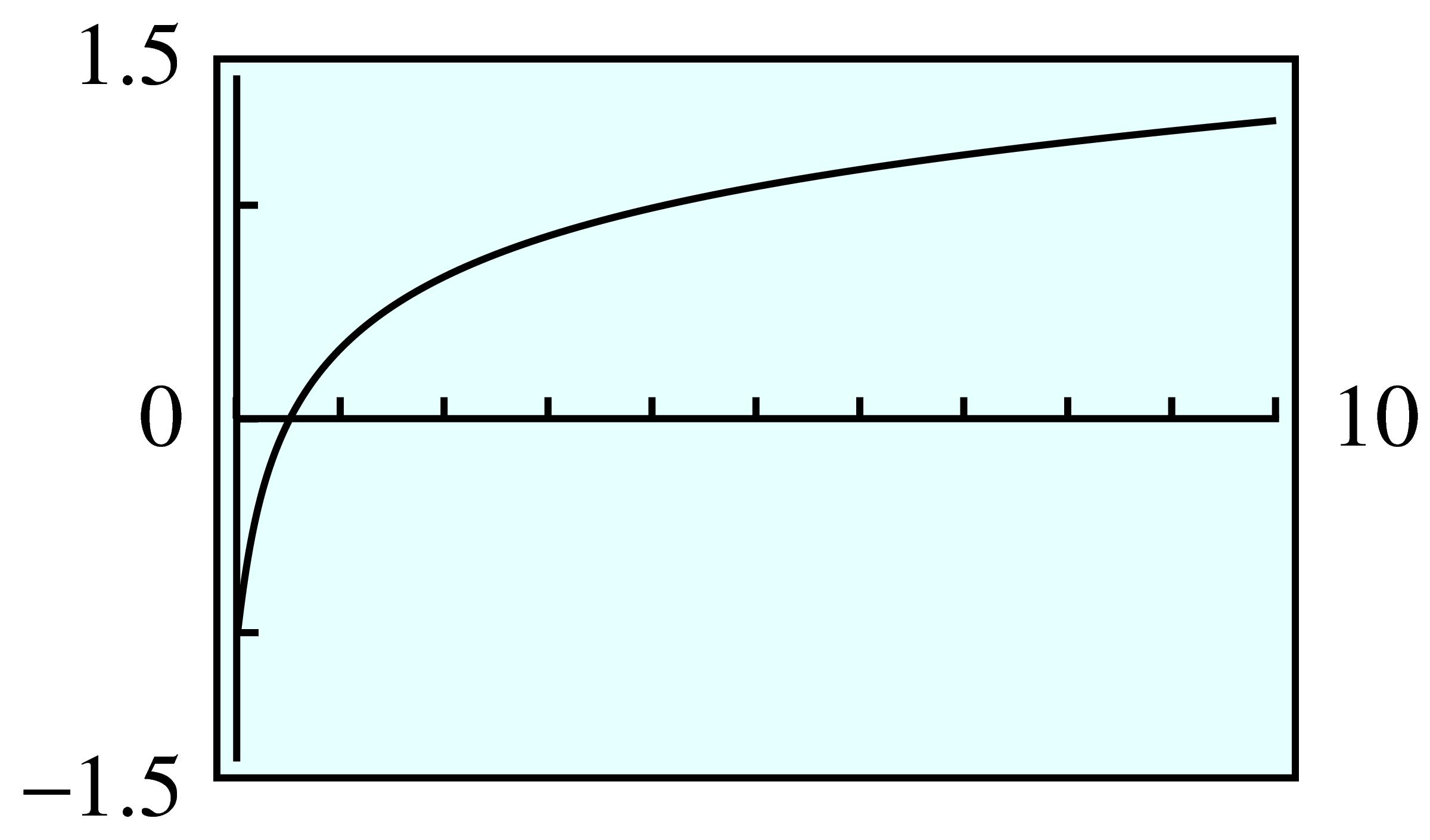
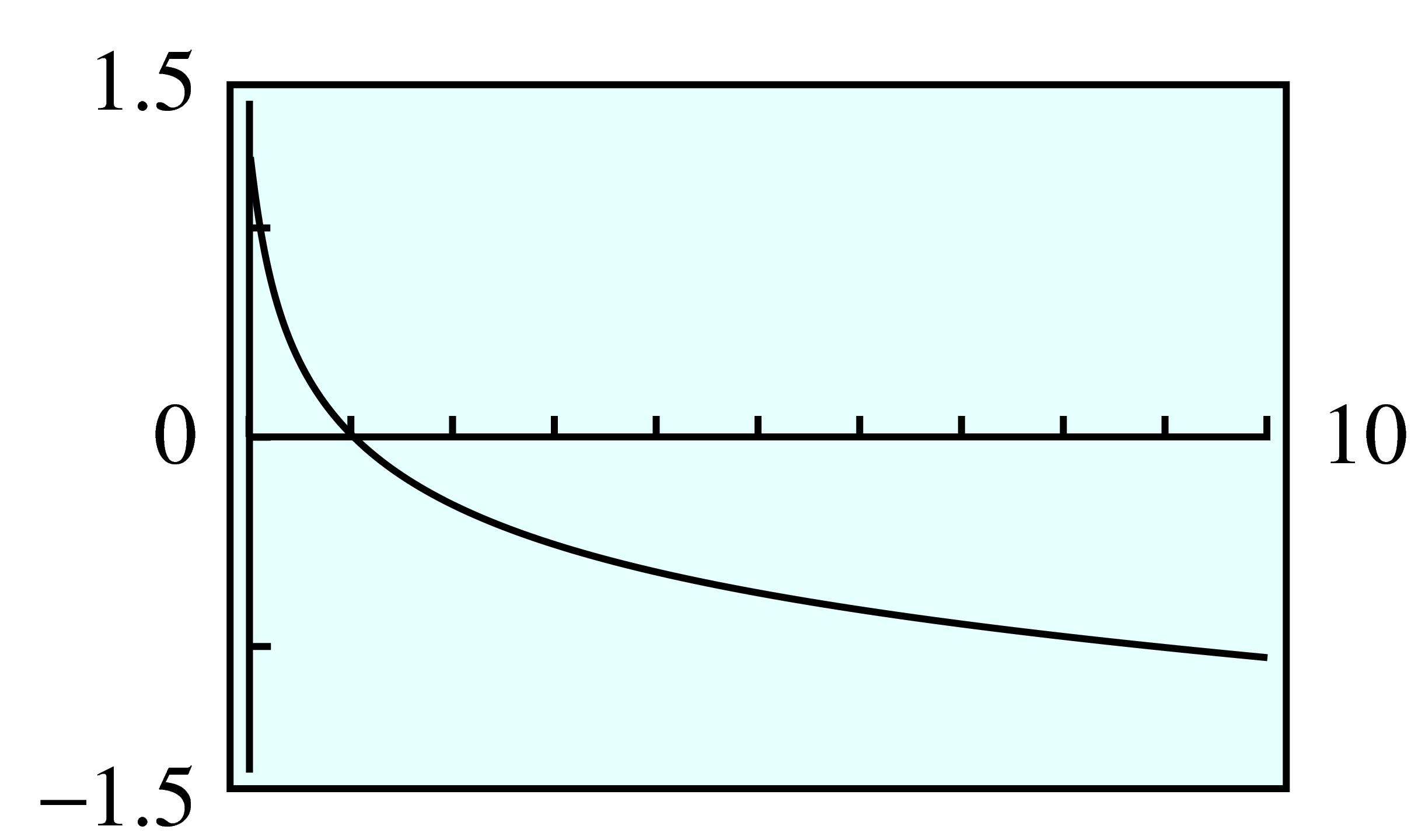
The graph resembles a logarithmic function. The (translated) log function is close to the points but appears too steep at first and not steep enough after $n = 15\text{.}$ Overall, it is a good fit.
$f$ grows (more and more slowly) without bound. $f$ will eventually exceed $100$ per cent, but no one can forget more than $100\%$ of what is learned.

29.

Answer.

$\displaystyle 10^{1.41}\approx 25.704 $
$\displaystyle 10^{-1.69}\approx 0.020417 $
$\displaystyle 10^{0.52}\approx 3.3113 $

31.

Answer.

$16^w = 256$

33.

Answer.

$b^{-2} = 9$

35.

Answer.

$10^{-2.3} = A$

37.

Answer.

$u^{w} = v$

39.

Answer.

$b=2$

41.

Answer.

$b=100$

43.

Answer.

$x=11$

45.

Answer.

$x=7^{2/3} $

47.

Answer.

$x=4$

49.

Answer.

$x=11$

51.

Answer.

$x=3$

53.

Answer.

No solution

55.

Answer.

$A=k(10^{t/T}-1) $

57.

Answer.

$s=\dfrac{b^{N/N_0}}{k} $

59.

Answer.

$H=(H_0)^{kM^2} $

61.

Answer.

63.

Answer.

No inverse function
No inverse function

65.

Answer.

The functions are equal.

67.

Answer.

The functions are equal.

69.

Answer.

$x$	$x^2$	$\log_{10}x$	$\log_{10}x^2 $
$1$	$1$	$0$	$0$
$2$	$4$	$0.301$	$0.602$
$3$	$9$	$0.477$	$0.954$
$4$	$16$	$0.602$	$1.204$
$5$	$25$	$0.699$	$1.398$
$6$	$36$	$0.778$	$1.556$

$\displaystyle \log_{10}x^2=2\log_{10}x $

71.

Answer.

$x$	$y=\log_e x $
$1$	$0$
$2$	$0.693$
$4$	$1.386$
$16$	$2.772$
$\frac{1}{2} $	$-0.693$
$\frac{1}{4} $	$-1.386$
$\frac{1}{16} $	$-2.772$

5.3 The Natural Base
Homework 5.3

1.

Answer.

$x$	$-10$	$-5$	$0$	$5$	$10$	$15$	$20$
$f(x)$	$0.135$	$0.368$	$1$	$2.718$	$7.389$	$20.086$	$54.598$

3.

Answer.

$x$	$-10$	$-5$	$0$	$5$	$10$	$15$	$20$
$f(x)$	$20.086$	$4.482$	$1$	$0.223$	$0.05$	$0.011$	$0.00248$

5.

Answer.

$\displaystyle 2$
$\displaystyle 5t$
$\displaystyle \dfrac{1}{x} $
$\displaystyle \dfrac{1}{2} $

7.

Answer.

$\displaystyle 0.64$
$\displaystyle 3.81$
$\displaystyle -1.20$

9.

Answer.

$\displaystyle 4.14$
$\displaystyle 1.88$
$\displaystyle 0.07$

11.

Answer.

$\displaystyle N(t)=6000e^{0.04t} $
$t$ $0$ $5$ $10$ $15$ $20$ $25$ $30$

$N(t)$ $6000$ $7328$ $8951$ $10,933$ $13,353$ $16,310$ $19,921$
$\displaystyle 15,670$
$70.3$ hrs

13.

Answer.

$941.8$ lumens
$2.2$ cm

15.

Answer.

$P (t) = 20\left(e^{0.4} \right)^t \approx 20\cdot 1.492^t\text{;}$ increasing; initial value $20$

17.

Answer.

$P (t) = 6500\left(e^{-2.5} \right)^t \approx 6500\cdot 0.082^t\text{;}$ decreasing; initial value $6500$

19.

Answer.

$x$ $0$ $0.5$ $1$ $1.5$ $2$ $2.5$

$e^x$ $1 $ $1.6487$ $2.7183$ $4.4817$ $7.3891$ $12.1825$
Each ratio is $e^{0.5} \approx 1.6487\text{:}$ Increasing $x$-values by a constant $\Delta x = 0.5$ corresponds to multiplying the $y$-values of the exponential function by a constant factor of $e^{\Delta x}\text{.}$

21.

Answer.

$x$ $0$ $0.6931$ $1.3863$ $2.0794$ $2.7726$ $3.4657$ $4.1589$

$e^x$ $1 $ $2$ $4$ $8$ $16$ $32$ $64$
Each difference in $x$-values is approximately $\ln 2\approx 0.6931\text{:}$ Increasing $x$-values by a constant $\Delta x = \ln 2$ corresponds to multiplying the $y$-values of the exponential function by a constant factor of $e^{\Delta x} = e^{\ln 2} = 2\text{.}$ That is, each function value is approximately equal to double the previous one.

23.

Answer.

$0.8277$

25.

Answer.

$-2.9720$

27.

Answer.

$1.6451$

29.

Answer.

$-3.0713$

31.

Answer.

$t=\dfrac{1}{k}\ln y $

33.

Answer.

$t=\ln \left(\dfrac{k}{k-y}\right) $

35.

Answer.

$k=e^{T/T_0}-10 $

37.

Answer.

$n$ $0.39$ $3.9$ $39$ $390$

$\ln n$ $-0.942 $ $1.361 $ $3.664 $ $5.966 $
Each difference in function values is approximately $\ln 10\approx 2.303\text{:}$ Multiplying $x$-values by a constant factor of $10$ corresponds to adding a constant value of ln 10 to the $y$-values of the natural log function.

39.

Answer.

$n$ $2$ $4$ $8$ $16$

$\ln n$ $0.693 $ $1.386 $ $2.079 $ $2.773 $
Each quotient equals $k\text{,}$ where $n = 2^k\text{.}$ Because $\ln n = \ln 2^k = k\cdot \ln 2\text{,}$ $k = \dfrac{\ln n}{\ln 2}\text{.}$

41.

Answer.

$\displaystyle N (t) = 100e^{(\ln 2)t}\approx 100e^{0.6931t}$

43.

Answer.

$\displaystyle N (t) = 1200e^{(\ln 0.6)t}\approx 1200e^{-0.5108t}$

45.

Answer.

$\displaystyle N (t) = 10e^{(\ln 1.15)t}\approx 10e^{0.1398t}$

47.

Answer.

$\displaystyle 20,000$
$\displaystyle \left(\dfrac{35,000}{20,000} \right)^{1/10}\approx e^{0.056} $
$\displaystyle P(t) = 20,000e^{0.056t} $
$\displaystyle 107,188$

49.

Answer.

$\displaystyle \left(\dfrac{385}{500} \right)^{1/2}\approx e^{-0.1307} $
$\displaystyle N(t) = 500e^{-0.1307t} $
$135.3$ mg

51.

Answer.

$\displaystyle A(t) = 500e^{0.095t}$
$7.3$ years
$7.3$ years

d–e

53.

Answer.

$6$ hours
$6$ hours

55.

Answer.

$\frac{1}{2}N_0 \text{,}$ $\frac{1}{4}N_0 \text{,}$ $\frac{1}{16}N_0$
$\displaystyle N (t) = N_0e^{-0.0866t}$

57.

Answer.

$\displaystyle y = 116 (0.975)^t$
$\displaystyle G (t) = 116e^{-0.025t}$
$28$ minutes

5.4 Logarithmic Scales
Homework 5.4

1.

Answer.

3.

Answer.

5.

Answer.

$1.58\text{,}$ $6.31\text{,}$ $15.8\text{,}$ $63.1$

7.

Answer.

$1\text{,}$ $80\text{,}$ $330\text{,}$ $1600\text{,}$ $7000\text{,}$ $4\times 10^7$

9.

Answer.

11.

Answer.

Proxima Centauri: $15.5\text{;}$ Barnard: $13.2\text{;}$ Sirius: $1.4\text{;}$ Vega: $0.6\text{;}$ Arcturus: $-0.4\text{;}$ Antares: $-4.7\text{;}$ Betelgeuse: $-7.2$

13.

Answer.

$\displaystyle 1$
$\displaystyle 0.5012$
$\displaystyle 0.1259$
$\displaystyle 0.01$
$\displaystyle 0.000079$
$\displaystyle 3.2\times 10^{-7} $
$\displaystyle 2\times 10^{-8} $
$\displaystyle 8\times 10^{-10} $

15.

Answer.

$\displaystyle 10^{1.75}\approx 56.2341$
$\displaystyle 10^{(\log 600)/2}\approx 24.4949 $

17.

Answer.

$10^{3.4} \approx 2512$

19.

Answer.

A: $a\approx 45\text{,}$ $p \approx 7.4\%\text{;}$ B: $a \approx 400\text{,}$ $p \approx 15\%\text{;}$ C: $a\approx 6000\text{,}$ $p\approx 50\%\text{;}$ D: $a \approx 13000\text{,}$ $p \approx 45\%$

21.

Answer.

$3.2$

23.

Answer.

$0.0126$

25.

Answer.

$100$

27.

Answer.

$6,309,573$ watts per square meter

29.

Answer.

$1000$

31.

Answer.

$12.6$

33.

Answer.

$100$

35.

Answer.

$\approx 25,000$

37.

Answer.

$4.7$

39.

Answer.

$53$

5.5 Chapter Summary and Review
Chapter 5 Review Problems

1.

Answer.

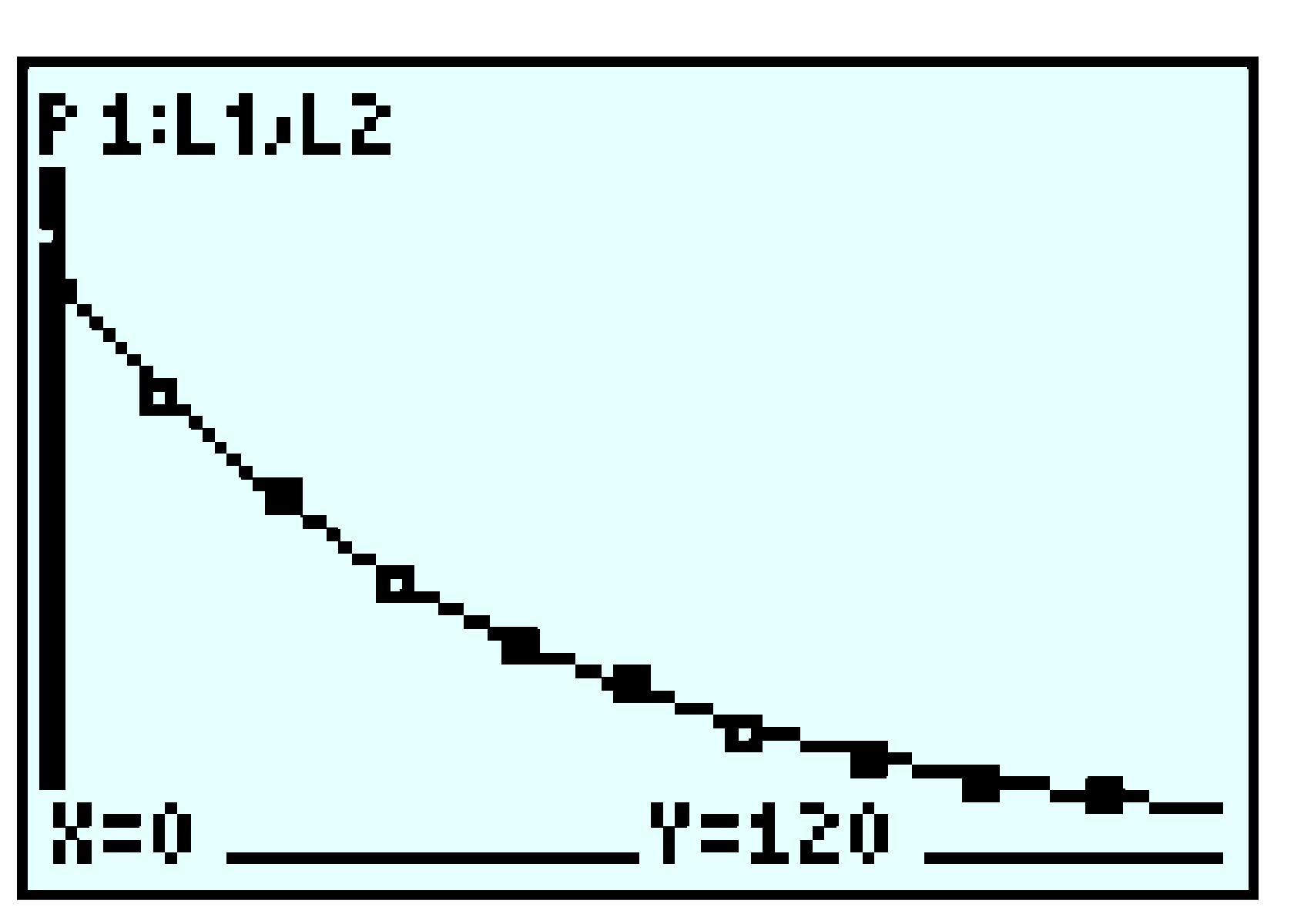
$y$	$-1$	$1$	$3$	$11$
$x=f^{-1}(y)$	$-1$	$0$	$1$	$2$

3.

Answer.

$y$	$0$	$\frac{-1}{3} $	$-1$	$-3$
$w=g^{-1}(y)$	$-1$	$0$	$1$	$2$

5.

Answer.

$\displaystyle P^{-1}(350)=40$
$\displaystyle P^{-1}(100)=0 $

7.

Answer.

$\displaystyle f^{-1} (x) = x - 4$

9.

Answer.

$\displaystyle f^{-1} (x) =\sqrt[3]{x+1} $

11.

Answer.

$\displaystyle f^{-1} (x) =\dfrac{1}{x-2} $

13.

Answer.

$0$

15.

Answer.

$f^{-1} (300) = 200\text{:}$ $\$200,000$ in advertising results in $\$300,000$ in revenue.
$f (A) = 250$ or $A = f^{-1} (250)$

17.

Answer.

$10^z = 0.001$

19.

Answer.

$2^{x-2} = 3$

21.

Answer.

$b^{3} = 3x+1$

23.

Answer.

$n^{p-1} = q$

25.

Answer.

$6n$

27.

Answer.

$2x+6$

29.

Answer.

$-1$

31.

Answer.

$\dfrac{1}{2} $

33.

Answer.

$4 $

35.

Answer.

$\dfrac{-15}{8} $

37.

Answer.

$\dfrac{9}{4} $

39.

Answer.

$3 $

41.

Answer.

$x\approx 1.548 $

43.

Answer.

$x\approx 411.58 $

45.

Answer.

$x\approx 2.286 $

47.

Answer.

$\sqrt{x} $

49.

Answer.

$k-3 $

51.

Answer.

$\displaystyle P = 7,894,862e^{-0.011t}$
$\displaystyle 1.095\%$

53.

Answer.

$$1419.07 $
$13.9$ years
$\displaystyle t = 20 \ln\left(\dfrac{A}{1000} \right)$

55.

Answer.

$t=\dfrac{-1}{k}\ln\left(\dfrac{y-6}{12} \right) $

57.

Answer.

$M=N^{Qt} $

59.

Answer.

$P (t) = 750 (1.3771)^t$

61.

Answer.

$N(t) = 600 e^{-0.9163t}$

63.

Answer.

65.

Answer.

Order $3\text{:}$ $17,000\text{;}$ Order $4\text{:}$ $5000\text{;}$ Order $8\text{:}$ $40\text{;}$ Order $9\text{:}$ $11$

67.

Answer.

$5\times 10^{-7}$

69.

Answer.

$3160$

6 Quadratic Functions
6.1 Factors and $x$-Intercepts
Homework 6.1

1.

Answer.

$t$ $0$ $0.5$ $1$ $1.5$ $2$ $2.5$ $3$ $3.5$ $4$ $4.5$ $5$

$h$ $300$ $306$ $304$ $294$ $276$ $250$ $216$ $174$ $124$ $66$ $0$
$306.25$ ft at $0.625$ sec
$1.25$ sec
$5$ sec

3.

Answer.

$\dfrac{-5}{2} \text{,}$ $~2$

5.

Answer.

$0 \text{,}$ $~\dfrac{-10}{3} $

7.

Answer.

$\dfrac{-3}{4} \text{,}$ $~-8 $

9.

Answer.

$4 $

11.

Answer.

$\dfrac{1}{2} \text{,}$ $~-3$

13.

Answer.

$0 \text{,}$ $~3$

15.

Answer.

$1$

17.

Answer.

$\dfrac{1}{2} \text{,}$ $~1 $

19.

Answer.

$2 \text{,}$ $~3 $

21.

Answer.

$-1 \text{,}$ $~2 $

23.

Answer.

$-3 \text{,}$ $~6 $

25.

Answer.

The 3 graphs have the same $x$-intercepts. In general, the graph of $y = ax^2 + bx + c$ has the same $x$-intercepts as the graph of $y = k(ax^2 + bx + c)\text{.}$

27.

Answer.

The 3 graphs have the same $x$-intercepts. In general, the graph of $y = ax^2 + bx + c$ has the same $x$-intercepts as the graph of $y = k(ax^2 + bx + c)\text{.}$

29.

Answer.

$x^2 + x - 2 = 0$

31.

Answer.

$x^2 + 5x = 0$

33.

Answer.

$2x^2 + 5x - 3 = 0$

35.

Answer.

$8x^2 -10x -3 = 0$

37.

Answer.

$f(x) = 0.1(x - 18)(x + 15)$

39.

Answer.

$g(x) = -0.08(x - 18)(x + 32)$

41.

Answer.

$\displaystyle 10^2 + h^2 = (h + 2)^2$
$24$ ft

43.

Answer.

$\displaystyle h=-16t^2 + 16t + 8$
$12$ ft; $8$ ft
$11=-16t^2+16t+8\text{;}$ at $\dfrac{1}{4} $ sec and $\dfrac{3}{4} $ sec
$\displaystyle \Delta \text{Tbl}=0.25$
$1.37$ sec

45.

Answer.

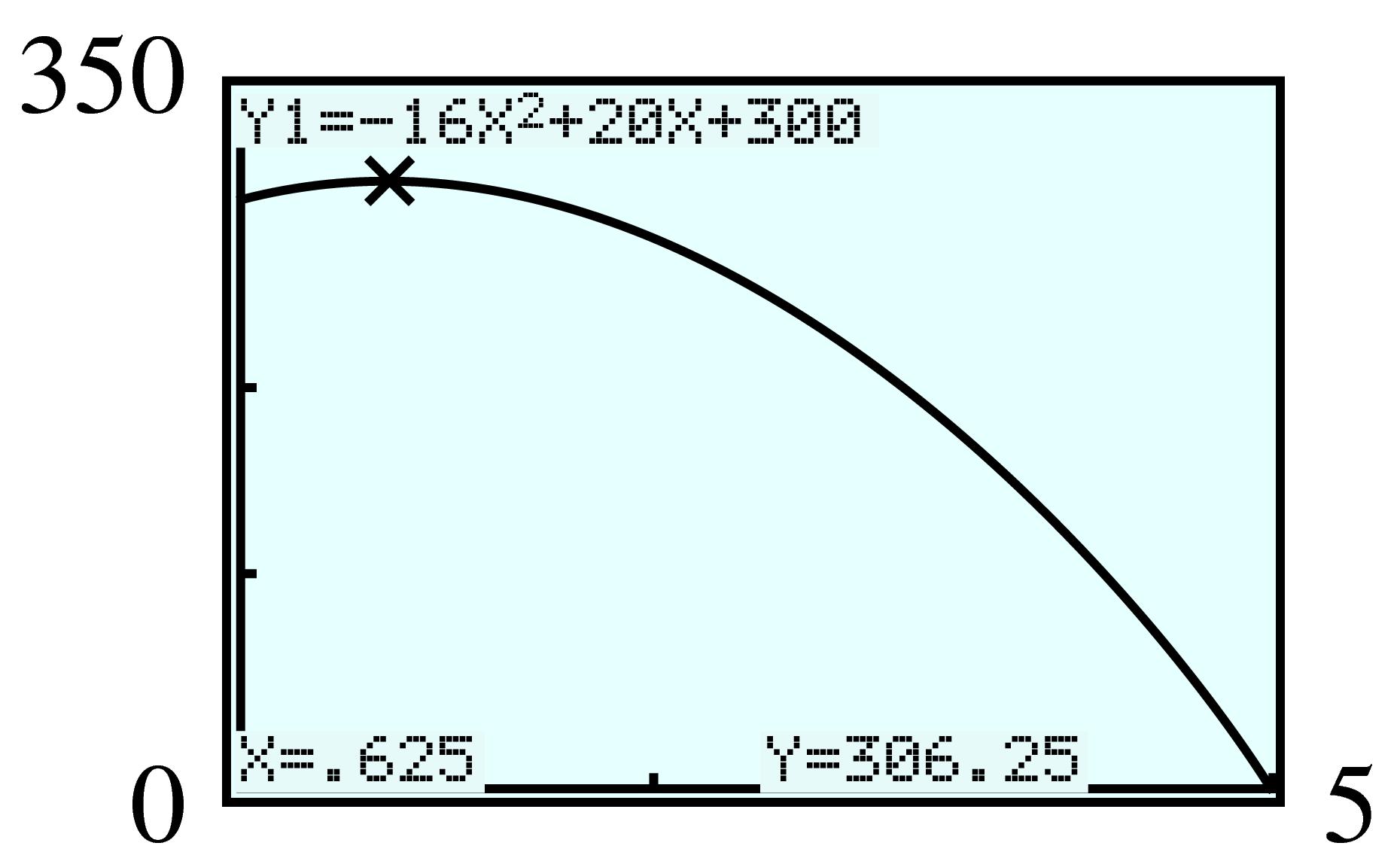
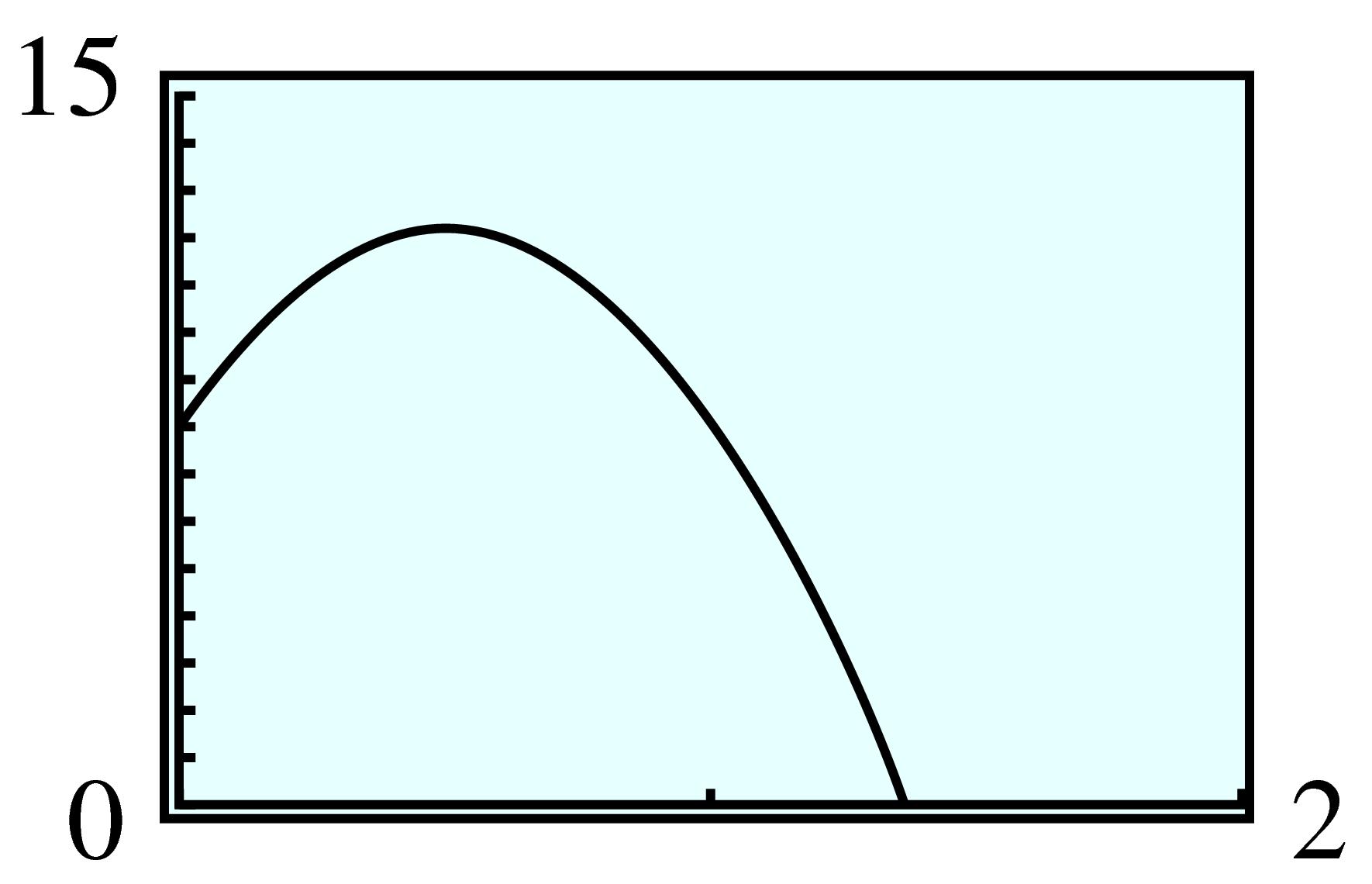
Width	Length	Area
$10$	$170$	$1700$
$20$	$160$	$3200$
$30$	$150$	$4500$
$40$	$140$	$5600$
$50$	$130$	$6500$
$60$	$120$	$7200$
$70$	$110$	$7700$
$80$	$100$	$8000$

$l= 180 - x\text{,}$ $A = 180x - x^2\text{;}$ $80$ yd by $100$ yd
$180x-x^2=8000\text{,}$ $80$ yd by $100$ yd, or $100$ yd by $80$ yd. There are two solutions because the pasture can be oriented in two directions.

47.

Answer.

$l = x - 4\text{,}$ $~w = x - 4\text{,}$ $~h = 2\text{,}$ $~V = 2(x - 4)^2$
$x$ $4$ $5$ $6$ $7$ $8$ $9$ $10$

$V$ $0$ $2$ $8$ $18$ $32$ $50$ $72$
As $x$ increases, $V$ increases.
$9$ inches by $9$ inches.
$2(x - 4)^2 = 50\text{,}$ $~x = 9$

49.

Answer.

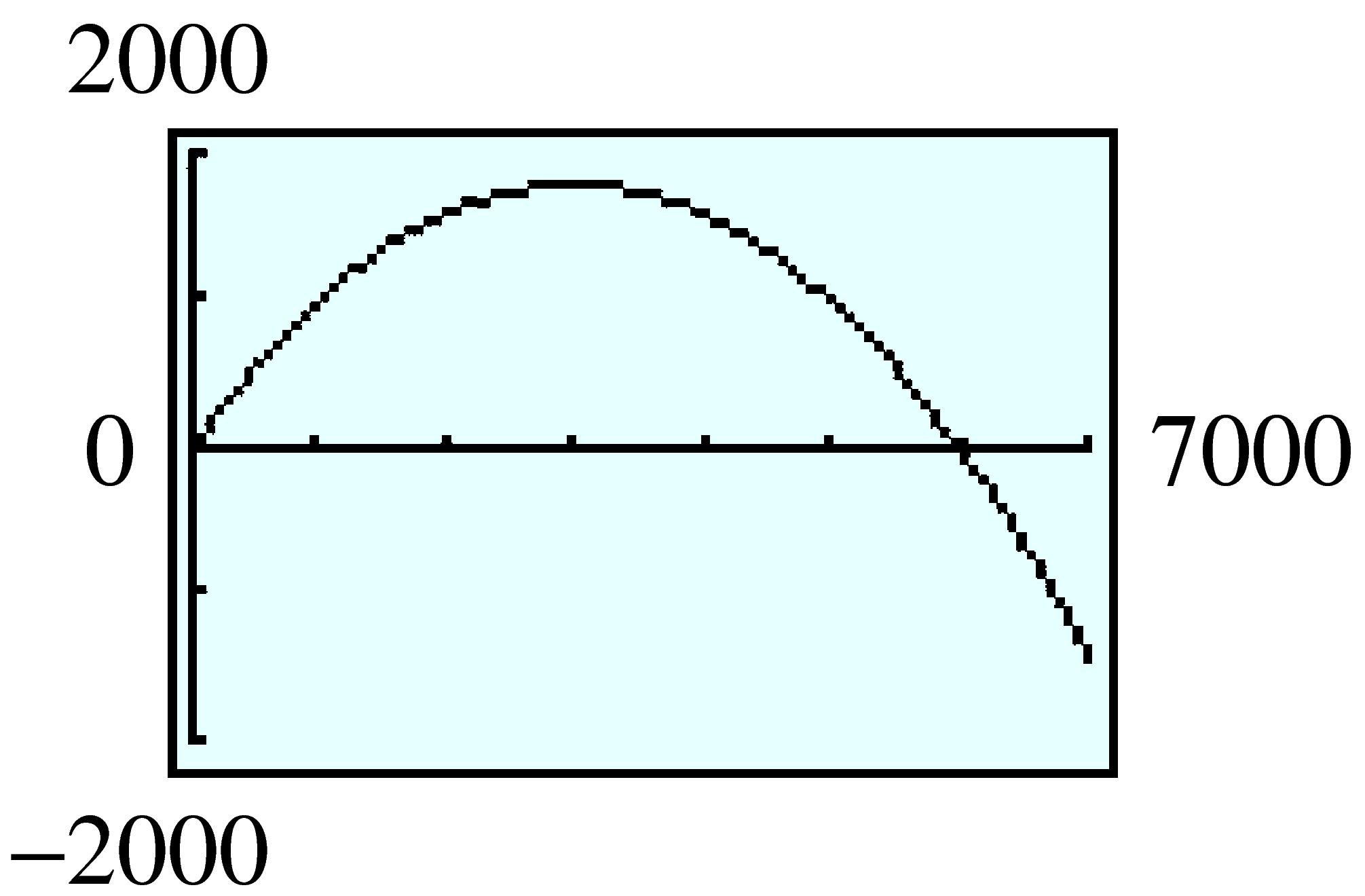
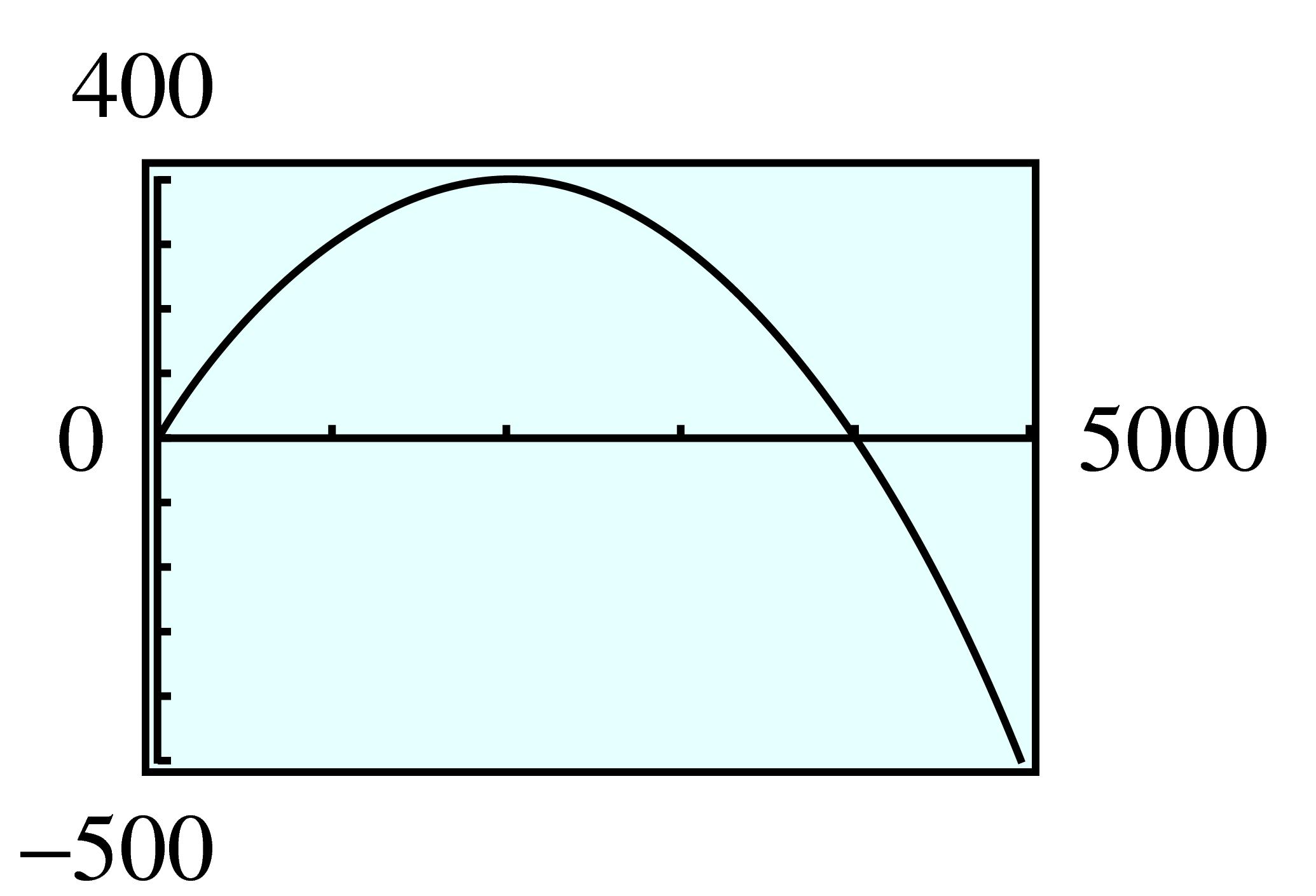
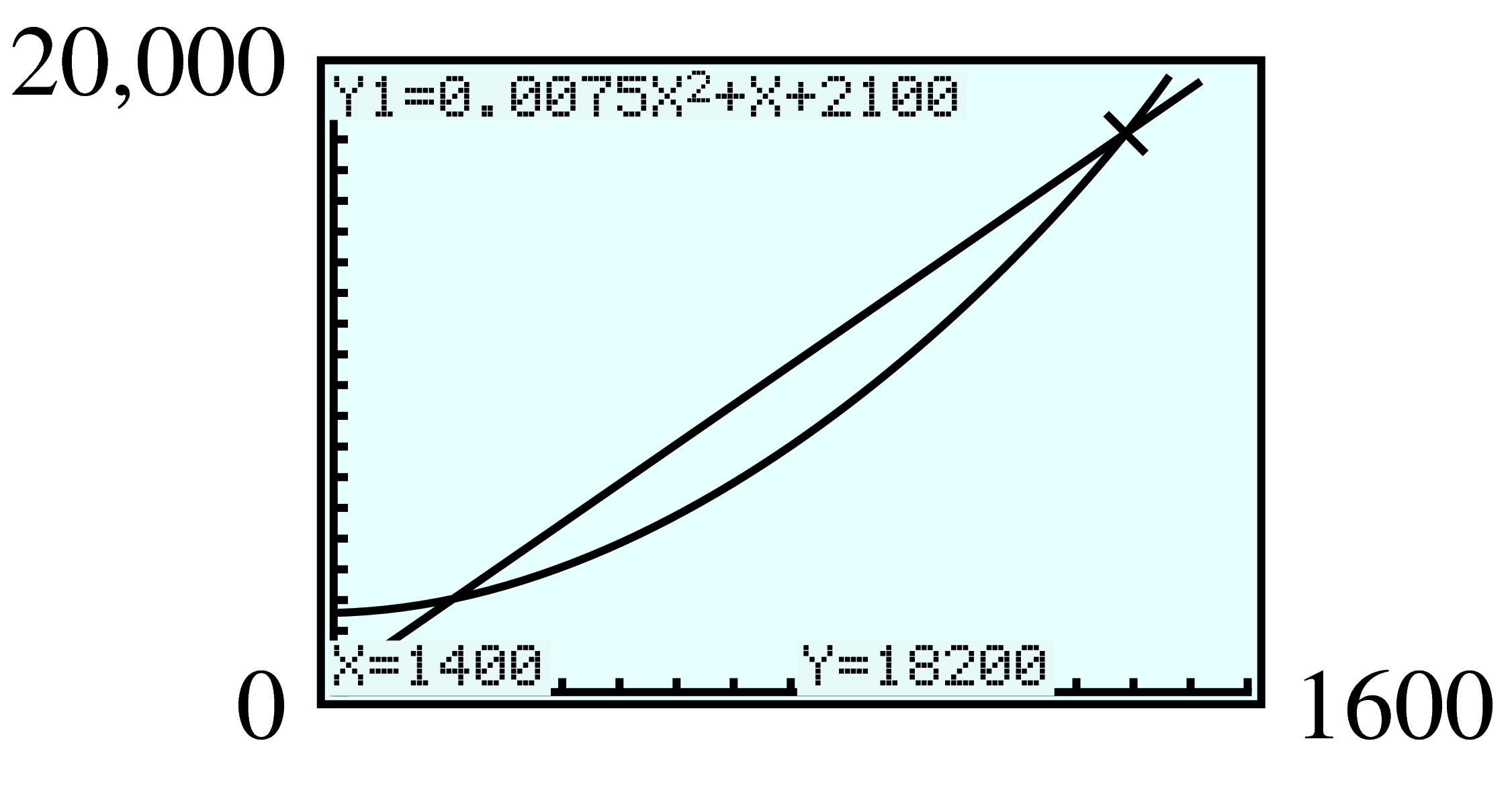
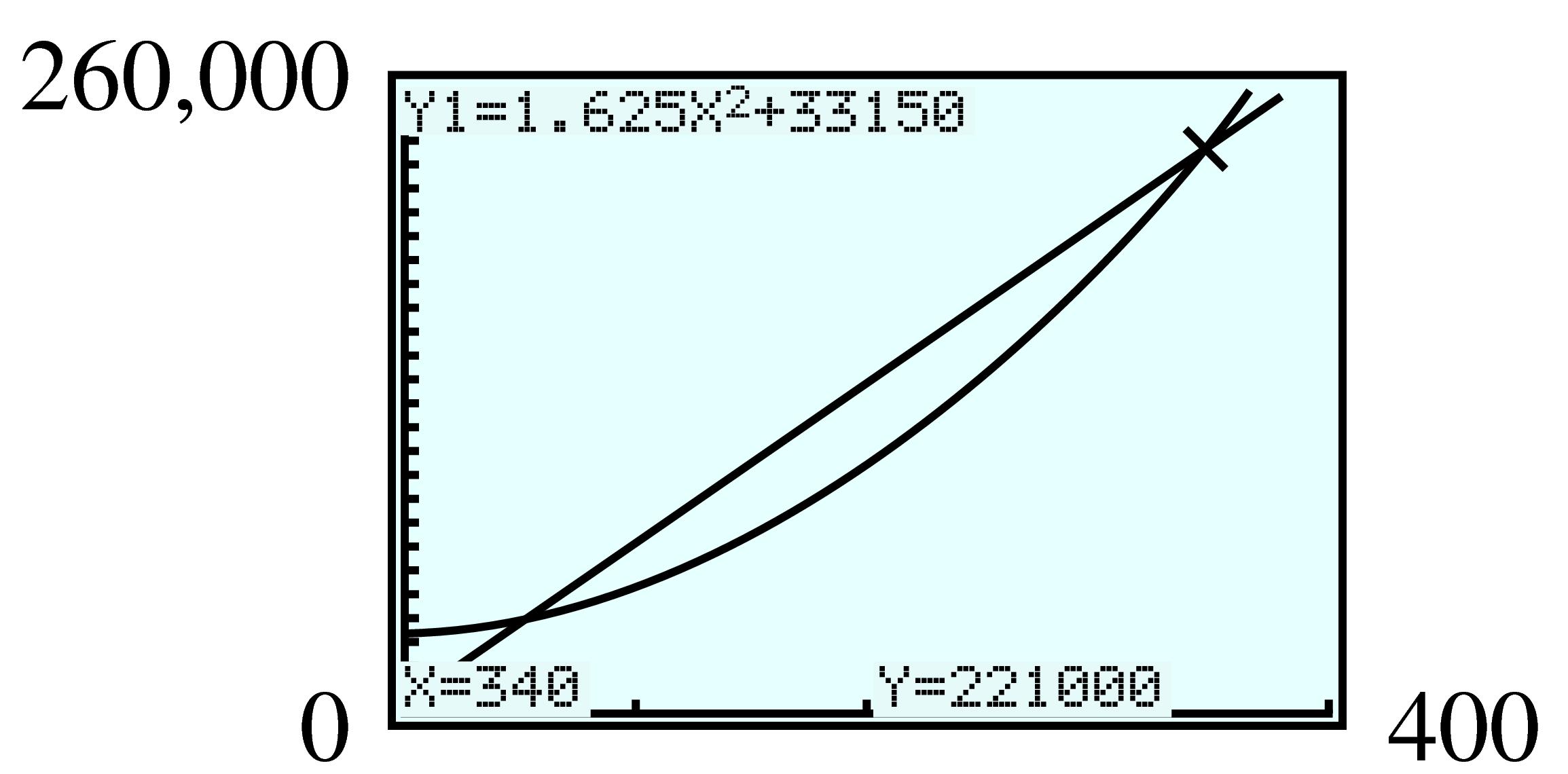
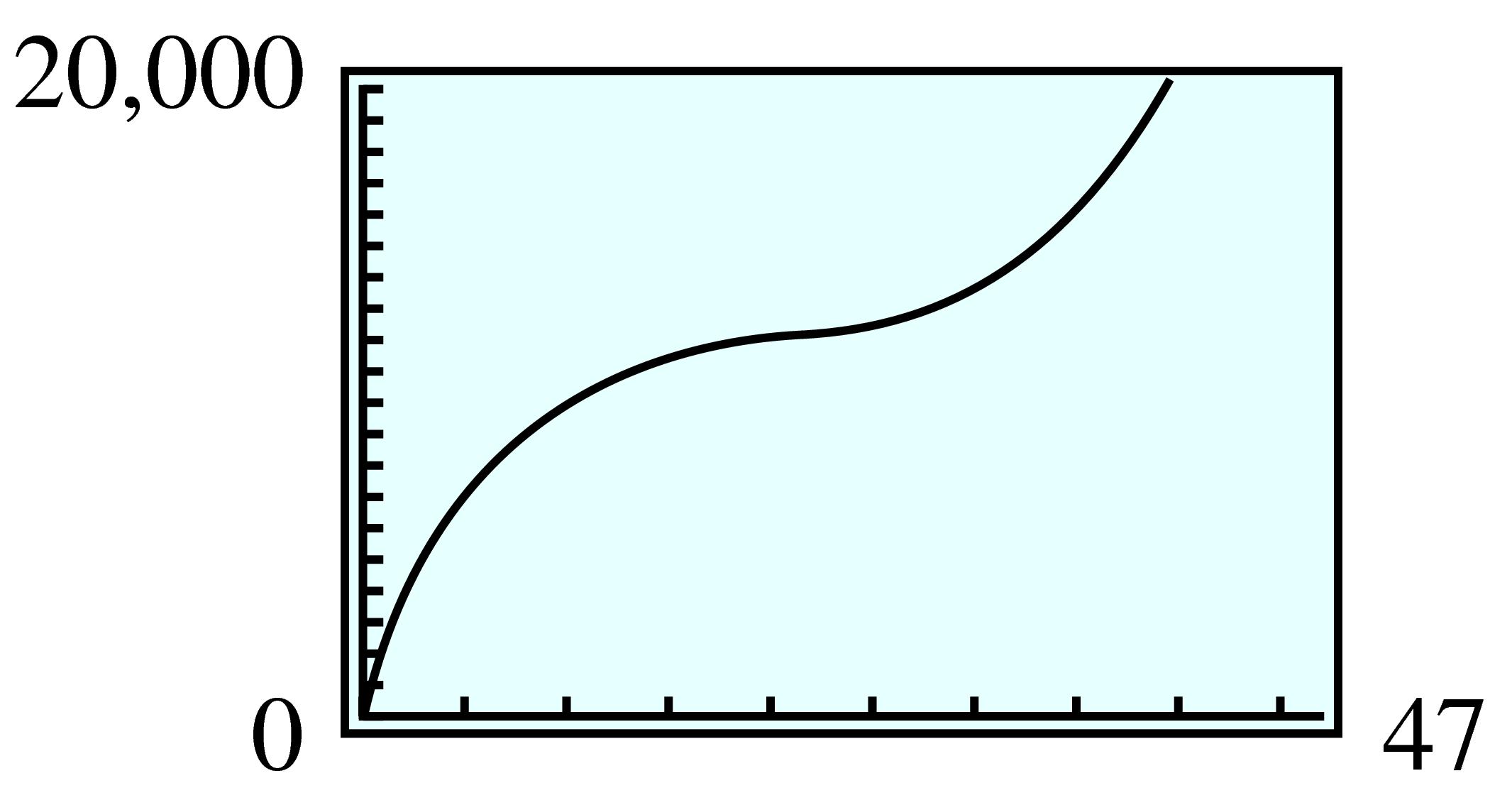
$x$ $0$ $500$ $1000$ $1500$ $2000$ $2500$ $3000$ $3500$

$I$ $0$ $550$ $1000$ $1350$ $1600$ $1750$ $1800$ $1750$

$x$ $4000$ $4500$ $5000$ $5500$ $6000$ $6500$ $7000$

$I$ $1600$ $1350$ $1000$ $550$ $0$ $-650$ $-1400$
$1600\text{,}$ $1000\text{,}$ $-1400$
No increase
$3000\text{;}$ $1800$

51.

Answer.

$\pm 1$

53.

Answer.

$\sqrt[3]{-3/4} \text{,}$ $1$

55.

Answer.

$-27 \text{,}$ $1$

57.

Answer.

$\log 2 \text{,}$ $\log 3$

59.

Answer.

$1 \text{,}$ $2 $

61.

Answer.

$\dfrac{-1}{6} \text{,}$ $1 $

63.

Answer.

$\displaystyle A=\dfrac{1}{2}(x^2-y^2) $
$\displaystyle A=\dfrac{1}{2}(x-y)(x+y)$
$18$ sq ft

6.2 Solving Quadratic Equations
Homework 6.2

1.

Answer.

$\displaystyle (x+4)^2 $
$\displaystyle \left(x-\dfrac{7}{2} \right)^2 $
$\displaystyle \left(x+\dfrac{3}{4} \right)^2 $
$\displaystyle \left(x-\dfrac{2}{5} \right)^2 $

3.

Answer.

$1$

5.

Answer.

$-4\text{,}$ $~-5$

7.

Answer.

$\dfrac{3}{2} \pm \sqrt{\dfrac{21}{4}} = \dfrac{-3\pm\sqrt{21}}{2} $

9.

Answer.

$-1\pm \sqrt{\dfrac{5}{2}} $

11.

Answer.

$\dfrac{-4}{3} \text{,}$ $~1$

13.

Answer.

$\dfrac{1}{4} \pm \sqrt{\dfrac{13}{16}} = \dfrac{1\pm\sqrt{13}}{4} $

15.

Answer.

$-1 \text{,}$ $\dfrac{4}{3} $

17.

Answer.

$-2 \text{,}$ $\dfrac{2}{5} $

19.

Answer.

$-1\pm\sqrt{1-c} $

21.

Answer.

$-\dfrac{b}{2} \pm \sqrt{\dfrac{b^2-4}{4}} = \dfrac{-b\pm\sqrt{b^2-4}}{2} $

23.

Answer.

$\dfrac{-1\pm\sqrt{4a+1}}{a} $

25.

Answer.

$\displaystyle A=(x+y)^2 $
$\displaystyle A=x^2+2xy+y^2$
$x^2\text{,}$ $xy\text{,}$ $xy\text{,}$ $y^2$

27.

Answer.

$1.618\text{,}$ $~-0.618$

29.

Answer.

$1.449\text{,}$ $~-3.449$

31.

Answer.

$1.695\text{,}$ $~-0.295$

33.

Answer.

$1.434\text{,}$ $~0.232$

35.

Answer.

$-5.894\text{,}$ $~39.740$

37.

Answer.

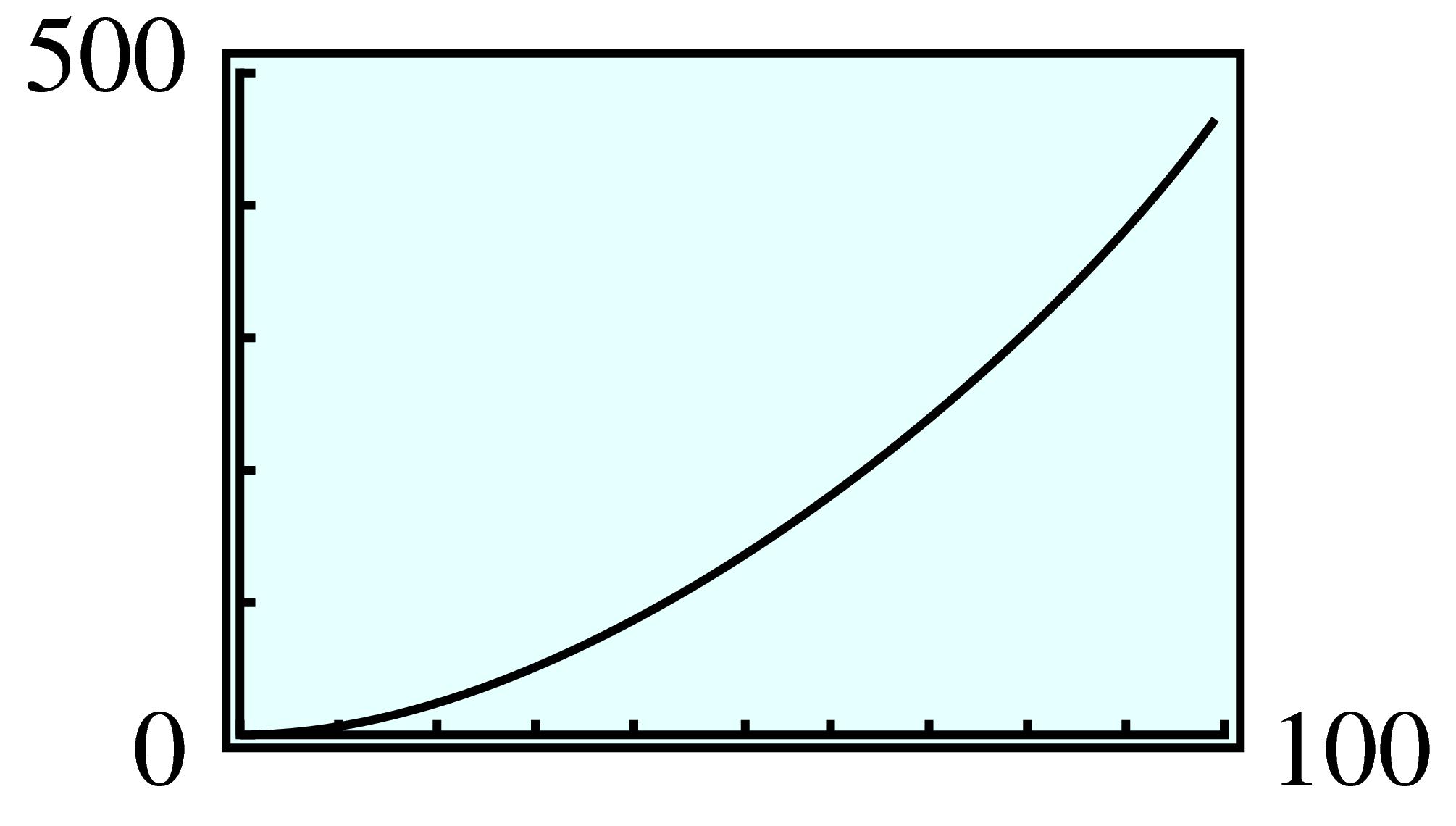
$s$ $10$ $20$ $30$ $40$ $50$ $60$ $70$ $80$ $90$ $100$

$d$ $9$ $27$ $53$ $87$ $129$ $180$ $239$ $307$ $383$ $467$
$\dfrac{s^2}{24}+\dfrac{s}{2}=50\text{;}$ $~29.16$ mph

39.

Answer.

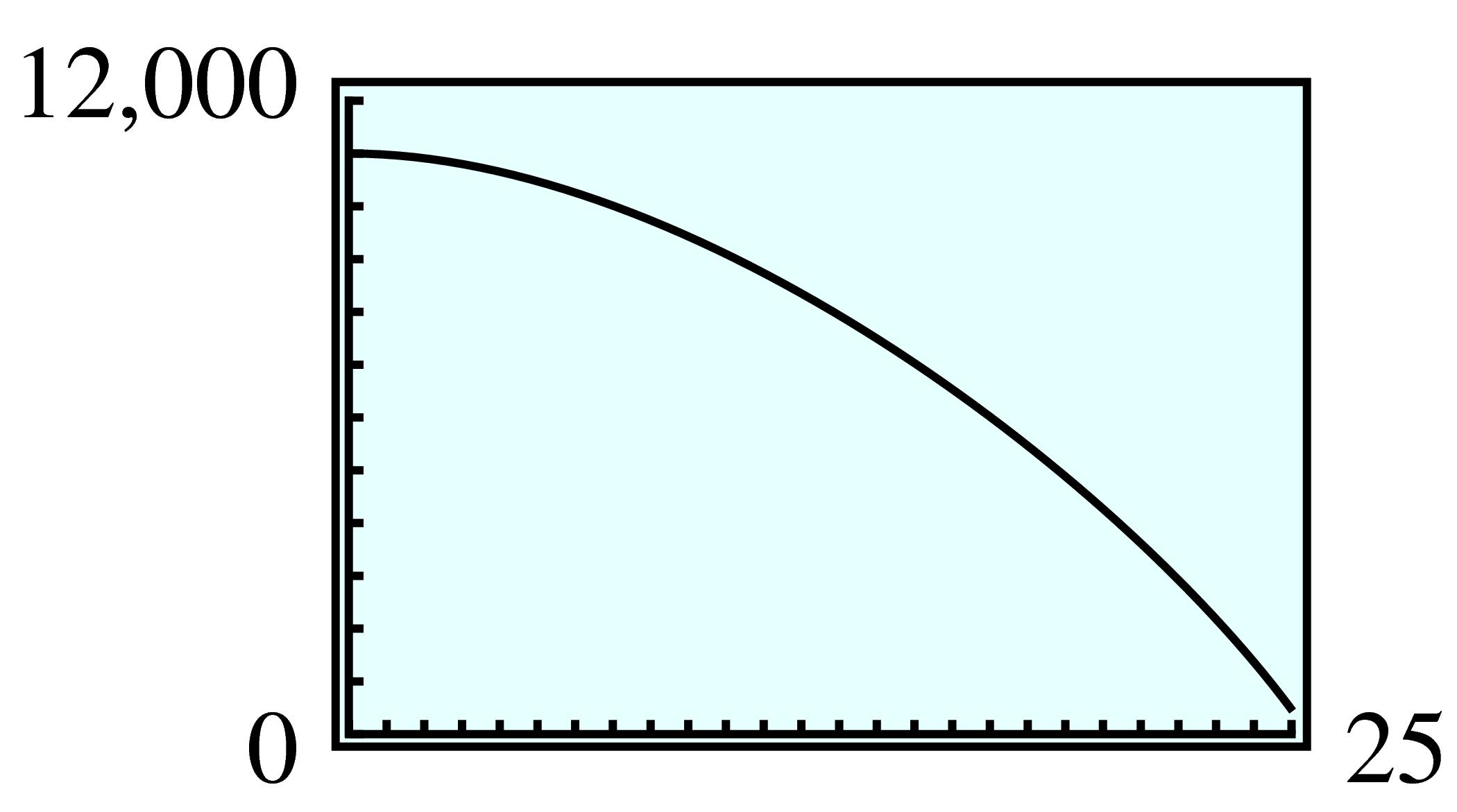
$t$ $0$ $5$ $10$ $15$ $20$ $25$

$h$ $11,000$ $10,520$ $9240$ $7160$ $4280$ $600$
$-16t^2 - 16t + 11,000 = 1000\text{;}$ $24.5$ sec
$1.2$ sec

41.

Answer.

$\displaystyle 2l + 4w = 100$
$\displaystyle l = 50 - 2w$
$w(50 - 2w) = 250\text{;}$ $~w = 6.91\text{,}$ $~18.09$
$12.06$ m by $6.91$ m, or $4.61$ m by $18.09$ m

43.

Answer.

$47.2$ mi
$1.26$ mi

45.

Answer.

$w= \dfrac{-4l\pm \sqrt{16l^2+8A}}{4} = \dfrac{-2l\pm \sqrt{4l^2+2A}}{2} $

47.

Answer.

$t = \dfrac{4 \pm \sqrt{16+64h}}{32} = \dfrac{1 \pm \sqrt{1+4h}}{8} $

49.

Answer.

$t=\dfrac{v \pm \sqrt{v^2-2as}}{a} $

51.

Answer.

$y=\dfrac{-x \pm \sqrt{8-11x^2}}{2} $

53.

Answer.

$0, ~x^2$

55.

Answer.

$\dfrac{-3x\pm 3}{2} $

57.

Answer.

$\dfrac{\pm \sqrt{4x^2-36}}{3}=\dfrac{\pm 2 \sqrt{x^2-9}}{3}$

59.

Answer.

$\dfrac{\pm 2x}{5} $

61.

Answer.

$3\pm\sqrt{\dfrac{V}{\pi h}} $

63.

Answer.

$\pm\sqrt{\dfrac{2(E-mgh)}{m}} $

65.

Answer.

$\pm\sqrt{\dfrac{V}{2w}-s^2} $

67.

Answer.

$\dfrac{-b}{a} $

69.

Answer.

$\dfrac{-b\pm \sqrt{b^2-4c}}{2} $

6.3 Graphing Parabolas
Homework 6.3

1.

Answer.

The parabola opens up, twice as steep as the standard parabola.
The parabola is the standard parabola shifted 2 units up.
The parabola is the standard parabola shifted 2 units left.
The parabola is the standard parabola shifted 2 units down.

3.

Answer.

Vertex $(0, -16)\text{;}$ $x$-intercepts $(\pm 4, 0)$
Vertex $(0, 16)\text{;}$ $x$-intercepts $(\pm 4, 0)$
Vertex $(8, 64)\text{;}$ $x$-intercepts $(0, 0)$ and $(16,0) $
Vertex $(8, -64)\text{;}$ $x$-intercepts $(0, 0)$ and $(16,0) $

5.

Answer.

Vertex $(1, -3)\text{;}$ $x$-intercepts $(0, 0)$ and $(-2,0) $
Vertex $(1, -3)\text{;}$ $x$-intercepts $(0, 0)$ and $(2,0) $
Vertex $(0,6)\text{;}$ no $x$-intercepts
Vertex $(0,-6)\text{;}$ $x$-intercepts $(\pm\sqrt{2}, 0)$

7.

Answer.

9.

Answer.

$(2000, 400)\text{;}$ The largest annual increase in biomass, $400$ tons, occurs when the biomass is $2000$ tons.
$4000 \lt x \le 5000\text{;}$ When there are too many fish, there will not be enough food to support all of them.

11.

Answer.

$x$ $~~1~~$ $~~2~~$ $~~3~~$ $~~4~~$ $~~5~~$

$y$ $1.6$ $1.2$ $0.8$ $0.4$ $0$

$A$ $1.6$ $2.4$ $2.4$ $1.6$ $0$
$A = x(2 - 0.4x)$ or $A = 2x - 0.4x^2$
The maximum number of young marmots, on average, is $2.5\text{;}$ the optimal number of female marmots is $2.5\text{.}$

13.

Answer.

Vertex: $(-6, -1.5)\text{;}$ Horizontal intercepts $(-12, 0)$ and $(0, 0)\text{.}$ The point $(0, 0)$ means that no distance is required to stop a plane that is not moving.
$594$ ft/sec

15.

Answer.

$\left(\dfrac{3}{2},\dfrac{17}{4} \right) \text{,}$ maximum
$\left(\dfrac{2}{3},\dfrac{1}{9} \right) \text{,}$ minimum
$(-4.5,18.5) \text{,}$ maximum

17.

Answer.

$x$-intercepts: $\left(\frac{-1}{2} , 0\right)$ and $(4, 0)\text{;}$ $y$-intercept: $(0, 4)\text{;}$ vertex: $\left(\frac{7}{4},\frac{81}{8} \right)$

19.

Answer.

$x$-intercepts: $(-2, 0)$ and $(1, 0)\text{;}$ $y$-intercept: $(0, -1.2)\text{;}$ vertex: $(-0.5, -1.35)$

21.

Answer.

No $x$-intercepts; $y$-intercept: $(0, 7)\text{;}$ vertex: $(-2, 3)$

23.

Answer.

$x$-intercepts: $\left(-1\pm\sqrt{2},0 \right) \text{;}$ $y$-intercept: $(0, -1)\text{;}$ vertex: $(-1, -2)$

25.

Answer.

$x$-intercepts: $\left(\dfrac{3\pm\sqrt{3}}{2},0 \right) \text{;}$ $y$-intercept: $(0, -3)\text{;}$ vertex: $\left(\dfrac{3}{2},\dfrac{3}{2} \right) $

27.

Answer.

$f(x) = x^2 - 6x + 5\text{:}$ $x$-intercepts $(1, 0)$ and $(5, 0)\text{;}$ $g(x) = x^2 - 6x + 9\text{:}$ $x$-intercept $(3, 0)\text{;}$ $h(x) = x^2 - 6x + 12\text{:}$ No $x$-intercept.
$16, 0, -12\text{:}$ $D = 16$ means that there are two rational $x$-intercepts, $D = 0$ means that there is exactly one $x$-intercept, $D=-12$ means that there is no $x$-intercept.

29.

Answer.

Two complex solutions

31.

Answer.

One repeated rational solution

33.

Answer.

Two distinct real solutions

35.

Answer.

37.

Answer.

Yes

39.

Answer.

$\displaystyle 2-\sqrt{5} $
$\displaystyle x^2-4x-1=0$

41.

Answer.

$\displaystyle 4+3\sqrt{2} $
$\displaystyle x^2-8x-2=0$

43.

Answer.

45.

Answer.

$y=x^2+x-6\text{;}$ $~x=\dfrac{-1}{2} $
$y=2x^2+2x-12\text{;}$ $~x=\dfrac{-1}{2} $

47.

Answer.

$\displaystyle (-1, -1), (-2, -4), (-3, -9), (-4, -16)$
$\displaystyle y=-x^2$
The vertex of $y = x^2 + 2kx$ is $(-k, -k^2)$

49.

Answer.

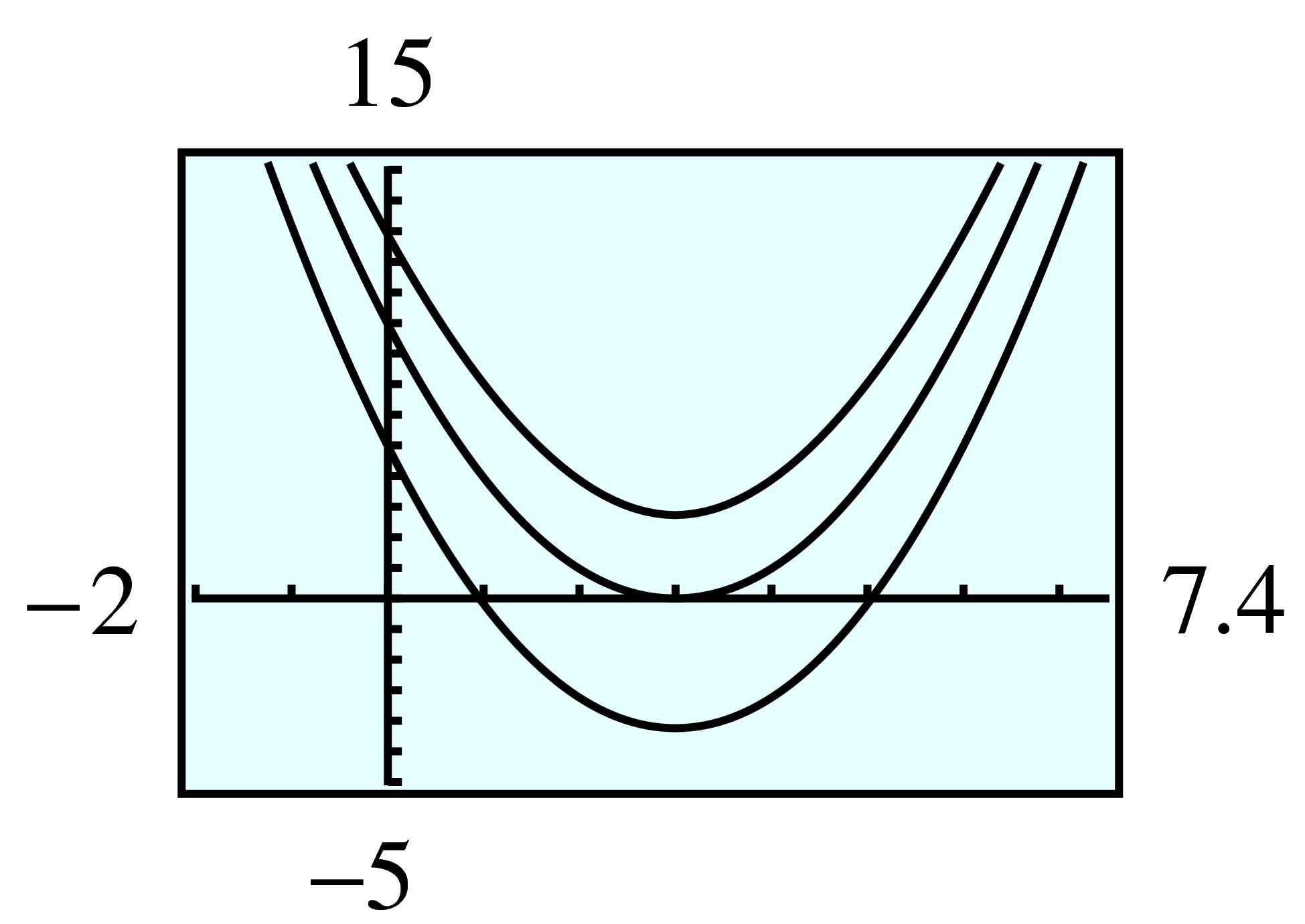
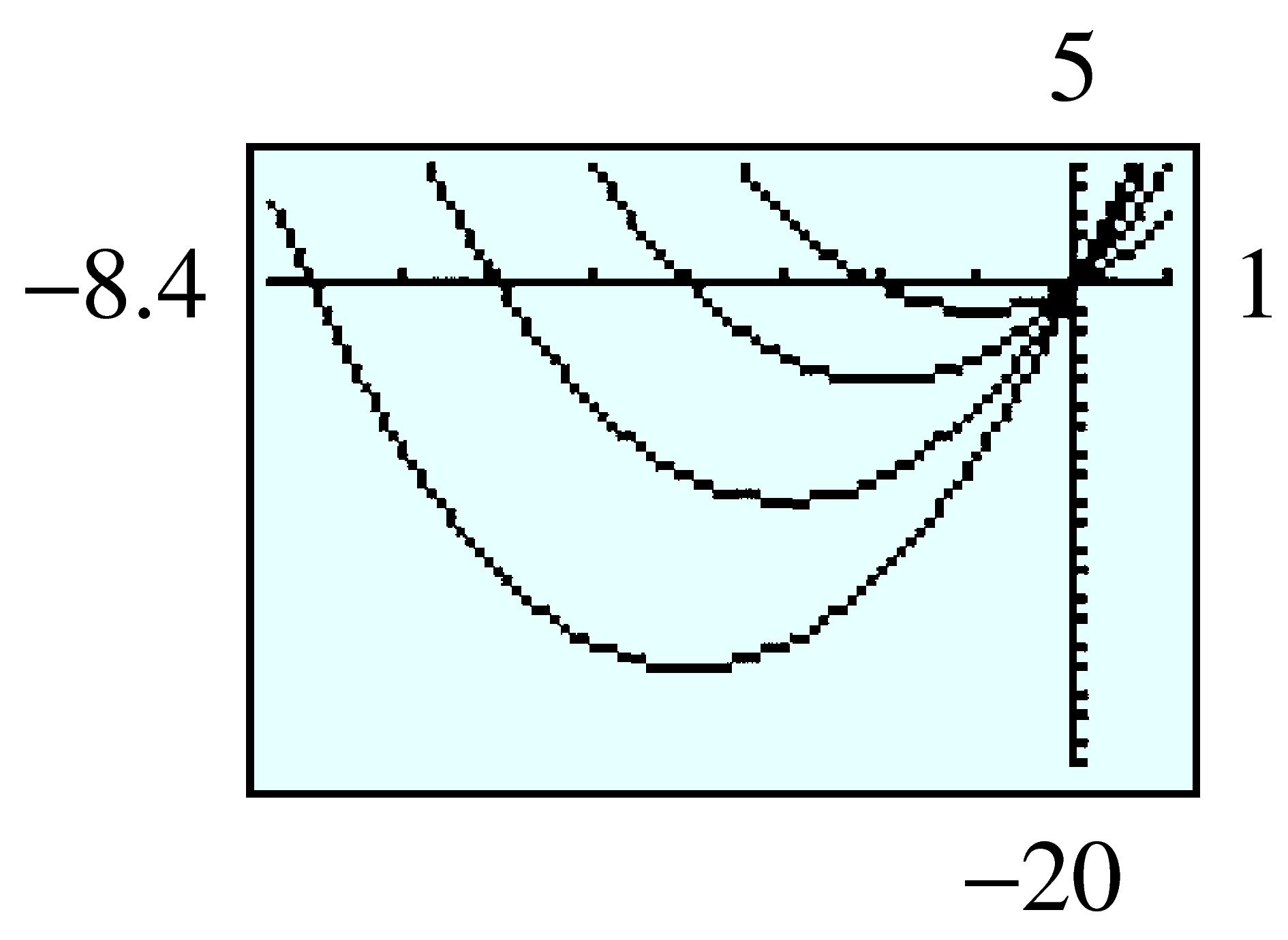
$t$	$0$	$0.5$	$1.0$	$1.5$	$2.0$	$2.5$	$3.0$	$3.5$
$x$	$0$	$6.075$	$11.5$	$16.275$	$20.4$	$23.875$	$26.7$	$28.875$
$y$	$0$	$7.44$	$12.48$	$15.12$	$15.36$	$13.2$	$8.64$	$1.68$

$y\approx 15.4$ m
$x\approx 30$ m
$3.6$ sec
$x\approx 29.2$ m
$y\approx 15.55$ m

6.4 Problem Solving
Homework 6.4

1.

Answer.

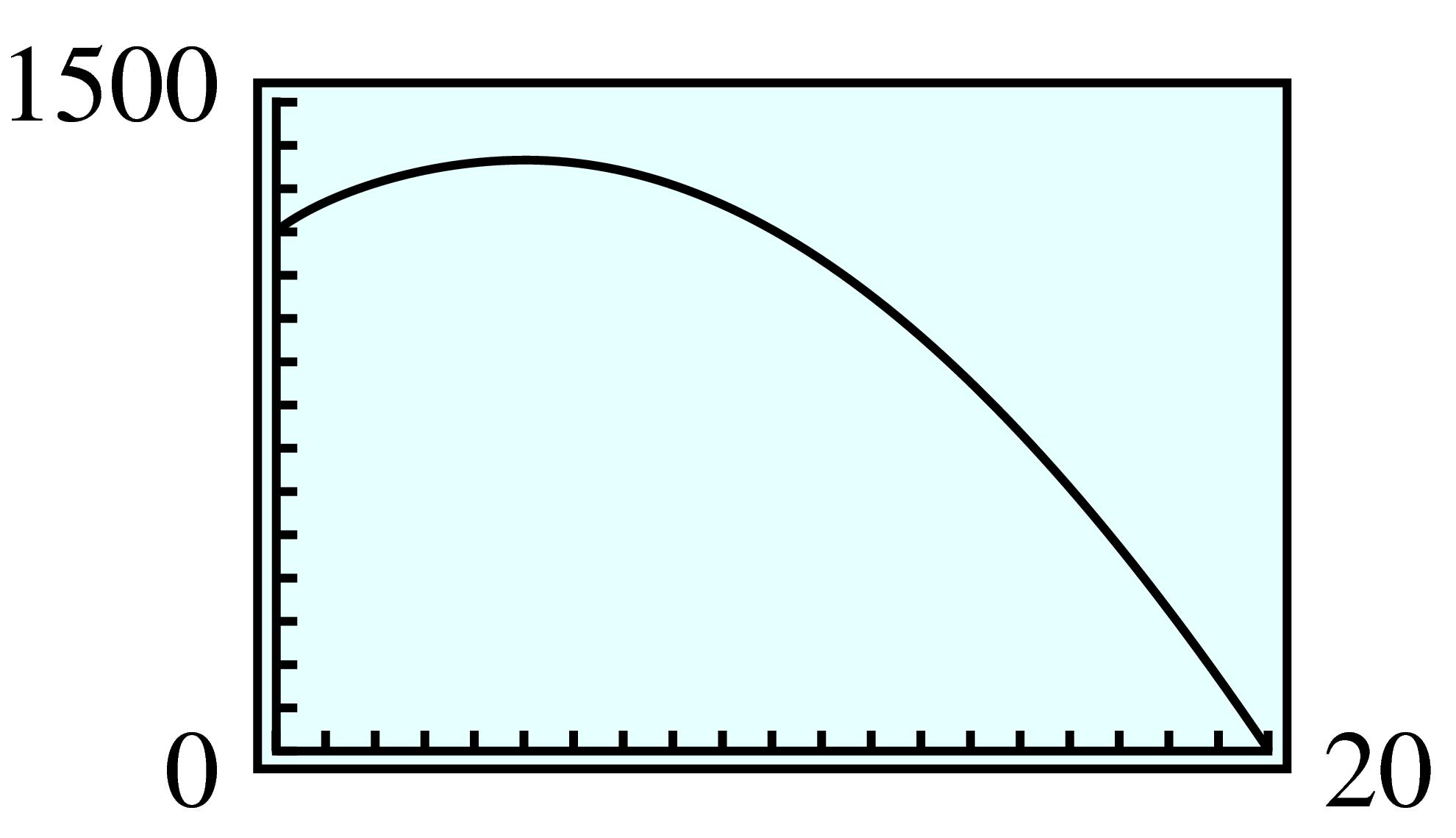
No. of price increases	Price of room	No. of rooms rented	Total revenue
$0$	$20$	$60$	$1200$
$1$	$22$	$57$	$1254$
$2$	$24$	$54$	$1296$
$3$	$26$	$51$	$1326$
$4$	$28$	$48$	$1344$
$5$	$30$	$45$	$1350$
$6$	$32$	$42$	$1344$
$7$	$34$	$39$	$1326$
$8$	$36$	$36$	$1296$
$10$	$40$	$30$	$1200$
$12$	$44$	$24$	$1056$
$16$	$52$	$12$	$624$
$20$	$60$	$0$	$0$

Price of a room: $20 + 2x\text{;}$ Rooms rented: $60 - 3x\text{;}$ Revenue: $1200 + 60x - 6x^2$
$\displaystyle 20$
$$24;~$ $$36$
$$1350;~$ $$30;$ $~45~$rooms

3.

Answer.

(For example) $10$ m by $20$ m with area $200$ sq m; or $15$ m by $15$ m, area $225$ sq m
$\displaystyle 30-x$
$\displaystyle 30x-x^2$

5.

Answer.

$3$ sec, $144$ ft

7.

Answer.

$100$ baskets, $\$2000$

9.

Answer.

Length: $50 - w\text{;}$ Area: $50w - w^2$
$625$ sq in

11.

Answer.

$\displaystyle 300w - 2w^2$
$11,250$ sq yd

13.

Answer.

Number of people: $16 + x\text{;}$ Price per person: $2400 - 100x\text{;}$ Total revenue: $38,400 + 800x - 100x^2$
$\displaystyle 20$

15.

Answer.

$a = 0.9\text{;}$ $I = \$865.80$

17.

Answer.

19.

Answer.

21.

Answer.

$\displaystyle (3,4)$
$\displaystyle y = 2x^2 - 12x + 22$

23.

Answer.

$\displaystyle (-4,-3)$
$\displaystyle y = \dfrac{-1}{2} x^2 - 4x -11$

25.

Answer.

$\displaystyle y = (x - 2)^2 + 3$

27.

Answer.

$\displaystyle y = 3(x + 1)^2 - 5$

29.

Answer.

$\displaystyle y=-2(x + 2)^2 + 11$

31.

Answer.

No solutions:

One solution:

Two solutions:

two parabolas intersecting in two points

33.

Answer.

$(-1, 12), (4, 7)$

35.

Answer.

$(-2, 7) $

37.

Answer.

No solution

39.

Answer.

$(-2, -5), (5, 16)$

41.

Answer.

$(1, 4)$

43.

Answer.

$(3,1)$

45.

Answer.

Larger, by $75$ tons. Smaller, by $125$ tons.
$1000$ tons and $3000$ tons
The fish population will decrease each year until it is completely depleted.

47.

Answer.

$K\gt N\text{.}$ The population will decrease by $48$ bears.
The population will increase by $18$ bears.
$\displaystyle 1000$
Populations between $0$ and $1000$ will increase; populations over $1000$ will decrease.
$1000$ (unless the population is $0$)
$500$ (unless the population is $0$)

49.

Answer.

$\displaystyle (200,~ 2600), (1400,~ 18,200)$
$\displaystyle x=800$

51.

Answer.

$\displaystyle (60,~ 39,000), (340,~ 221,000)$
$\displaystyle x=200$

53.

Answer.

See graph and (c)
$\displaystyle ad^2+k$
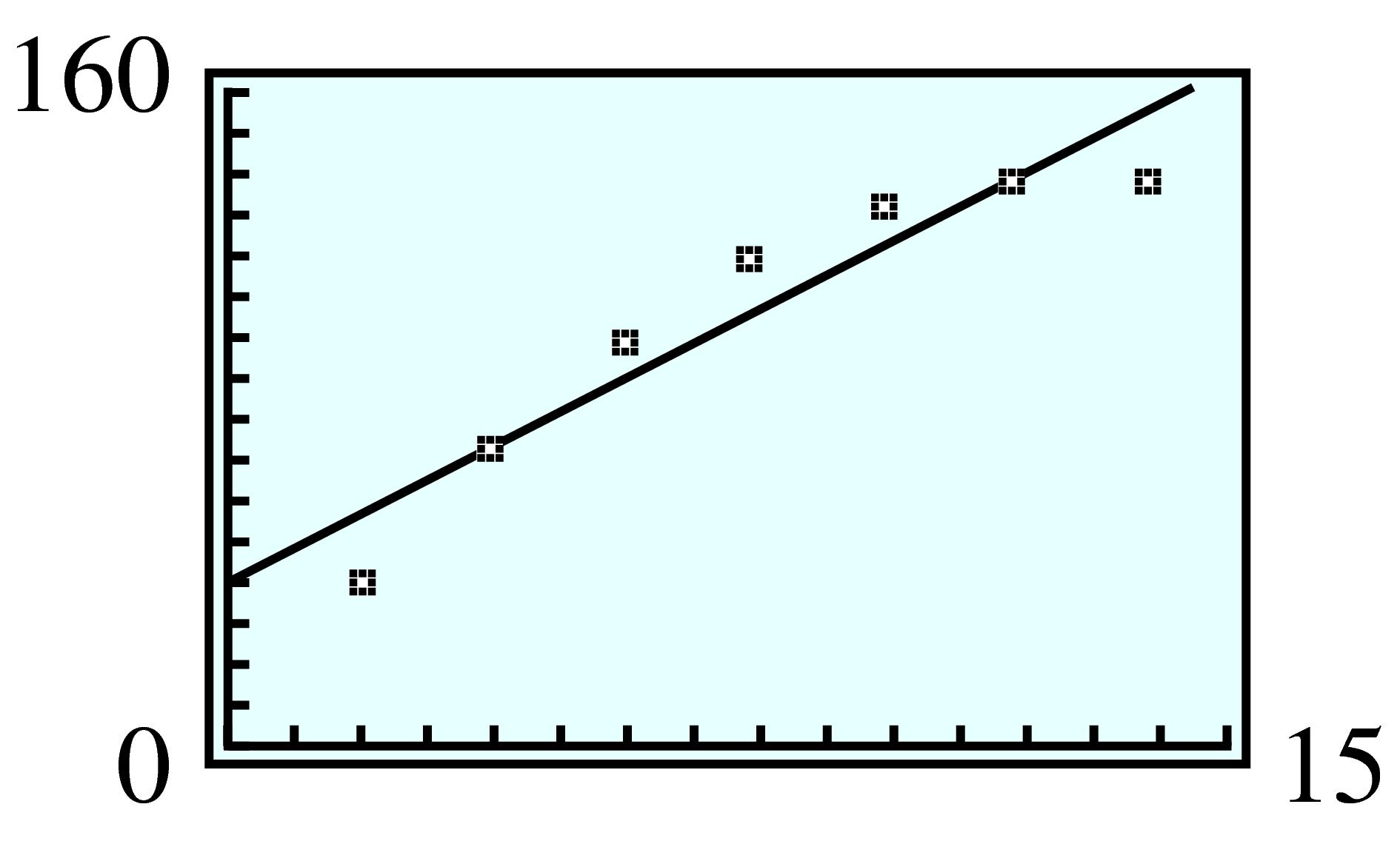
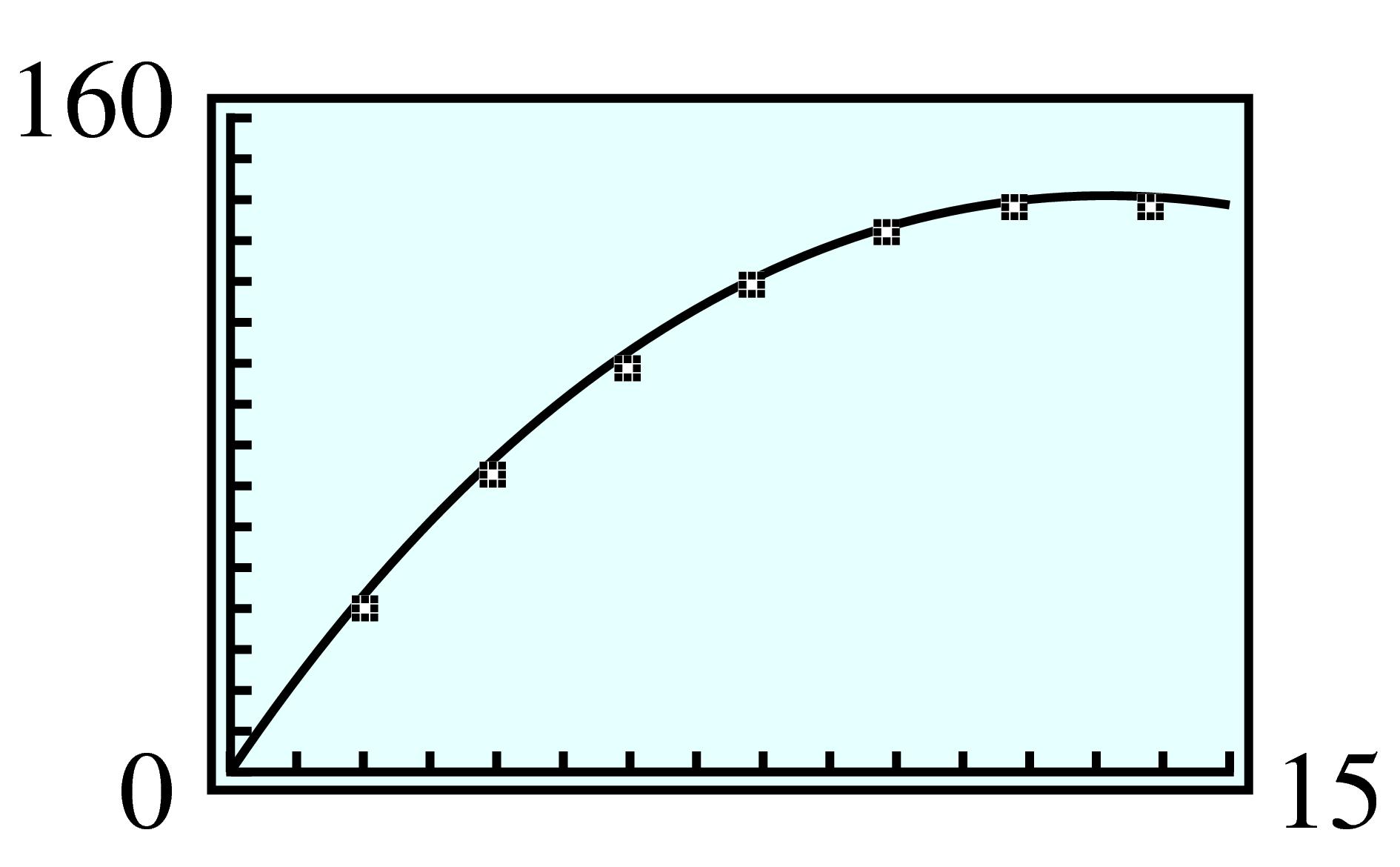
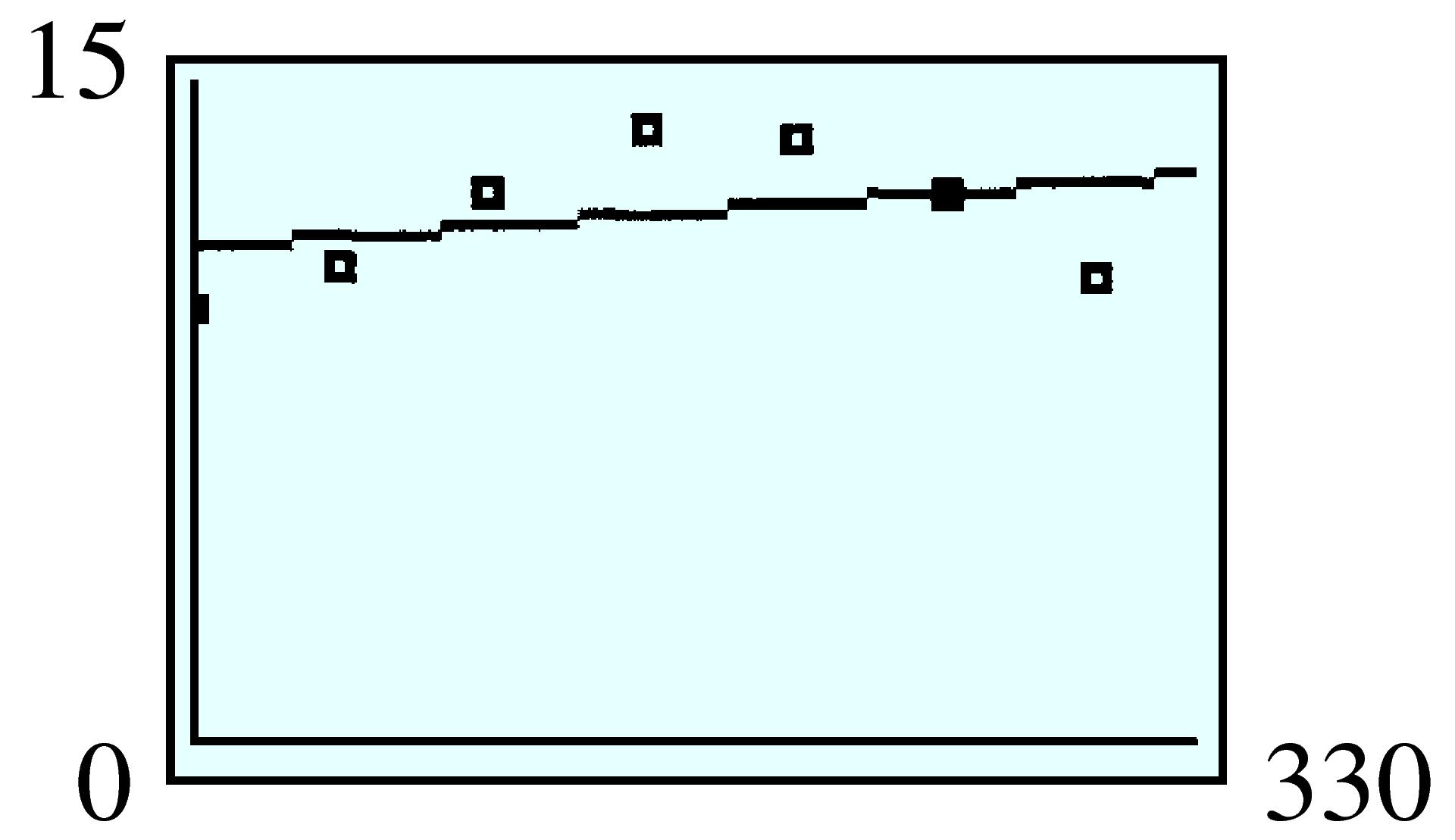
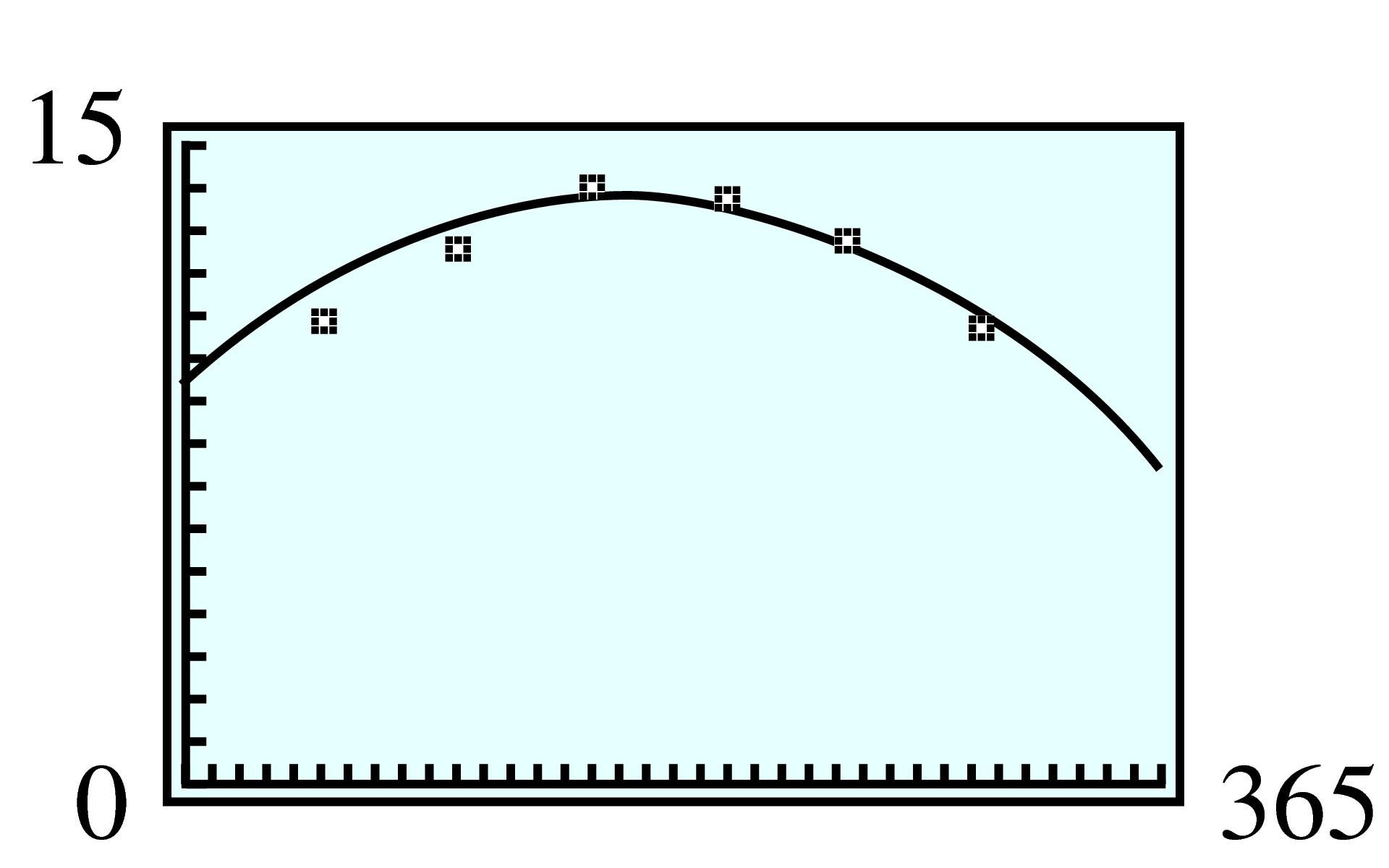
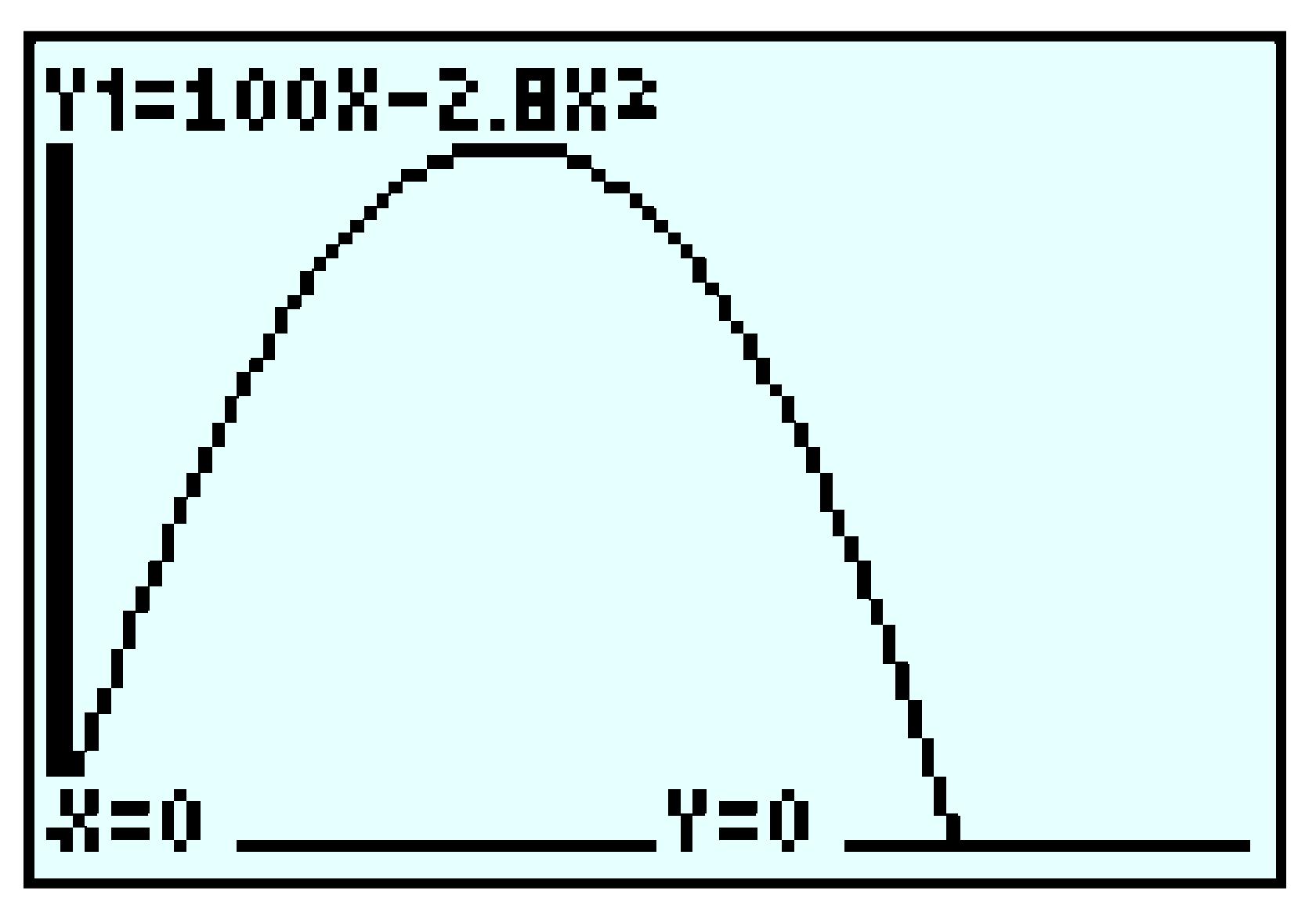
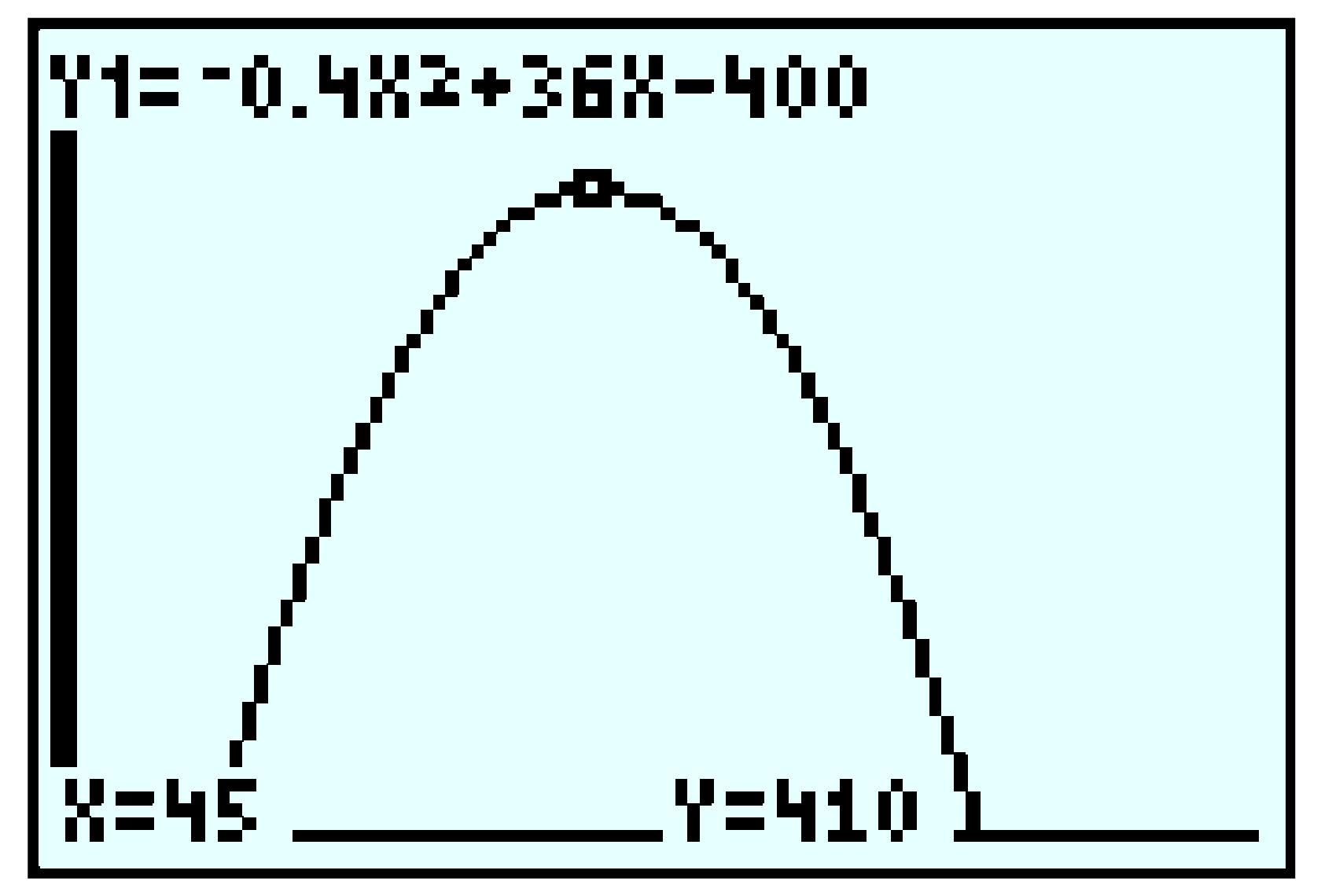
The two points on the parabola that are the same horizontal distance from the line $x = h$ the axis of symmetry have the same $y$-coordinate, so they are symmetric about that line.

6.5 Quadratic Inequalities
Homework 6.5

1.

Answer.

See graph
$x\gt 3$ or $x\lt -3\text{.}$ It omits the solutions $x \lt -3\text{.}$

3.

Answer.

See graph
$x\gt 3$ or $x\lt -1$

5.

Answer.

$\displaystyle -12, 15$
$x\lt -12$ or $x\gt 15$

7.

Answer.

$\displaystyle 0.3, 0.5$
$\displaystyle 0.3 \le x \le 0.5$

9.

Answer.

$\displaystyle (-\infty, -3) \cup (6, \infty)$
$\displaystyle (-3,6) $
$\displaystyle [-2,5] $
$\displaystyle (-\infty, -2] \cup [5, \infty)$

11.

Answer.

$\displaystyle (-4,4) $
$\displaystyle (-\infty, -4) \cup (4, \infty)$
$\displaystyle (-\infty, -3] \cup [3, \infty)$
$\displaystyle [-3,3] $

13.

Answer.

$(-\infty, -2) \cup (3, \infty)$

15.

Answer.

$[0, 4] $

17.

Answer.

$(\infty, -1)\cup (6, \infty) $

19.

Answer.

$(-4.8, 6.2)$

21.

Answer.

$(-\infty, -7.2] \cup [0.6, \infty) $

23.

Answer.

$(-\infty, 5.2) \cup (8.8, \infty) $

25.

Answer.

$x \lt - 3.5$ or $x \gt 3.5$

27.

Answer.

All $x$

29.

Answer.

$-10.6\lt x\lt 145.6$

31.

Answer.

$(-3, 4)$

33.

Answer.

$[-7, 4]$

35.

Answer.

$\left(-\infty, \dfrac{-1}{2}\right)\cup (4, \infty)$

37.

Answer.

$(-8, 8)$

39.

Answer.

$(-2.24, 2.24)$

41.

Answer.

$(-\infty, 0.4] \cup [6, \infty)$

43.

Answer.

$(-\infty, -0.67) \cup (0.5, \infty)$

45.

Answer.

$(-\infty, 0.27] \cup [3.73, \infty)$

47.

Answer.

All $m$

49.

Answer.

No solution

51.

Answer.

$320t - 16t^2 \gt 1024\text{;}$ $4 \lt t \lt 16\text{:}$ Between $4$ and $16$ seconds

53.

Answer.

$-0.02x^2 + 14x + 1600 \lt 2800\text{;}$ $[0, 100) \cup (600, 700]\text{:}$ Either less than $100$ or more than $600$ shears.

55.

Answer.

$p(1200 - 30p)\gt 9000\text{;}$ $10\lt p \lt 30\text{:}$ Between $$10$ and $$30$

57.

Answer.

$500\pi \lt 20\pi r^2 \lt 2880\pi\text{;}$ $5 \lt r \lt 12\text{;}$ The radius must be between $5$ and $12$ ft.

59.

Answer.

Size of group: $20 + x\text{;}$ Price per person: $600 - 10x$
$\displaystyle I = (20 + x)(600 - 10x)$
$$16,000\text{;}$ $~20$
Between 5 and 35

6.6 Curve Fitting
Homework 6.6

1.

Answer.

$a = -2, b = 3, c = -4$

3.

Answer.

$a = 1, b = -4, c = 7$

5.

Answer.

$a = 3, b = 1, c = -2\text{.}$ The equation for the parabola is $y = 3x^2 + x - 2$

7.

Answer.

$\displaystyle P = -0.16x^2 + 7.4x - 71$
$14\%\text{.}$ It predicts that $14\%$ of the $25$-year old population use marijuana on a regular basis.

9.

Answer.

$\displaystyle C = 0.75t^2 -1.85t + 56.2$
$65.7$ lb

11.

Answer.

$D=\dfrac{1}{2}n^2-\dfrac{3}{2}n $

13.

Answer.

$\displaystyle y= a(x + 2)^2 + 6$
$\displaystyle 3$

15.

Answer.

$\displaystyle y= \dfrac{3}{4}x^2-3 $
$y=ax^2-3 $ for any $a\lt 0$

17.

Answer.

$y = -2(x - 30)^2 + 280 $

19.

Answer.

$y=x^2 - 9$

21.

Answer.

$y=-2x^2 $

23.

Answer.

$y = x^2 - 2x - 15 $

25.

Answer.

$y = x^2 - 4x +5 $

27.

Answer.

$\displaystyle y=\dfrac{-1}{40}(x-80)^2+164 $
$160.99$ ft

29.

Answer.

Vertex: $\left( \frac{1991}{2} , 79\right)\text{;}$ $y$-intercept: $(0, 297)$
$\displaystyle y = 0.00022(x - 995.5)^2 + 79$

31.

Answer.

$8$ m
$\displaystyle y=\dfrac{x^2}{32} $
$3.125$ m

33.

Answer.

$\displaystyle h = 8.24t + 38.89$
$162.5$ m
$\displaystyle h=-0.81t^2 + 21.2t$
$135.7$ m
Quadratic: Gravity will slow the projectile, giving the graph a concave down shape.

35.

Answer.

$\displaystyle y=-0.587t^2 + 7.329t - 2.538$
The predicted peak was in 2000, near the end of March. The model predicts $7$ deaths for 2005.

37.

Answer.

$\displaystyle y = 0.0051t + 11.325$
$13.2$ hr
$\displaystyle y=-0.00016t^2 + 0.053t + 9.319$
$7.4$ hr
$9.8$ hr (the same as the previous year); Neither model is appropriate.

6.7 Chapter Summary and Review
Chapter 6 Review Problems

1.

Answer.

$0, ~\dfrac{-5}{2} $

3.

Answer.

$-1, ~2$

5.

Answer.

$-2, ~3$

7.

Answer.

$4x^2 - 29x - 24 = 0$

9.

Answer.

$y= (x - 3) (x + 2.4)$

11.

Answer.

$1\text{,}$ $~2$

13.

Answer.

$-1\text{,}$ $~\dfrac{1}{4} $

15.

Answer.

$2\pm \sqrt{10} $

17.

Answer.

$\dfrac{3\pm\sqrt{3} }{2} $

19.

Answer.

$1\text{,}$ $~2$

21.

Answer.

$2\pm \sqrt{2} $

23.

Answer.

$\pm\sqrt{\dfrac{2K}{m}} $

25.

Answer.

$\dfrac{3\pm\sqrt{9-3h} }{3} $

27.

Answer.

$9$

29.

Answer.

$10$ ft by $18$ ft or $12$ ft by $15$ ft

31.

Answer.

$1$ sec

33.

Answer.

$\displaystyle h = 100t - 2.8t^2$
$893$ ft
$15\frac{5}{7}$ sec on the way up and $20$ sec on the way down

35.

Answer.

$A_1$ is the area of a square minus the area of two triangles:

\begin{equation*} x^2-2\left(\dfrac{1}{2}y\cdot y \right)=x^2-y^2 \end{equation*}

37.

Answer.

Vertex and intercepts are all $(0,0) \text{.}$

39.

Answer.

Vertex $(\dfrac{9}{2},\dfrac{-81}{4})\text{;}$ $x$-intercepts $(9,0)$ and $(0,0)\text{;}$ $y$-intercept $(0,0) $

41.

Answer.

Vertex $(\dfrac{-1}{2},\dfrac{-25}{4})\text{;}$ $x$-intercepts $(-3,0)$ and $(2,0)\text{;}$ $y$-intercept $(0,-6) $

43.

Answer.

Vertex $(\dfrac{-1}{4},\dfrac{65}{8})\text{;}$ $x$-intercepts $\left(\dfrac{-1 \pm \sqrt{65}}{4} ,0 \right)\text{;}$ $y$-intercept $(0,8) $

45.

Answer.

Vertex $(\dfrac{1}{2},\dfrac{-37}{4})\text{;}$ $x$-intercepts $\left(\dfrac{1 \pm \sqrt{37}}{2} ,0 \right)\text{;}$ $y$-intercept $(0,-9) $

47.

Answer.

Two

49.

Answer.

One rational solution

51.

Answer.

No real solutions

53.

Answer.

$45\text{;}$ $$410$

55.

Answer.

$\displaystyle y = 60 (4 + x) (32 - 4x)$
$\displaystyle 2$

57.

Answer.

$\displaystyle 0, ~\dfrac{-3}{2} $
$\displaystyle \dfrac{5}{6} $
$\displaystyle -5, ~\dfrac{1}{2} $

59.

Answer.

$\displaystyle 0, ~1 $
None
$\displaystyle -1, ~3 $

61.

Answer.

$(-\infty ,-2) \cup (3,\infty )$

63.

Answer.

$\left[-1,\dfrac{3}{2} \right] $

65.

Answer.

$[-2,2] $

67.

Answer.

$\displaystyle R=p \left(220-\dfrac{1}{4}p \right) $
Between $$4.00$ and $$4.80$

69.

Answer.

$(1, 3)\text{,}$ $~(-1, 3)$

71.

Answer.

$(-1, -4)\text{,}$ $~(5, 20)$

73.

Answer.

$(-9, 155)\text{,}$ $~(5, 15)$

75.

Answer.

$(-1, 2)\text{,}$ $~(3, 0)$

77.

Answer.

$a=1\text{,}$ $~b=-1\text{,}$ $~c=-6$

79.

Answer.

$p(x)=\dfrac{-1}{2}x^2-4x+10 $

81.

Answer.

$y = 0.2 (x - 15)^2 -6$

83.

Answer.

$\displaystyle f (x) = (x - 12)^2 -100$

85.

Answer.

$\displaystyle y =\dfrac{1}{3} (x +3)^2 -2$

87.

Answer.

$\displaystyle h = 36.98t + 5.17$
$116.1$ m, $~153.1$ m
$\displaystyle h= -4.858t^2 + 47.67t + 0.89$
$100.2$ m, $~113.9$ m
Quadratic: Gravity will slow the cannonball, giving the graph a concave down shape.

7 Polynomial and Rational Functions
7.1 Polynomial Functions
Homework 7.1

1.

Answer.

$12x^3 - 5x^2 - 8x + 4$

3.

Answer.

$x^3 - 6x^2 + 11x - 6$

5.

Answer.

$6a^4 - 5a^3 - 5a^2 + 5a - 1$

7.

Answer.

$y^4 + 5y^3 - 20y - 16$

9.

Answer.

$6 + x + 5x^2$

11.

Answer.

$4 - 7x^2 - 8x^4$

13.

Answer.

$0x^2$

15.

Answer.

$-8x^3$

17.

Answer.

$\displaystyle 4$
$\displaystyle 5$
$\displaystyle 7$

19.

Answer.

$\begin{aligned}[t] (x + y)^3 \amp = (x + y)(x + y)^2\\ \amp = (x + y)(x^2 + 2xy + y^2) \\ \amp = x^3 + 2x^2 y + xy^2 + x^2 y + 2xy^2 + y^3\\ \amp = x^3 + 3x^2 y + 3xy^2 + y^3 \end{aligned}$

21.

Answer.

$\begin{aligned}[t] (x + y)(x^2 - xy + y^2) \amp = x^3 -x^2 y + xy^2 + x^2 y -xy^2 + y^3\\ \amp = x^3 + y^3 \end{aligned}$

23.

Answer.

The formula begins with $x^3$ and ends with $y^3\text{.}$ As you proceed from term to term, the exponents on $x$ decrease while the exponents on $y$ increase, and on each term the sum of the exponents is $3\text{.}$ The coefficients of the two middle terms are both $3\text{.}$
The formula is the same as for $(x - y)^3\text{,}$ except that the terms alternate in sign.

25.

Answer.

$1+6z+12z^2+8z^3$

27.

Answer.

$1-15\sqrt{t}+75t-125t\sqrt{t} $

29.

Answer.

$x^3-1$

31.

Answer.

$8x^3+1$

33.

Answer.

$27a^3 - 8b^3$

35.

Answer.

$(x+3)(x^2-3x+9) $

37.

Answer.

$(a-2b)(a^2+2ab+4b^2) $

39.

Answer.

$(xy^2-1)(x^2y^4+xy^2+1) $

41.

Answer.

$(3a+4b)(9a^2 -12ab+16b^2) $

43.

Answer.

$(5ab-1)(25a^2b^2+5ab+1) $

45.

Answer.

$(4t^3+w^2)(16t^6 -4t^3w^2+w^4) $

47.

Answer.

$\displaystyle \left(6-\dfrac{5}{4}\pi \right)x^2 $
$\approx 132.67$ square inches

49.

Answer.

$\displaystyle \dfrac{2}{3}\pi r^3+\pi r^2h $
$\displaystyle V(r)=\dfrac{14}{3}\pi r^3 $

51.

Answer.

$500(1 + r )^2\text{;}$ $500(1 + r )^3\text{;}$ $500(1 + r )^4 $
$500r^2 + 1000r + 500\text{;}$ $500r^3 + 1500r^2 + 1500r + 500\text{;}$ $500r^4 + 2000r^3 + 3000r^2 + 2000r + 500 $
$583.20, $629.86, $680.24

53.

Answer.

Length: $16 - 2x\text{;}$ Width: $12 - 2x\text{;}$ Height: $x$
$\displaystyle V = x(16 - 2x)(12 - 2x)$
Real numbers between $0$ and $6$
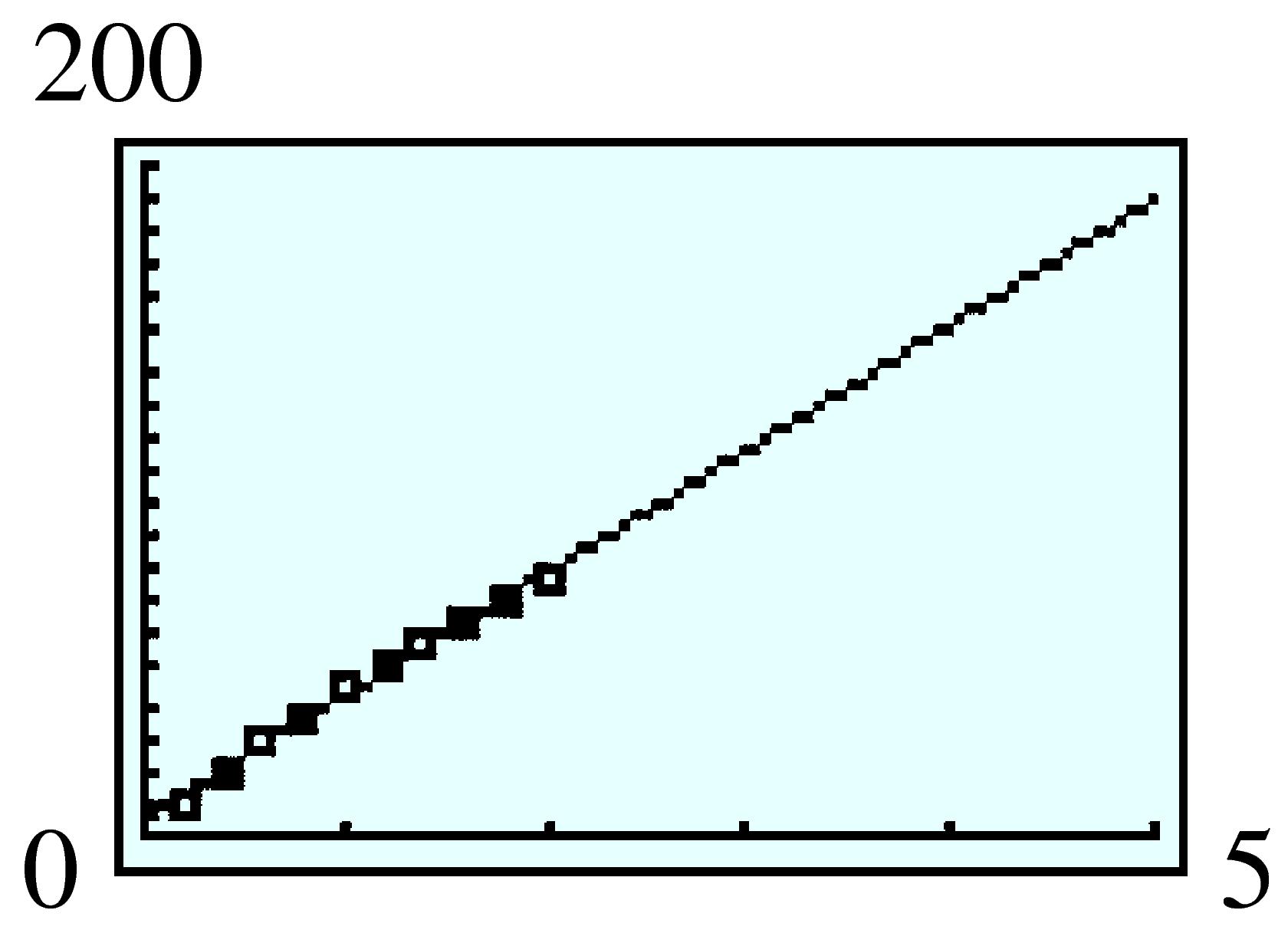
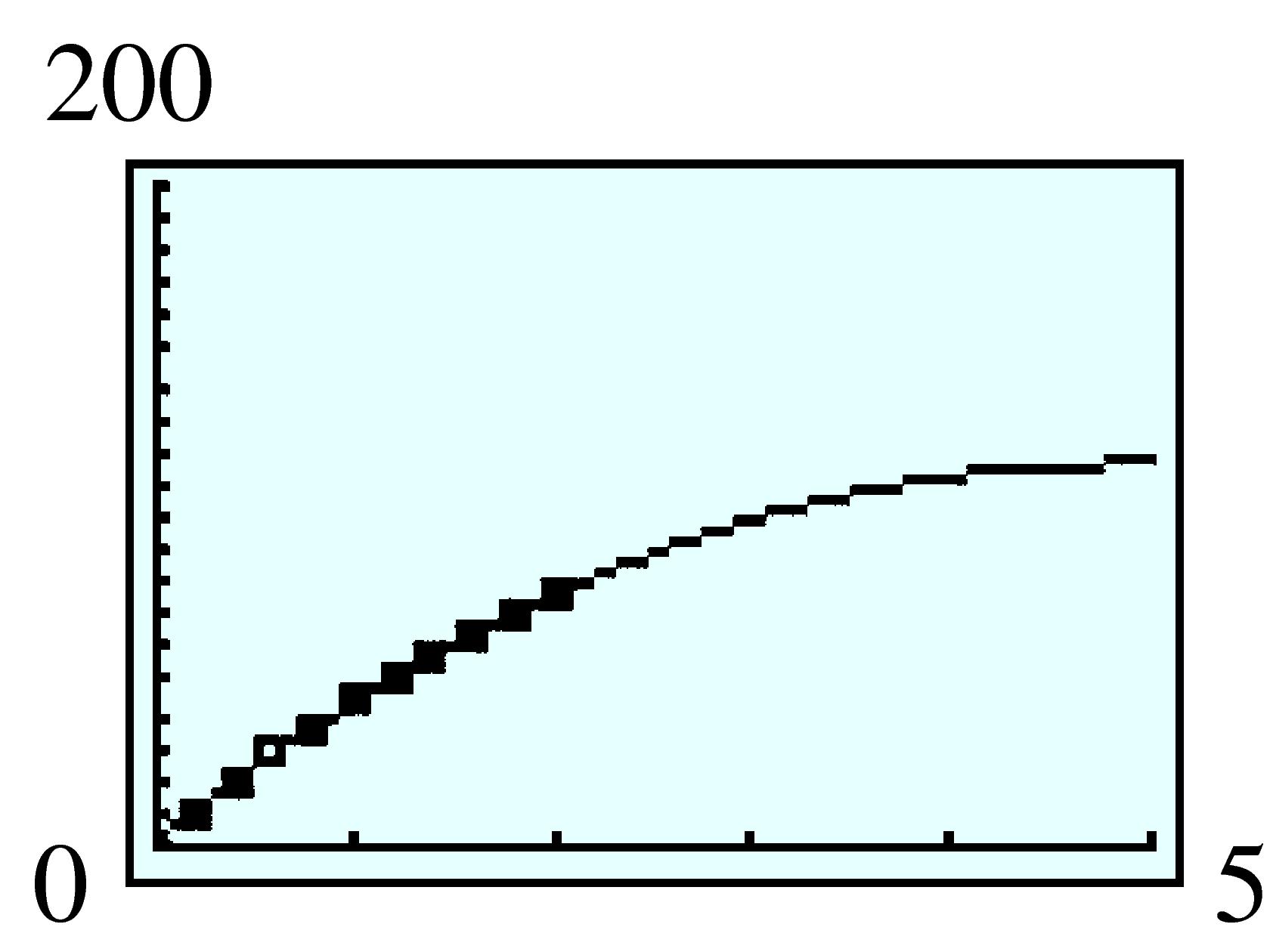
$x$ $1$ $2$ $3$ $4$ $5$

$V$ $140$ $192$ $180$ $128$ $60$
$2.26$ in, $194.07$ cu in

55.

Answer.

$\displaystyle 0, 9$
$0\le x \le 9\text{;}$ $R\ge 0$ for these values
$\dfrac{28}{3} $ points
$36$ points
$3$ ml or $8.2$ ml

57.

Answer.

$900\text{;}$ $11,145\text{;}$ $15,078$
$1341\text{;}$ $171\text{;}$ $627$
Between 1990 and 1991

59.

Answer.

The graph is concave down until about $x = 12.5$ and is concave up afterwards. The cost is growing at the slowest rate at the inflection point at about $x = 12.5\text{,}$ or $1250$ students.
About $2890$

61.

Answer.

$20$ cm
$100$ cm

63.

Answer.

$\displaystyle 763.10 \lt H(t) \lt 864$
$864$ min
$859.8$ min
Within $34$ days of the summer solstice
More than $66$ days from the summer solstice

7.2 Graphing Polynomial Functions
Homework 7.2

1.

Answer.

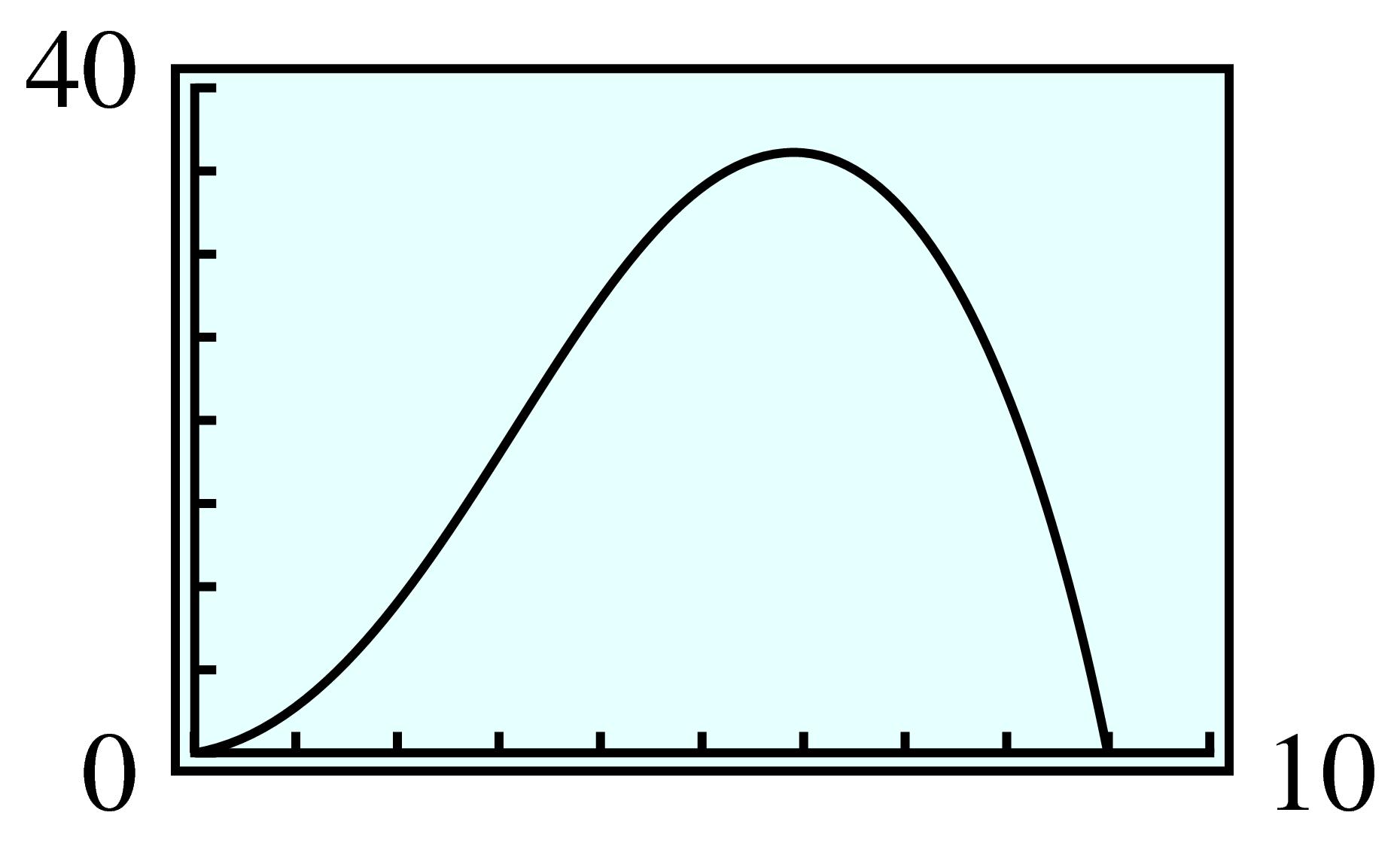
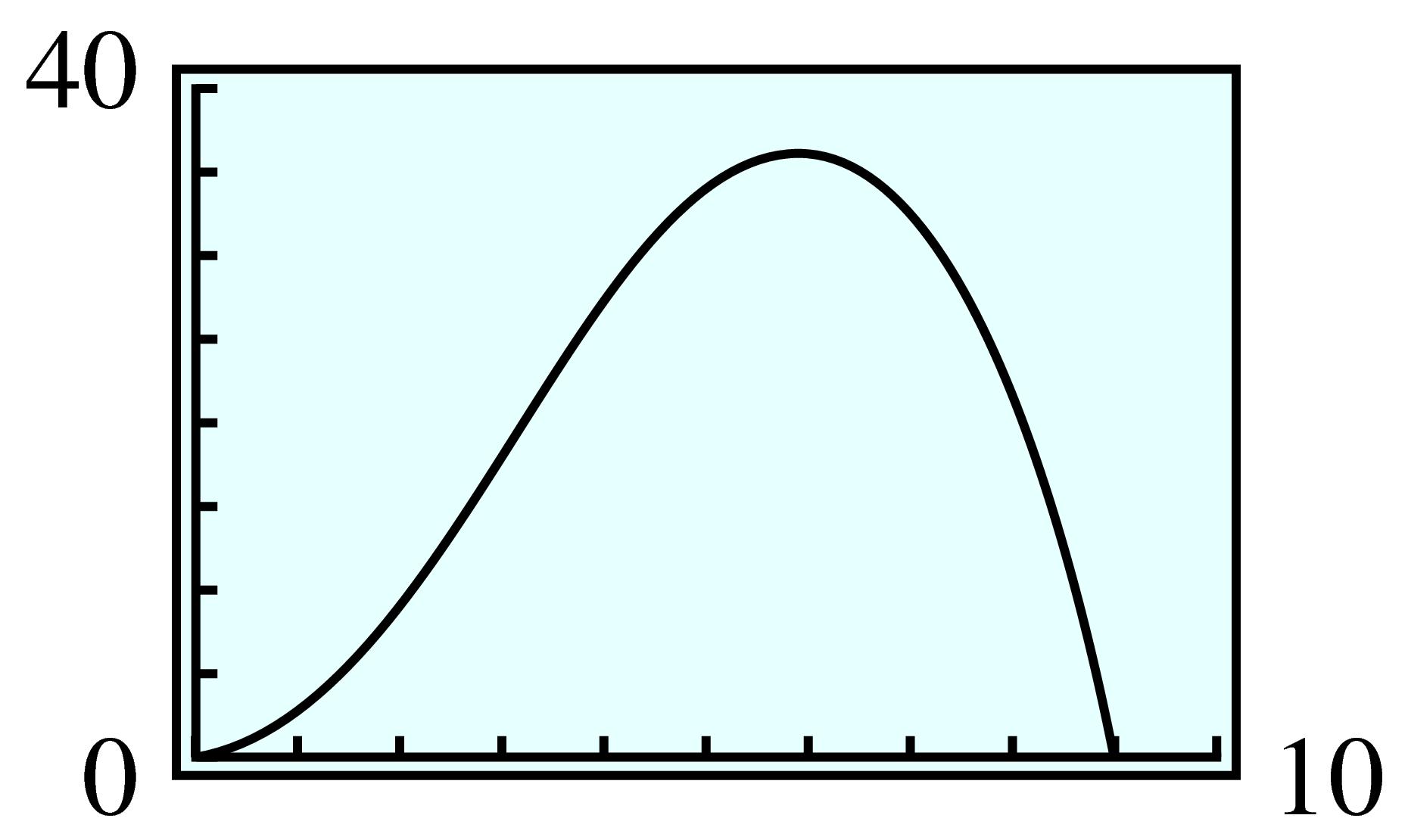
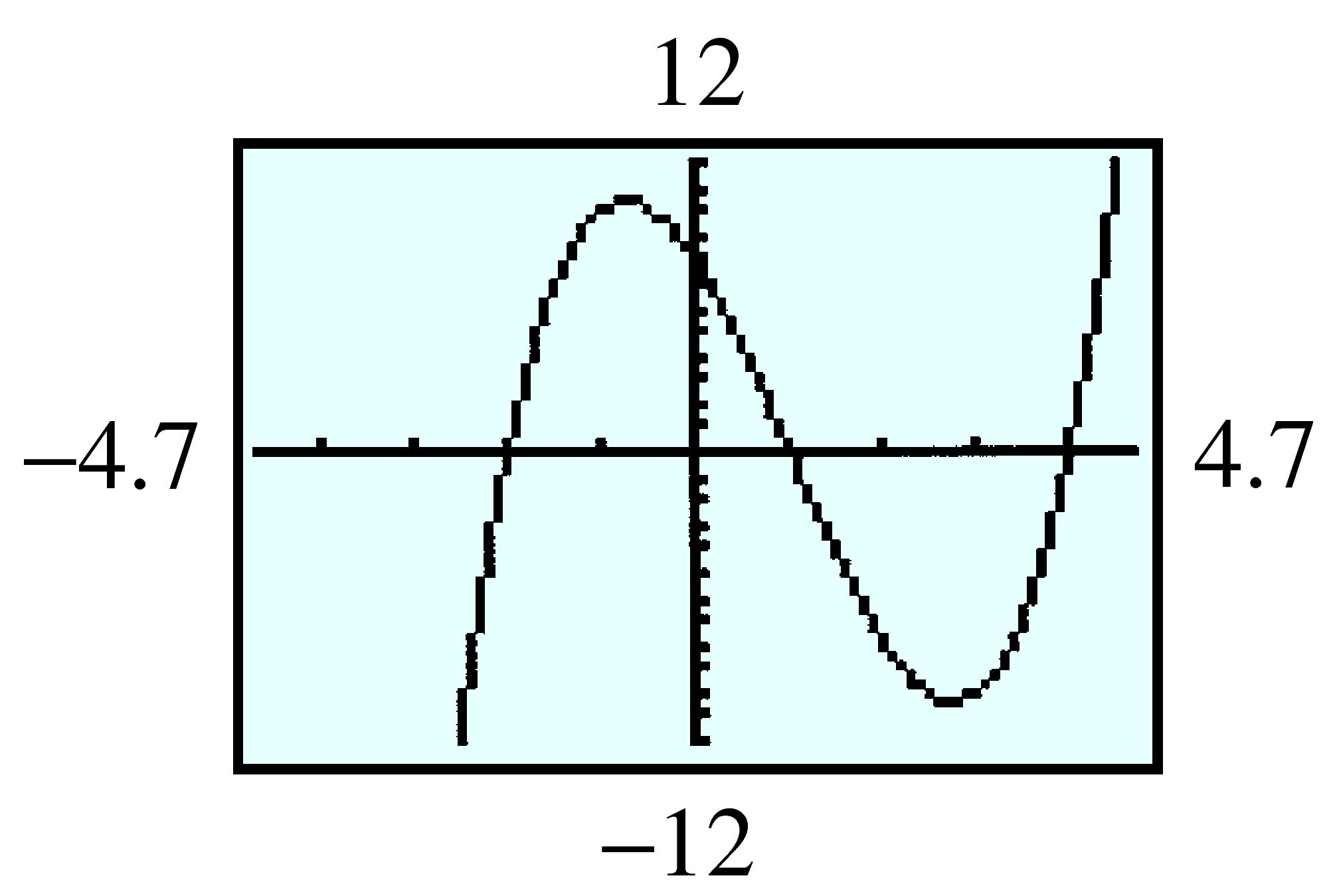
The end behavior is the same as for the basic cubic because the lead coefficient is positive.
There is one $x$-intercept, no turning points, one inflection point.

3.

Answer.

The end behavior is the opposite to the basic cubic (the graph starts in the upper left and extends to the lower right) because the lead coefficient is negative.
There is one $x$-intercept, no turning points, one inflection point.

5.

Answer.

The end behavior is the same as for the basic cubic because the lead coefficient is positive.
There are three $x$-intercepts, two turning points, one inflection point.

7.

Answer.

The end behavior is the same as for the basic cubic because the lead coefficient is positive.
There are three $x$-intercepts, two turning points, one inflection point.

9.

Answer.

(b) and (c) are the same.

11.

Answer.

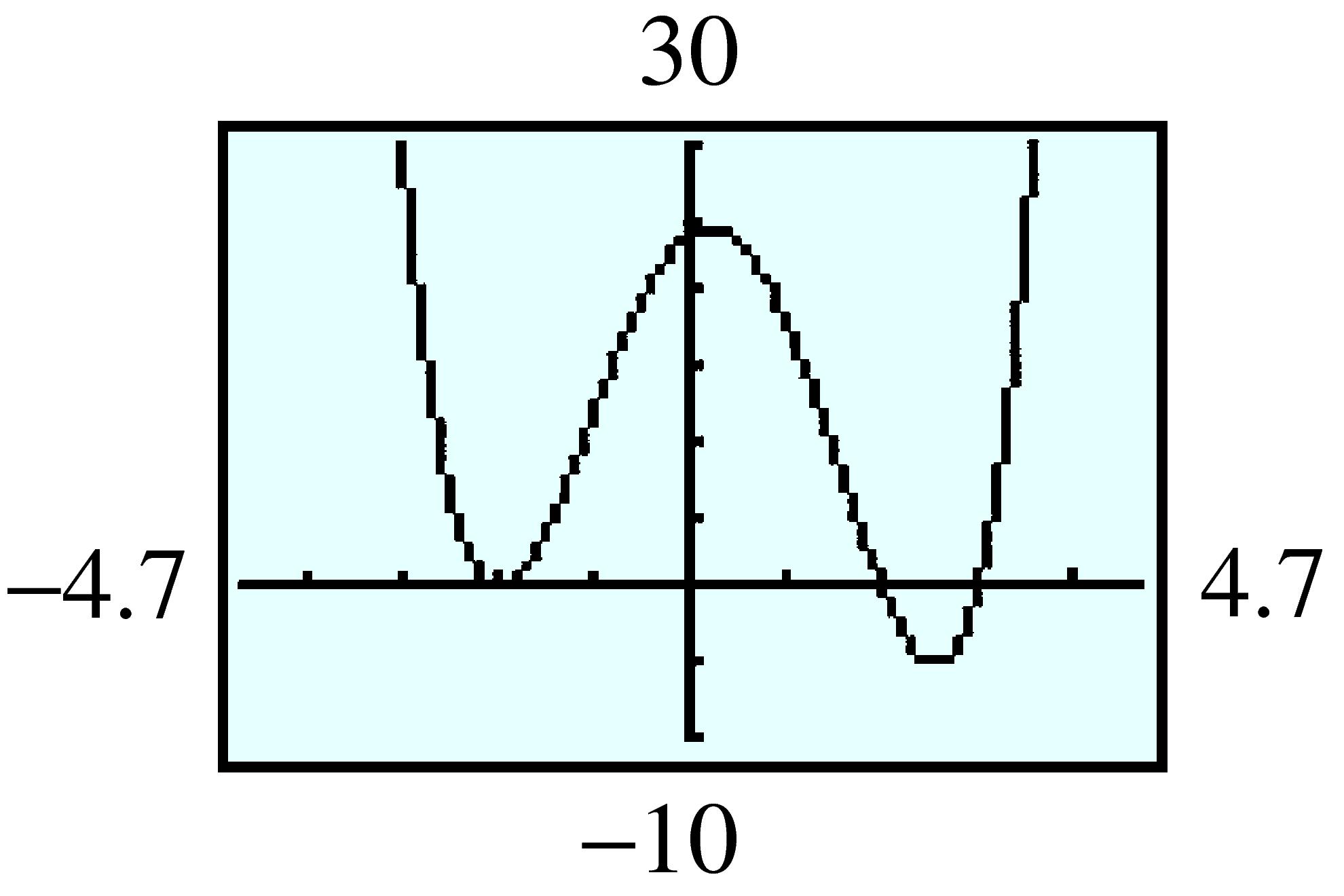
The end behavior is the same as for the basic quartic because the lead coefficient is positive.
There are two $x$-intercepts, one turning point, no inflection point.

13.

Answer.

The end behavior is the opposite of the basic quartic (the graph starts in the lower left and ends in the lower right) because the lead coefficient is negative.
There are no $x$-intercepts, three turning points, two inflection points.

15.

Answer.

The end behavior is the same as for the basic quartic because the lead coefficient is positive.
There are two $x$-intercepts, one turning point, two inflection points.

17.

Answer.

The end behavior is the opposite of the basic quartic (the graph starts in the lower left and ends in the lower right) because the lead coefficient is negative.
There are no $x$-intercepts, one turning point, two inflection points.

19.

Answer.

The graph of a cubic polynomial with a positive lead coefficient will have the same end behavior as the basic cubic, and a cubic with a negative lead coefficient will have the opposite end behavior. Each graph of a cubic polynomial has one, two, or three $x$-intercepts, it has two, one or no turning point, and it has exactly one inflection point.

21.

Answer.

$\displaystyle (-2, 0), (-1, 0), (3, 0)$
$\displaystyle P(x) = (x + 2)(x + 1)(x - 3)$
Yes

23.

Answer.

$\displaystyle (-2, 0), (0, 0), (1, 0), (2, 0)$
$\displaystyle R(x) = (x + 2)(x)(x - 1)(x - 2)$
Yes

25.

Answer.

$\displaystyle (-2, 0), (1, 0), (4, 0)$
$\displaystyle p(x) = (x + 2)(x - 1)(x - 4)$
Yes

27.

Answer.

$\displaystyle (-2, 0), (2, 0), (3, 0)$
$\displaystyle r(x) = (x + 2)^2(x - 2)(x - 3)$
Yes

29.

Answer.

31.

Answer.

33.

Answer.

35.

Answer.

37.

Answer.

$0$ (multiplicity 2)

39.

Answer.

$0$ (multiplicity 2), $2$ (multiplicity 2)

41.

Answer.

$\displaystyle 0, \pm 2$

43.

Answer.

$\displaystyle \pm\sqrt{2}, \pm\sqrt{8}$

45.

Answer.

$\pm 1, -3$ (multiplicity 2)

47.

Answer.

$P(x) = (x + 2)(x - 1)(x - 4)$

49.

Answer.

$P(x) = (x + 3)^2(x - 2)$

51.

Answer.

$P(x) = (x - 2)^3(x + 2)$

53.

Answer.

$y = x^3 - 4x + 3\text{;}$ The graph of $y = f (x)$ shifted $3$ units up.
$y = x^3 - 4x -5\text{;}$ The graph of $y = f (x)$ shifted $5$ units down.
$y = (x - 2)^3 - 4(x - 2)\text{;}$ The graph of $y = f (x)$ shifted $2$ units right.
$y = (x +3)^3 - 4(x +3)\text{;}$ The graph of $y = f (x)$ shifted $3$ units left.

55.

Answer.

$y = x^4 - 4x^2 + 6\text{;}$ The graph of $y = f (x)$ shifted $6$ units up.
$y = x^4 - 4x^2 - 2\text{;}$ The graph of $y = f (x)$ shifted $2$ units down.
$y = (x - 1)^4 - 4(x - 1)^2\text{;}$ The graph of $y = f (x)$ shifted $1$ unit right.
$y = (x +2)^4 - 4(x +2)^2\text{;}$ The graph of $y = f (x)$ shifted $2$ units left.

57.

Answer.

$q(x) = 2x^2 + 4x - 7\text{;}$ $r (x) = -32$

59.

Answer.

$q(x) = x^3 - 6x\text{;}$ $r (x) =-6x + 5$

61.

Answer.

If $P(x)$ is a nonconstant polynomial with real coefficients and $a$ is any real number, then there exist unique polynomials $q(x)$ and $r (x)$ such that

\begin{equation*} P(x) = (x - a)q(x) + r (x) \end{equation*}

where $\text{deg }r (x)\lt \text{deg }(x - a)\text{.}$
Zero
$P(a) = (a - a)q(a) + r (a) = r (a)\text{.}$ Because $\text{deg }r(x) = 0 \text{,}$ $r(x) $ is a constant. That constant value is $P(a) \text{,}$ so $P(x) = (x - a)q(x) + P(a)\text{.}$

63.

Answer.

From the remainder theorem, $\begin{aligned}[t] P(x) \amp = (x - a)Q(x) + P(a)\\ \amp = (x - a)Q(x) + 0\\ \amp =(x - a)Q(x) \end{aligned}$
By definition of a factor, if $x-a$ is a factor of $P(x) \text{,}$ then $P(x) = (x - a)q(x)\text{,}$ so $P(x) =(x - a)q(x) + 0\text{.}$ The uniqueness guaranteed in the remainder theorem tells us that $P(a) = 0\text{.}$

65.

Answer.

$\displaystyle P(1)=0 $
$\displaystyle \dfrac{1\pm\sqrt{5}}{2} $

67.

Answer.

$\displaystyle P(-3)=0 $
$\displaystyle 0, 2, 4 $

69.

Answer.

About $-1\lt x \lt 2$

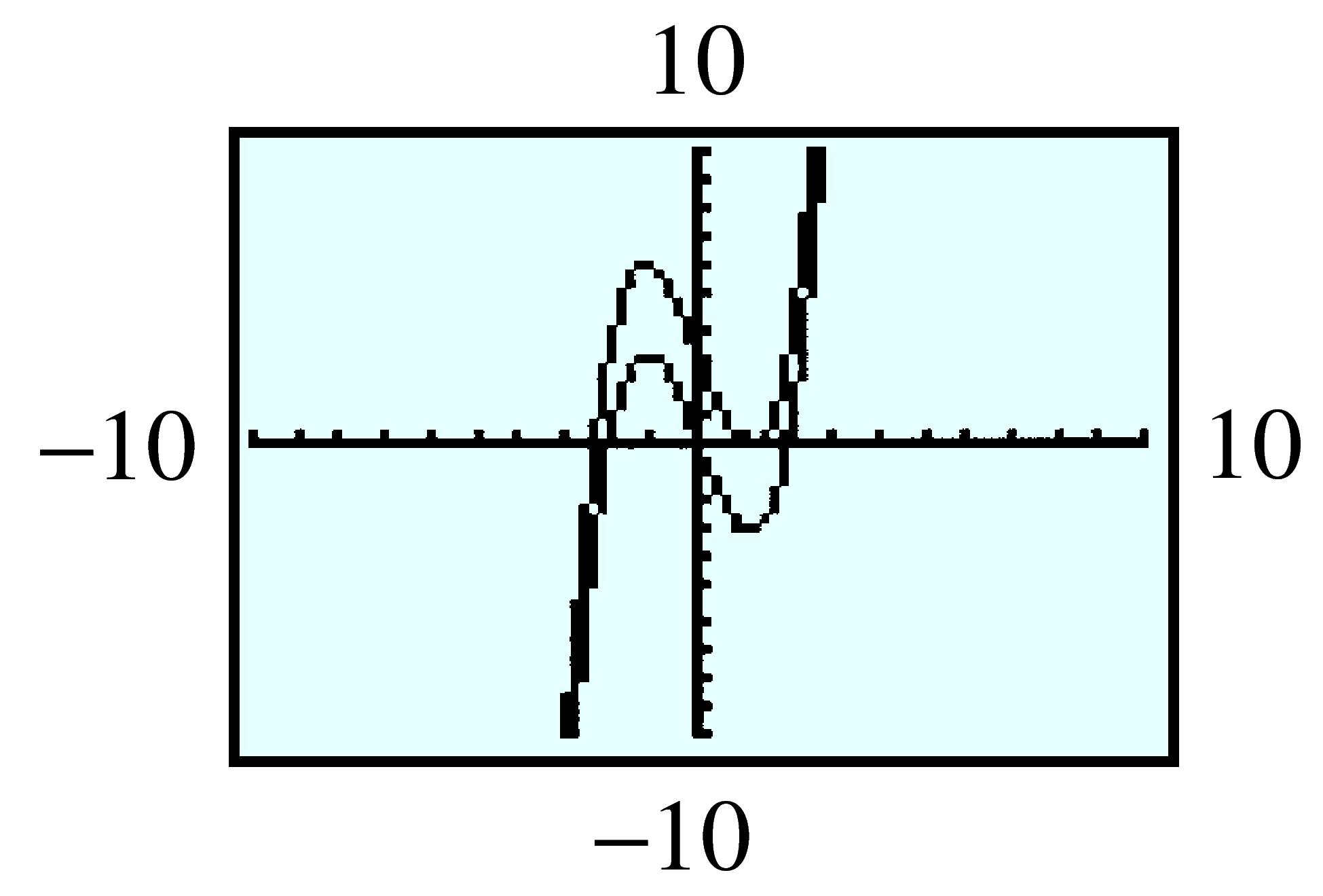
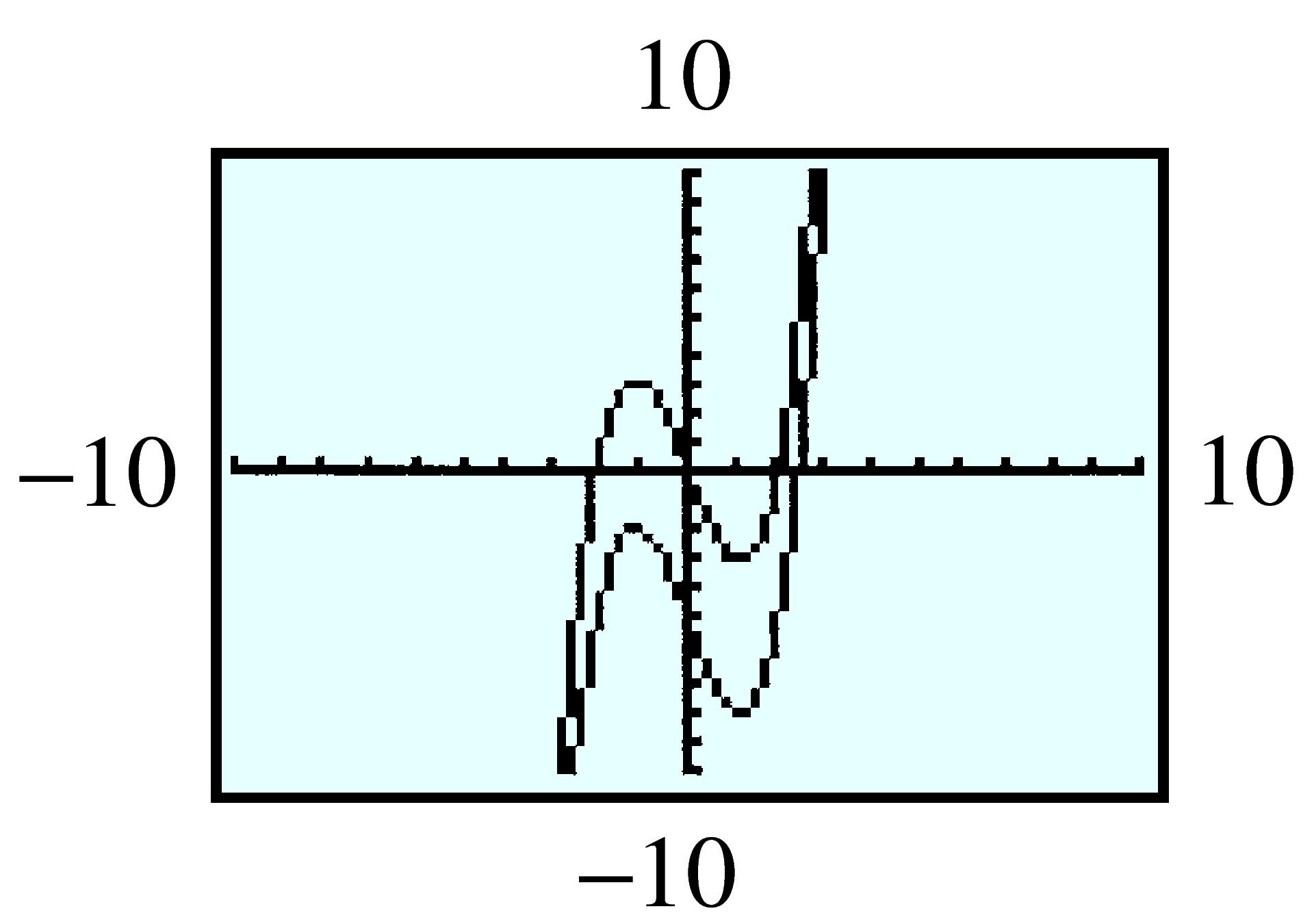
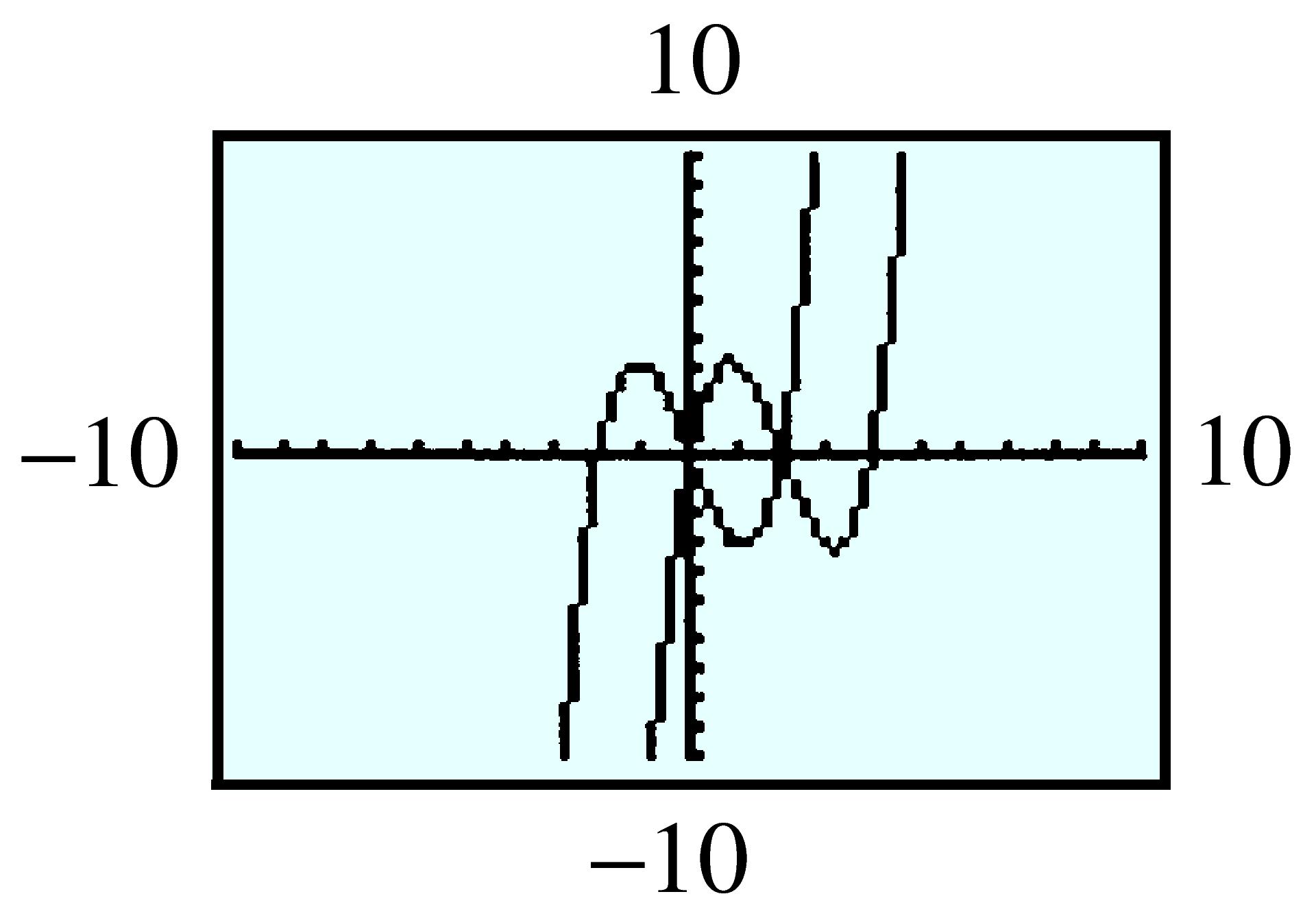
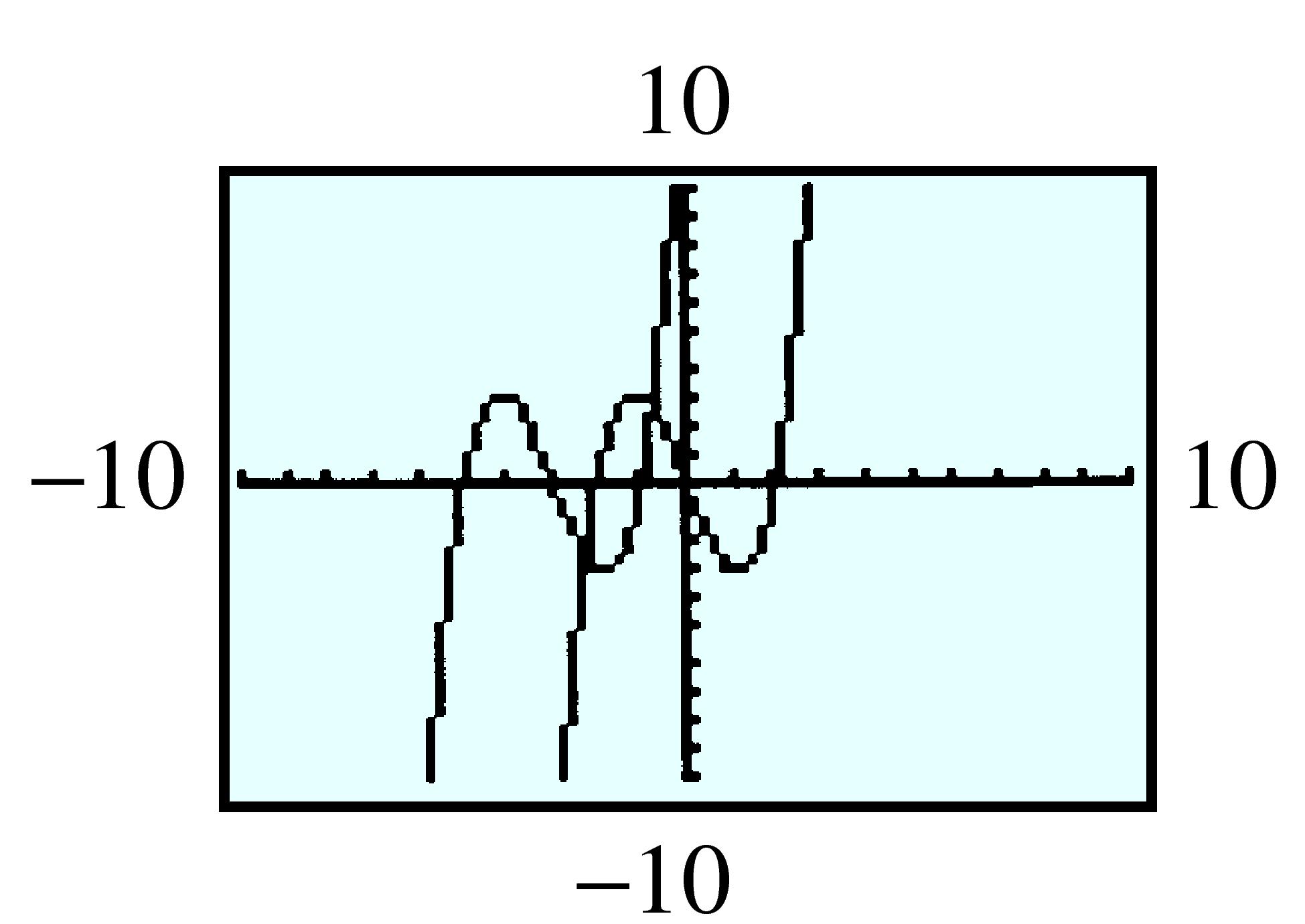
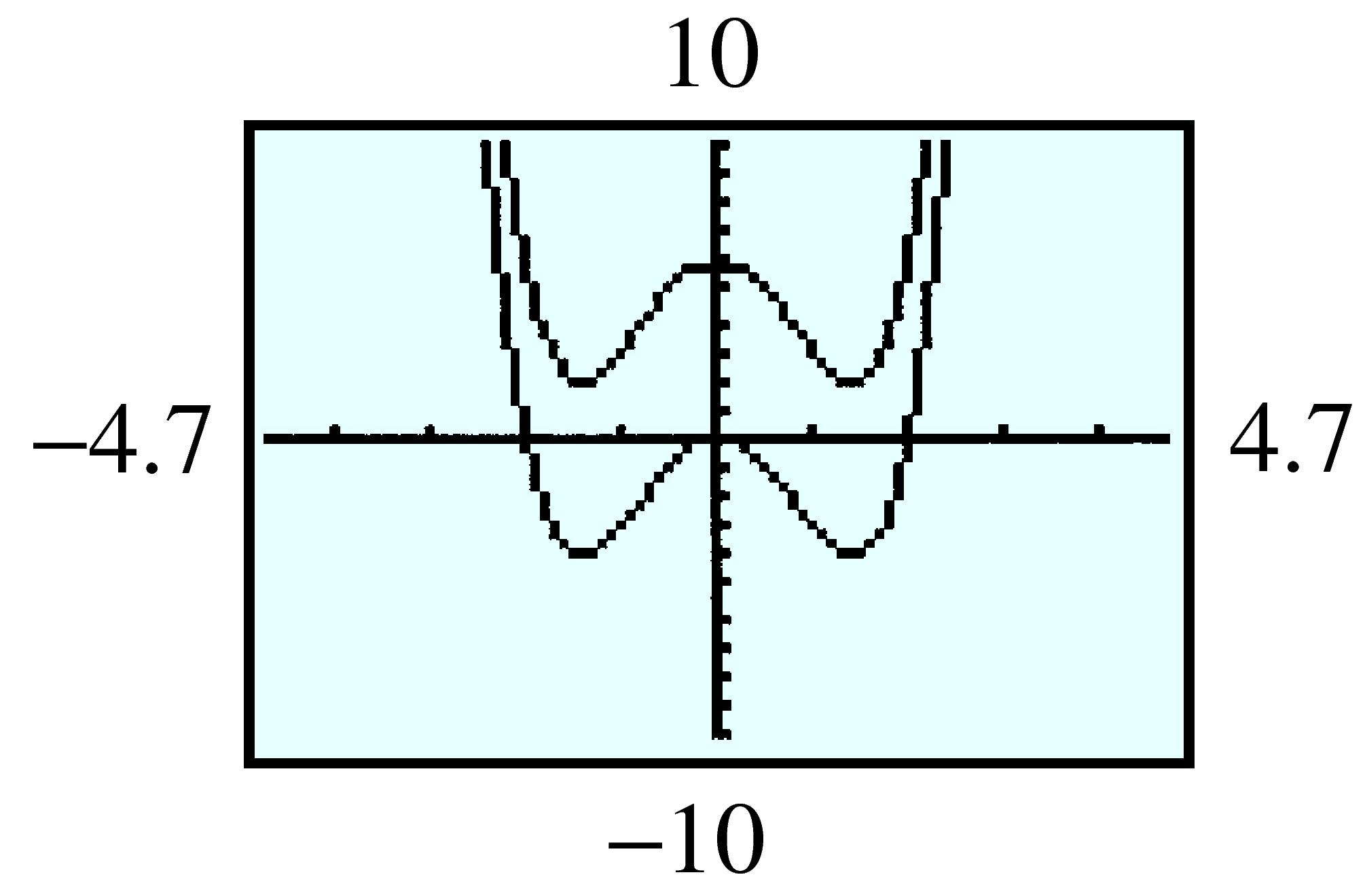
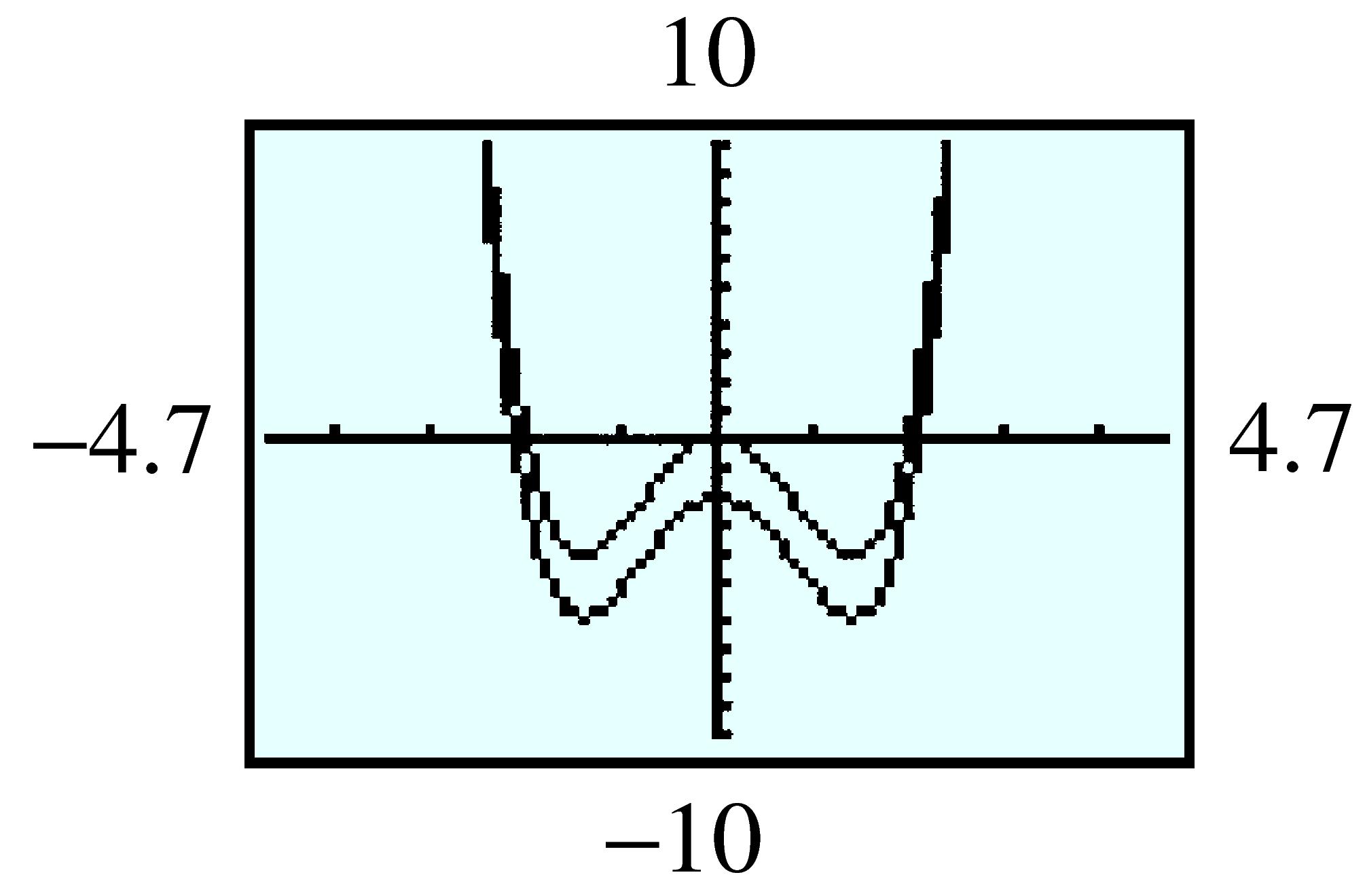
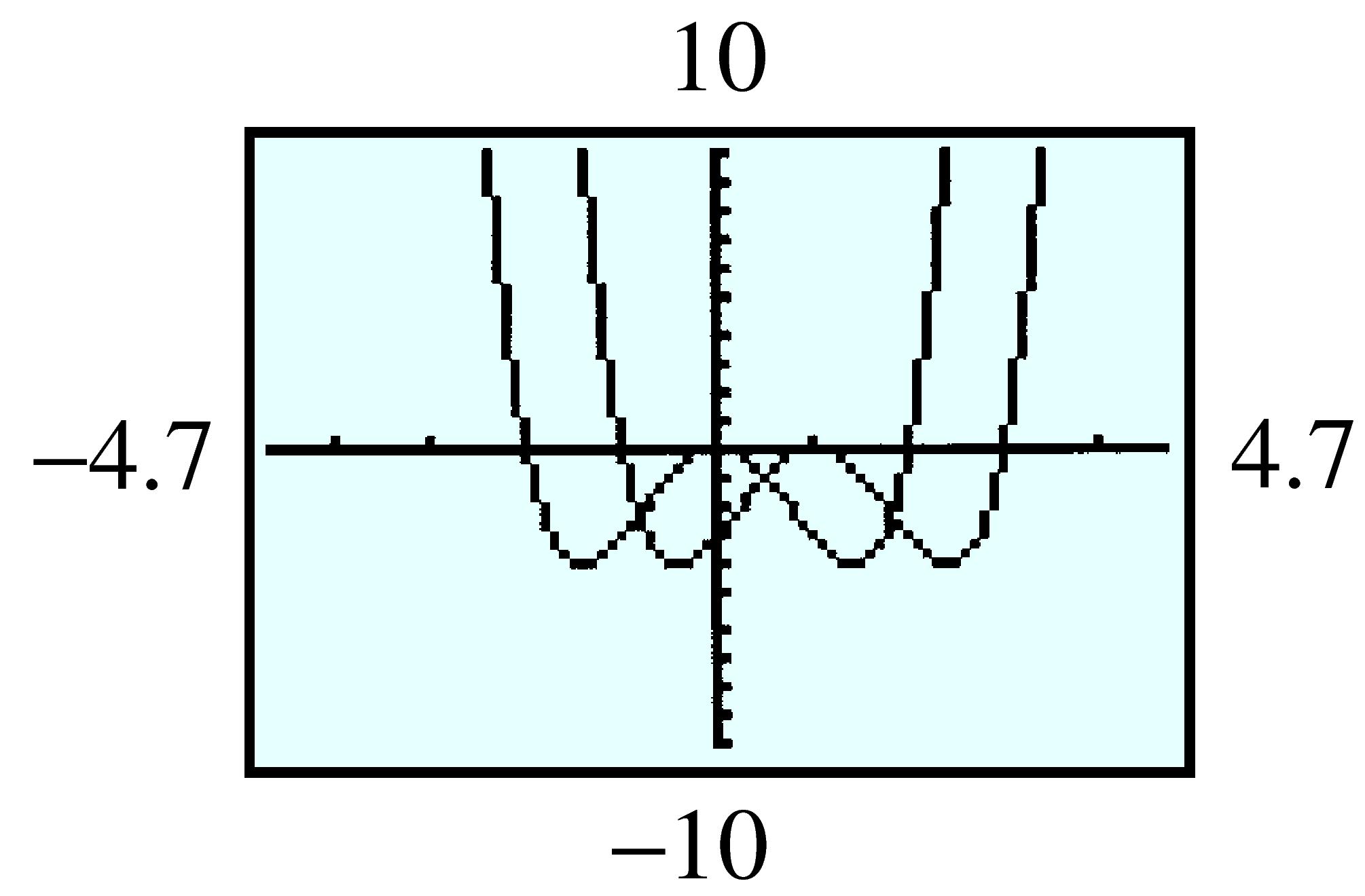
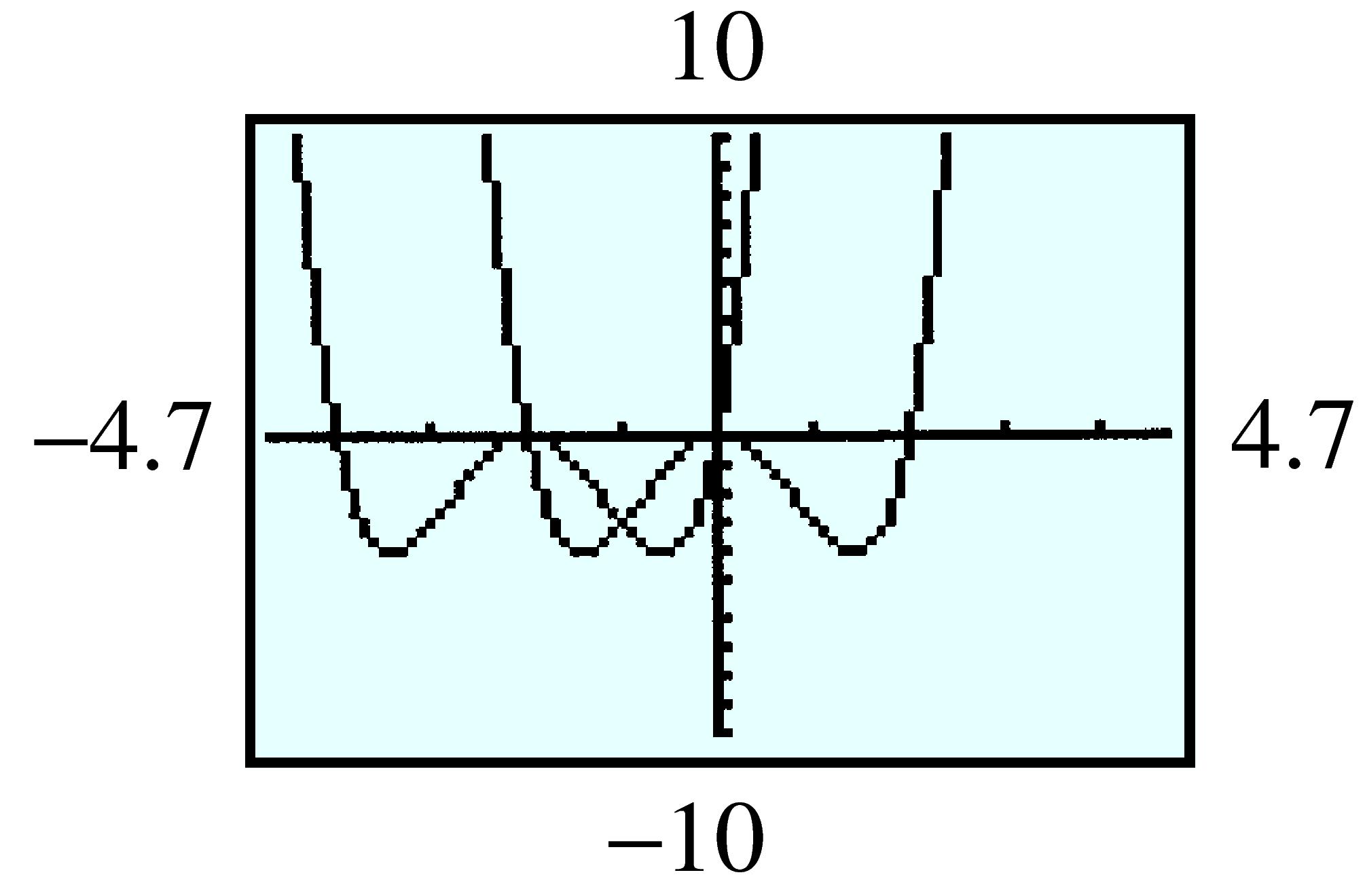
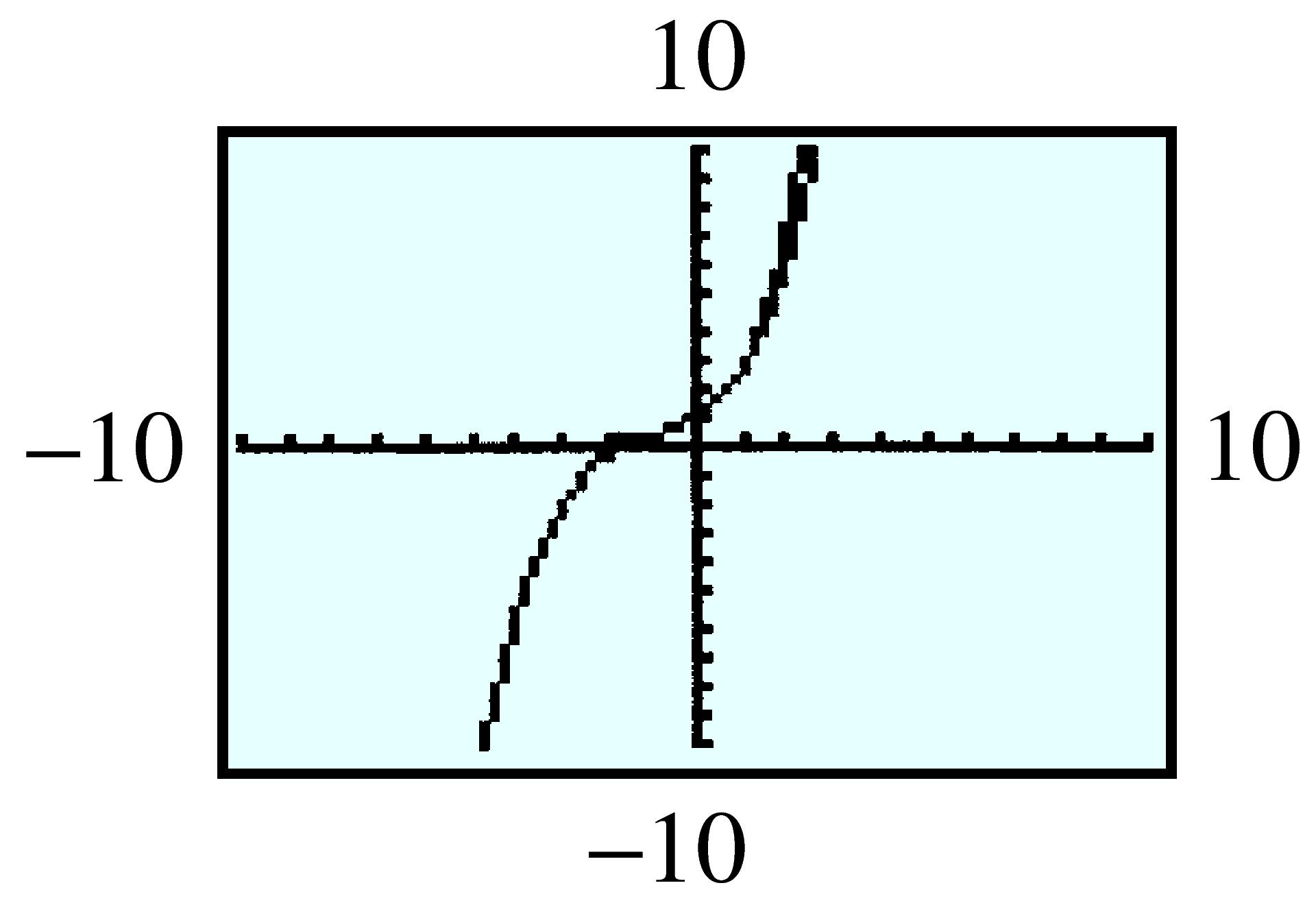
$x$	$-1$	$-0.5$	$0$	$0.5$	$1$	$1.5$	$2$
$f(x) $	$0.368 $	$0.607 $	$1 $	$1.649 $	$2.718 $	$4.482 $	$7.389 $
$p(x) $	$0.333$	$0.604$	$1$	$1.646$	$2.667$	$4.188$	$6.333$

$\displaystyle 0.122$
The error is relatively small for values of $x$ between $-3$ and $2.5\text{.}$

7.3 Complex Numbers
Homework 7.3

1.

Answer.

$-4+5i$

3.

Answer.

$-4+i$

5.

Answer.

$\dfrac{-5}{6}- \dfrac{\sqrt{2}}{6} i$

7.

Answer.

$-3\pm 2i$

9.

Answer.

$\dfrac{1}{6} \pm\dfrac{\sqrt{11}}{6} i$

11.

Answer.

$13 + 4i$

13.

Answer.

$-0.8 + 3.8i$

15.

Answer.

$20 + 10i$

17.

Answer.

$-17 + 34i$

19.

Answer.

$46 + 14i\sqrt{3}$

21.

Answer.

$52 $

23.

Answer.

$-2 - 2i $

25.

Answer.

$-1 + 4i$

27.

Answer.

$7+4i$

29.

Answer.

$\dfrac{-25}{29}+\dfrac{10}{29}i $

31.

Answer.

$\dfrac{3}{4} - \dfrac{\sqrt{3}}{4}i $

33.

Answer.

$\dfrac{-2}{3} + \dfrac{\sqrt{5}}{3}i $

35.

Answer.

$i $

37.

Answer.

$\displaystyle 0$
$\displaystyle 0$

39.

Answer.

$\displaystyle 0$
$\displaystyle 0$

41.

Answer.

$\displaystyle 0$
$\displaystyle 0$

43.

Answer.

$4z^2 + 49$

45.

Answer.

$x^2 + 6x + 10$

47.

Answer.

$v^2 - 8v + 17$

49.

Answer.

$x\ge 5\text{;}$ $~x\lt 5$

51.

Answer.

$\displaystyle -1$
$\displaystyle 1$
$\displaystyle -i$
$\displaystyle -1$

53.

Answer.

$\displaystyle 2-\sqrt{5}$
$\displaystyle x^2 - 4x - 1$

55.

Answer.

$\displaystyle 4+3i$
$\displaystyle x^2 - 8x +25$

57.

Answer.

$\displaystyle 4$
$\displaystyle 5$

59.

Answer.

$x^4 - 6x^3 + 23x^2 - 50x + 50$

61.

Answer.

$x^4 - 7x^3 + 20x^2 - 19x + 13$

63.

Answer.

The complex conjugates are reflections of each other across the real axis.

65.

Answer.

The complex conjugates are reflections of each other across the real axis.

67.

Answer.

69.

Answer.

71.

Answer.

$\displaystyle m=\dfrac{b}{a} $
$\displaystyle m=\dfrac{a}{-b} $
$-1\text{;}$ The angle is $90\degree\text{.}$

7.4 Graphing Rational Functions
Homework 7.4

1.

Answer.

$\displaystyle t=\dfrac{150}{50-v} $
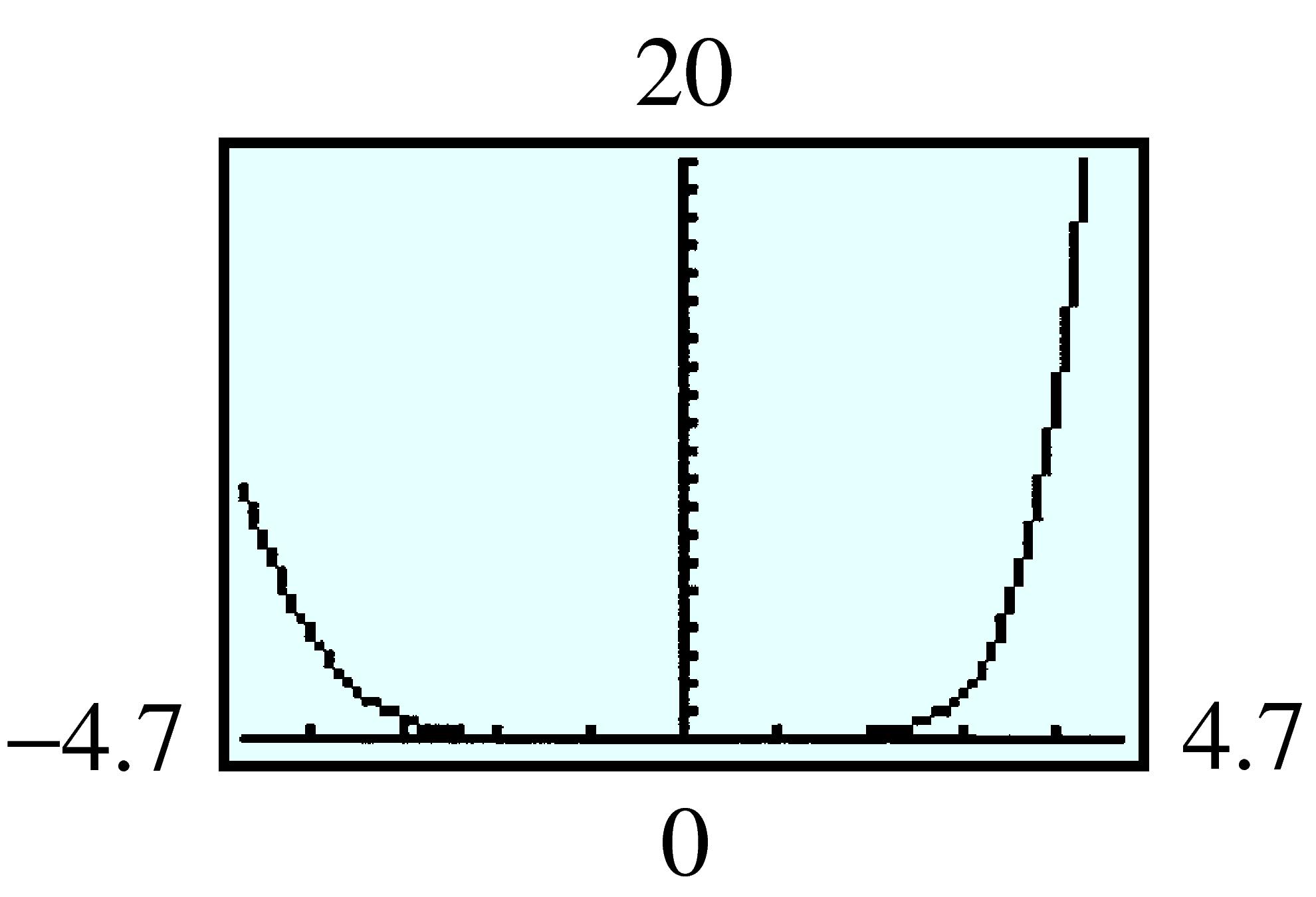
$v$ $0$ $5$ $10$ $15$ $20$ $25$ $30$ $35$ $40$ $45$ $50$

$t$ $3$ $3.33$ $3.75 $ $4.29 $ $5 $ $6 $ $7.5 $ $10 $ $15 $ $30 $ —

The travel time increases as the headwind speed increases.

3.

Answer.

$\displaystyle 0\le p \lt 100 $
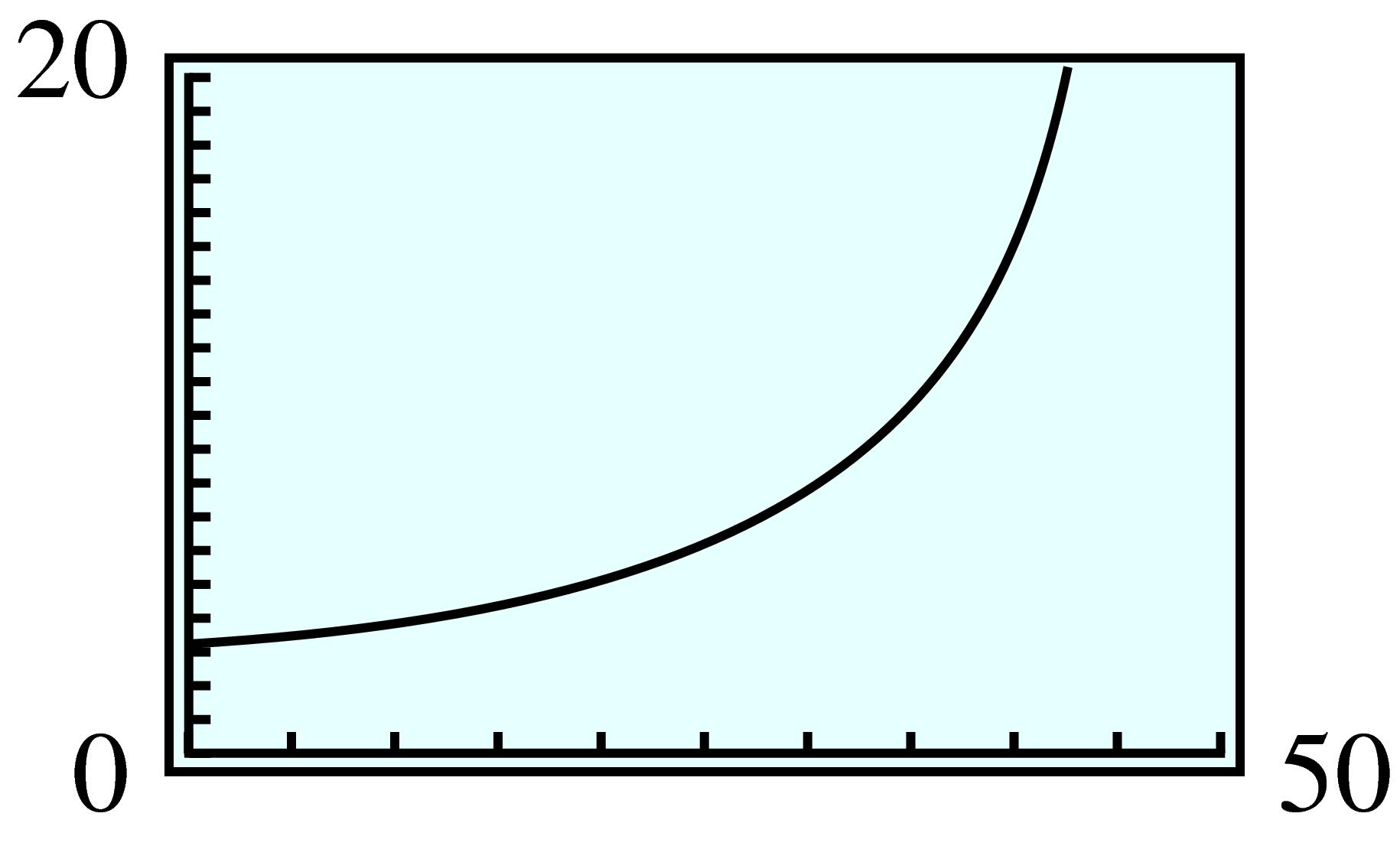
$p$ $0$ $15$ $25$ $40$ $50$ $75$ $80$ $90$ $100$

$C$ $0$ $12.7$ $24 $ $48 $ $72 $ $216 $ $288 $ $648 $ —
$\displaystyle 60\%$
$\displaystyle p\gt 96\%$
$p=100\text{;}$ As the percentage immunized approaches $100\text{,}$ the cost grows without bound.

5.

Answer.

$\displaystyle C=8+\dfrac{20,000}{n} $
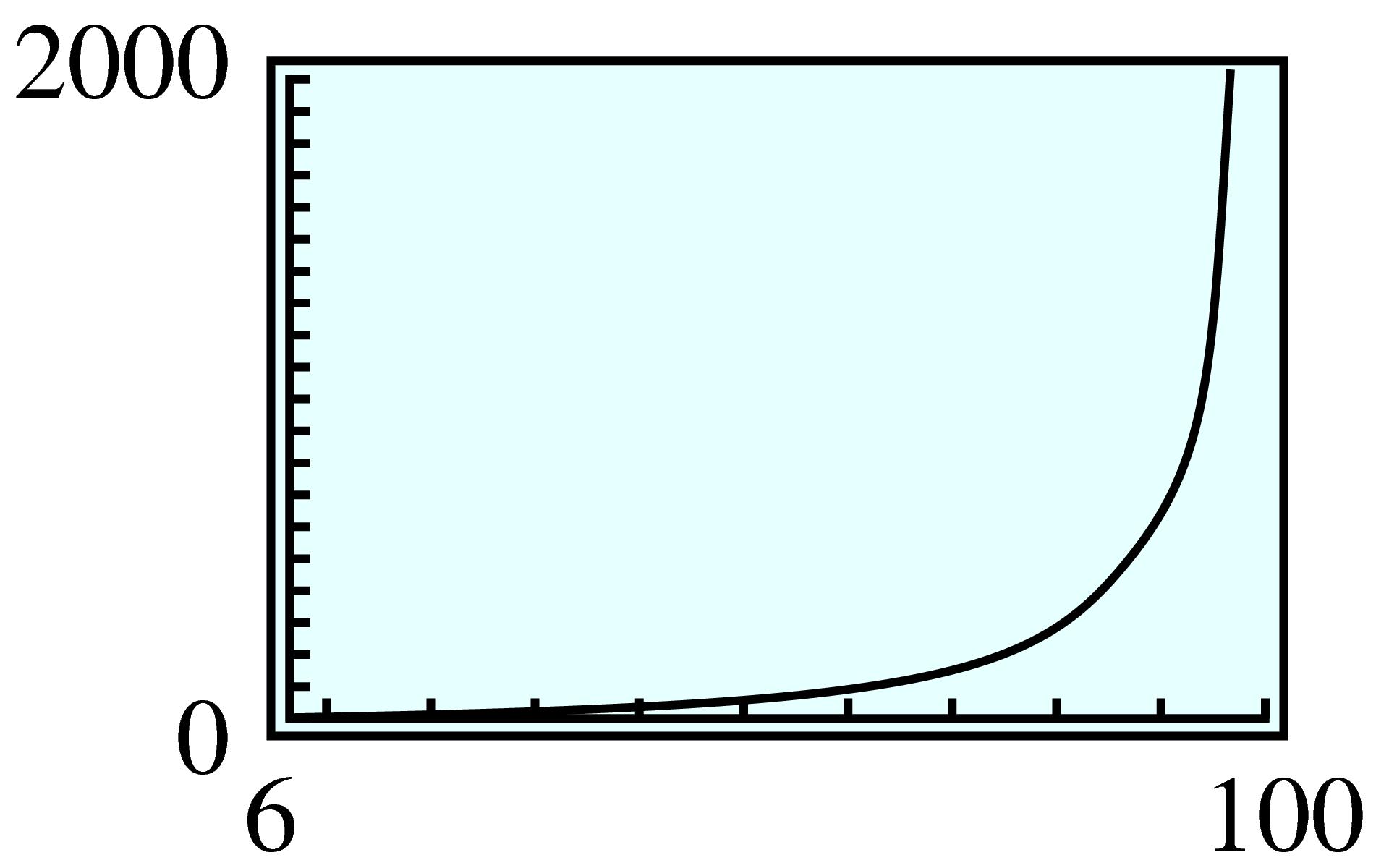
$n$ $100$ $200$ $400$ $500$ $1000$ $2000$ $4000$ $5000$ $8000$

$C$ $208 $ $108 $ $58 $ $48 $ $28 $ $18 $ $13 $ $12 $ $10.5 $
$\displaystyle 2000$
$\displaystyle n\gt 5000$
$C=8\text{;}$ As $n$ increases, the average cost per calculator approaches $$8\text{.}$

7.

Answer.

$4500+\dfrac{3000}{x} \text{;}$ $C(x) = 6x + 4500 + \dfrac{3000}{x} $
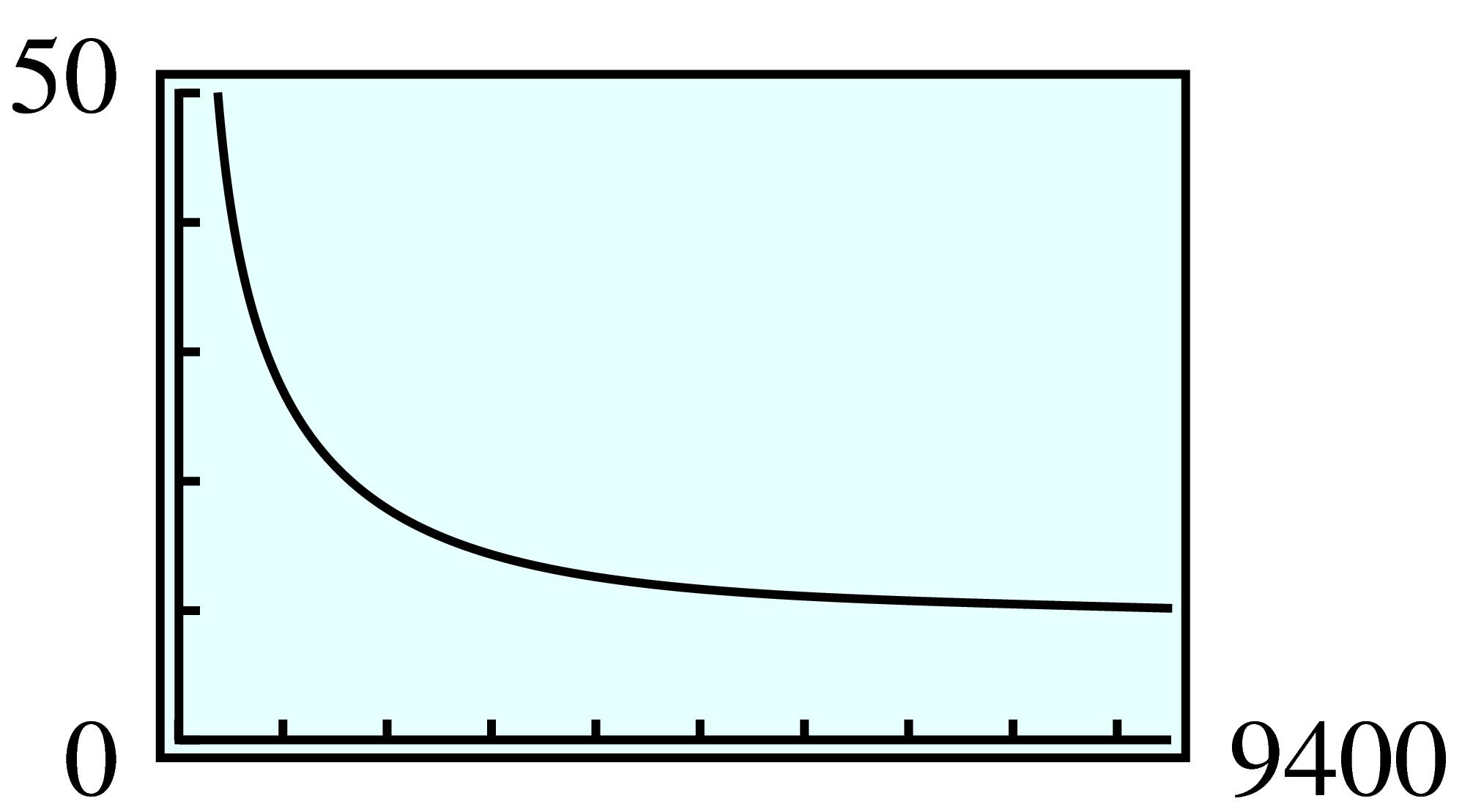
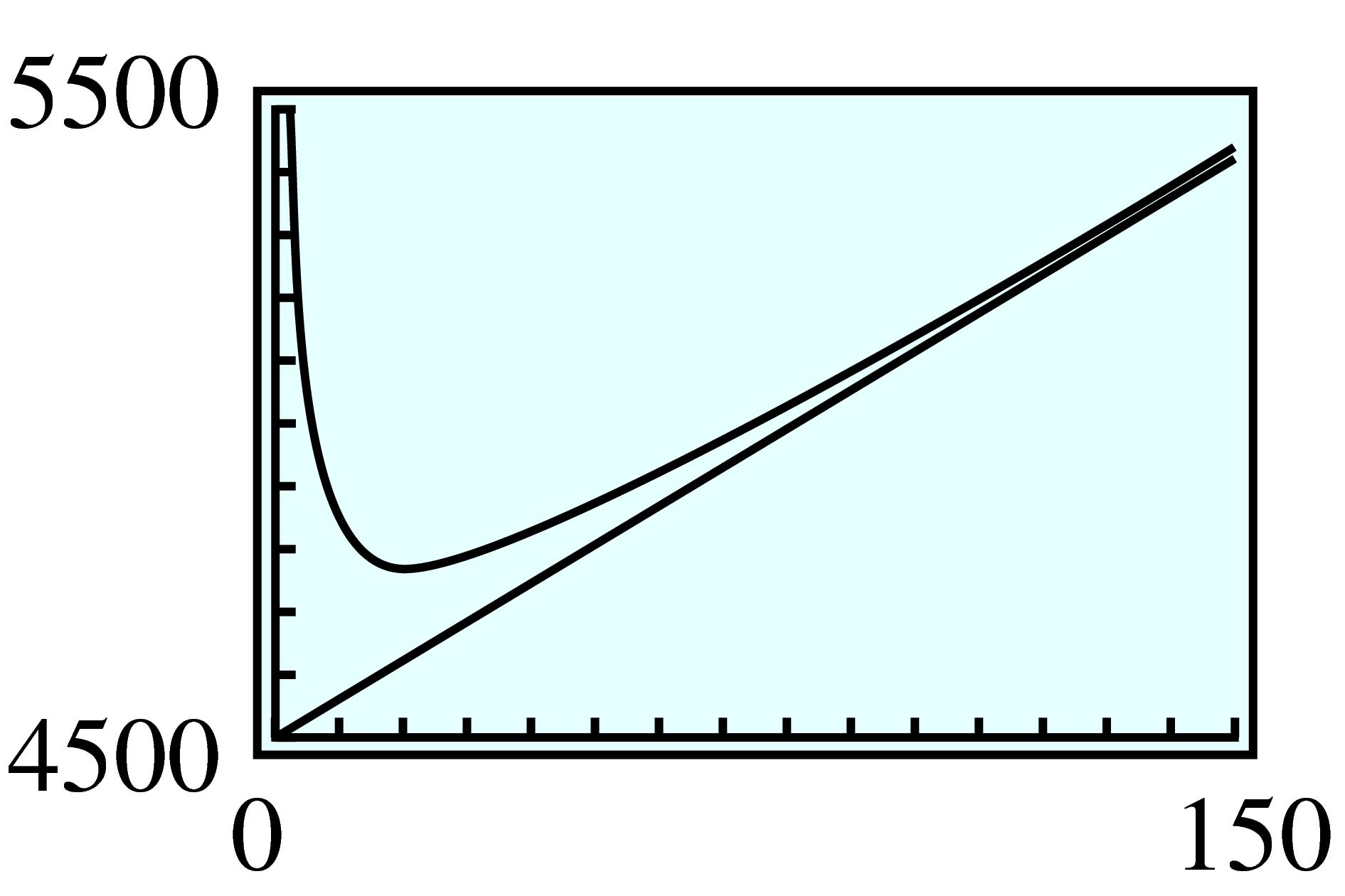
$x$ $10$ $20$ $30$ $40$ $50$ $60$ $70$ $80$ $90$ $100$

$C$ $4860 $ $4770 $ $4780 $ $4815 $ $4860 $ $4910 $ $5018 $ $5073 $ $5130 $
$$4768.33$
$22\text{;}$ $14$
The graph of $C$ approaches the line as an asymptote.

9.

Answer.

The surface area is $2x^2 + 4xh = 96\text{.}$ Solving for $h\text{,}$ $h=\dfrac{96-2x^2}{4x}=\dfrac{24}{x}-\dfrac{x}{2} \text{.}$
$\displaystyle V=24x-\dfrac{1}{2}x^3$
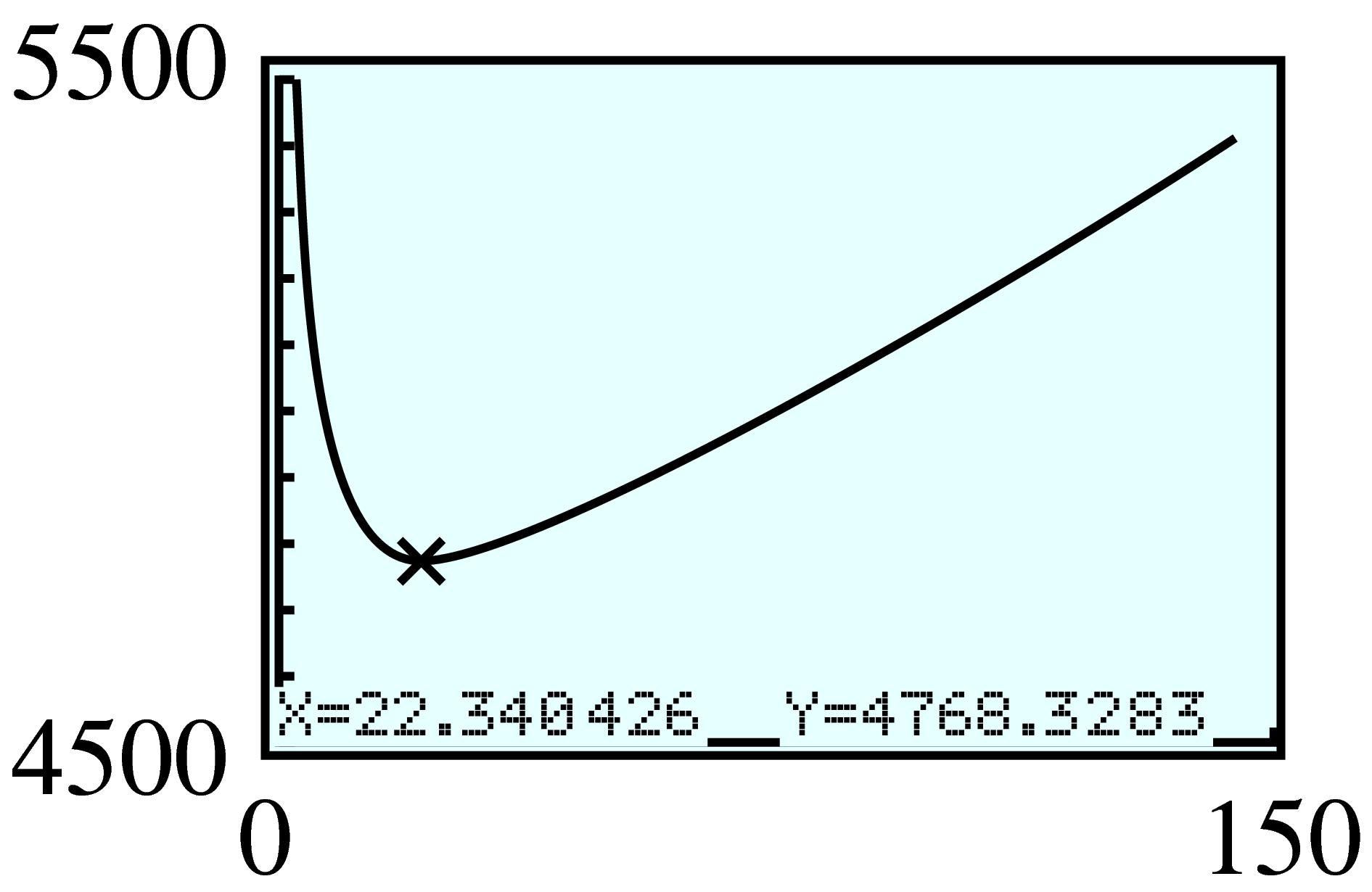
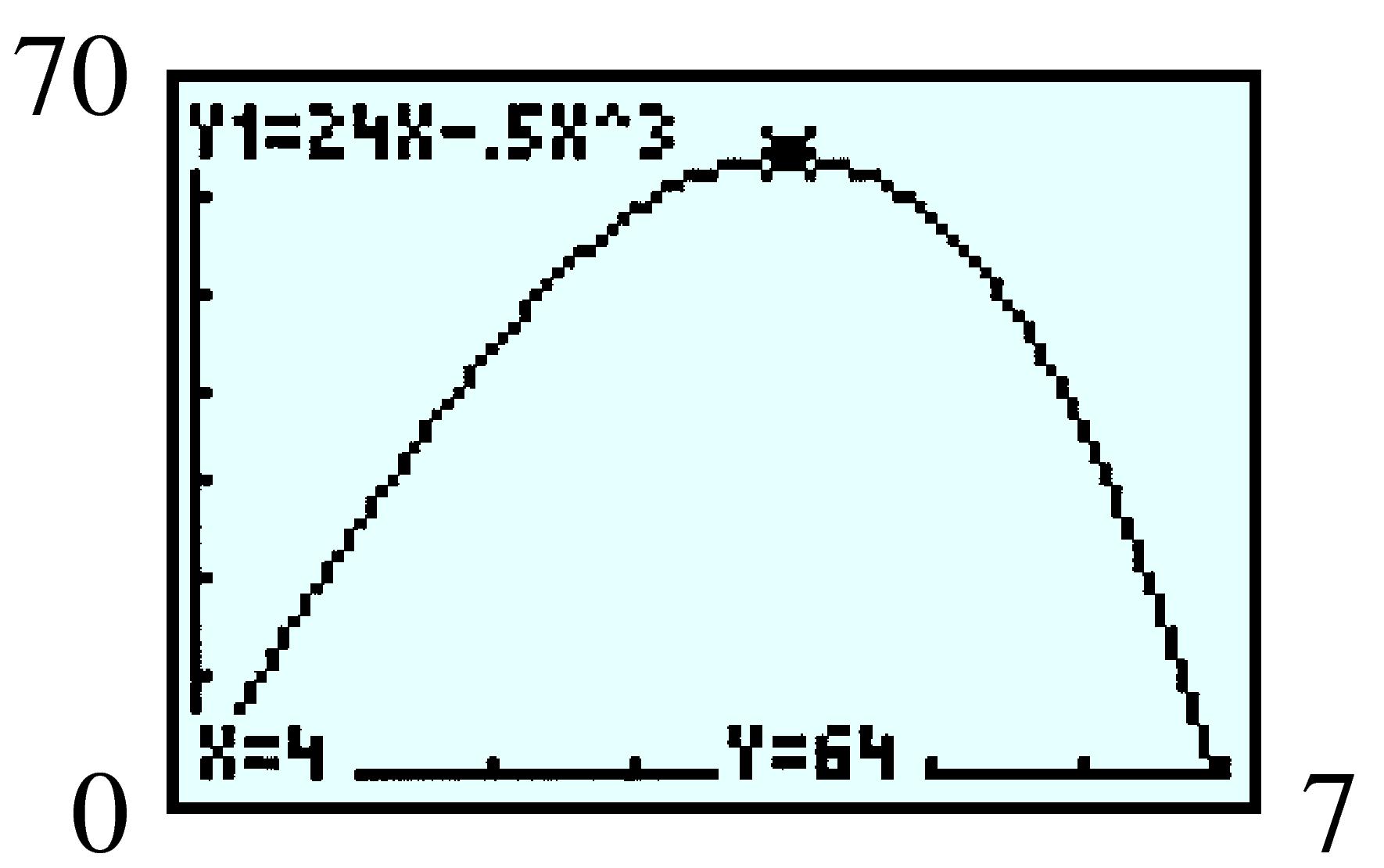
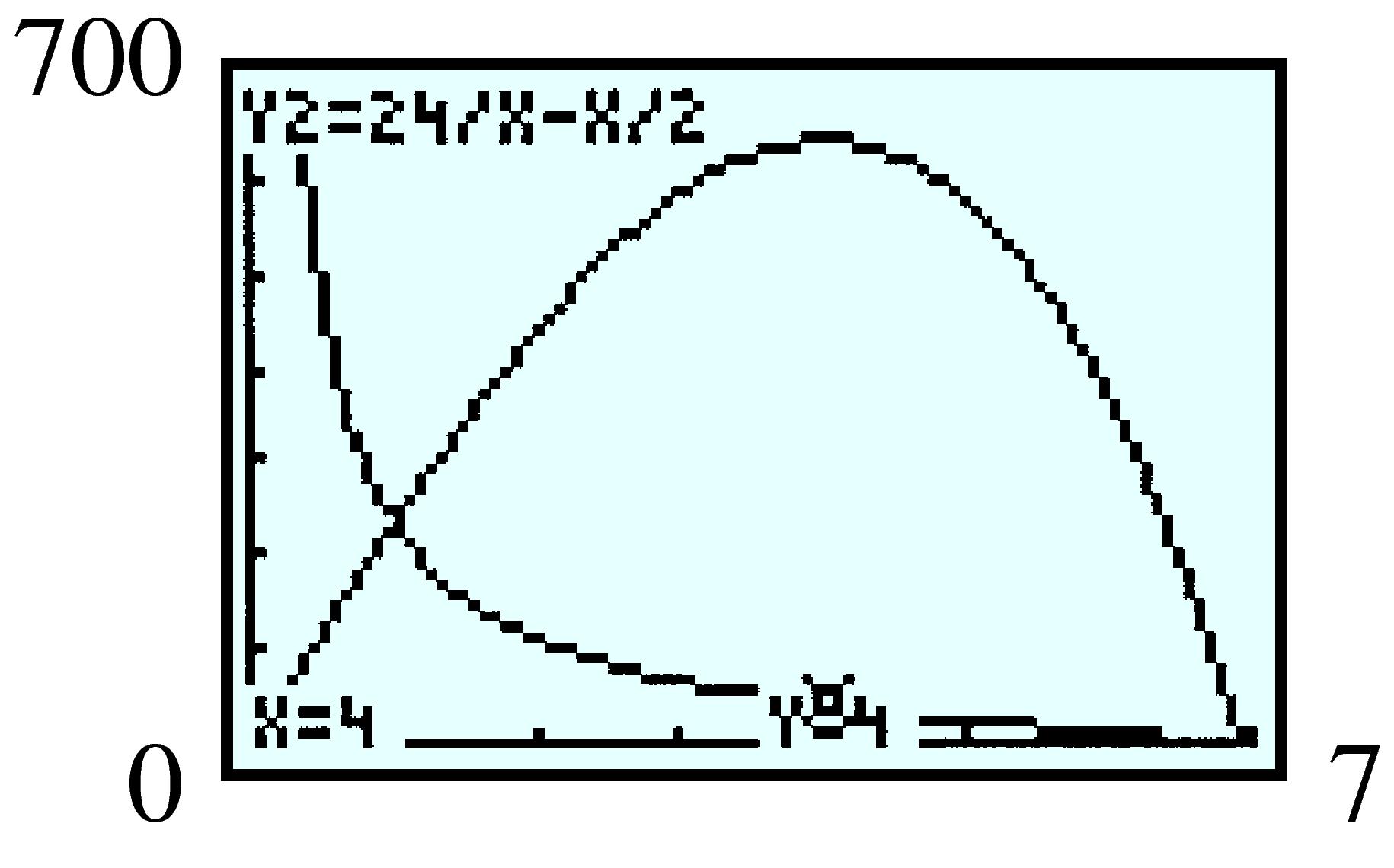
$x$ $1$ $2$ $3$ $4$ $5$ $6$ $7$

$h$ $23.5 $ $11 $ $6.5 $ $4$ $2.3 $ $1 $ $-0.07 $

$V$ $23.5 $ $44 $ $58.5 $ $64 $ $57.5 $ $36$ $-3.5 $

If the base is more than $7$ cm, the top and bottom alone exceed the total area allowed.
Maximum of $64$ cu. cm
$4$ cm
$h=4$ cm

11.

Answer.

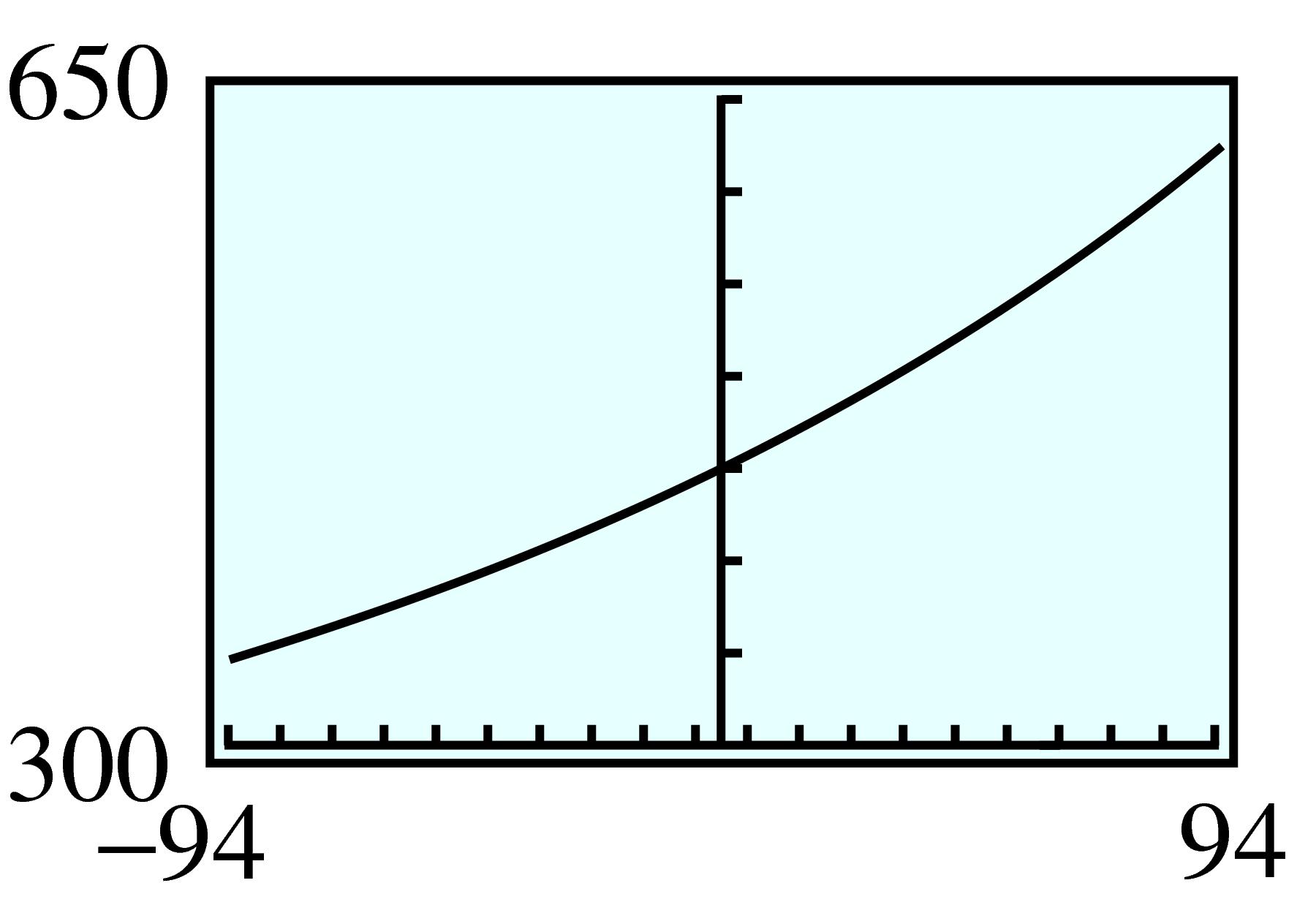
$v$ $-100$ $-75$ $-50$ $-25$ $0$ $25$ $50$ $75$ $100$

$P$ $338.15 $ $358.92 $ $382.41 $ $409.19 $ $440 $ $475.83 $ $518.01 $ $568.4 $ $629.66 $
$-20$ m/sec; $68$ m/sec
$v \gt 12$ m/sec
$v=332\text{;}$ As $v$ approaches $332$ m per sec, the pitch increases without bound.

13.

Answer.

15.

Answer.

17.

Answer.

19.

Answer.

21.

Answer.

23.

Answer.

25.

Answer.

27.

Answer.

29.

Answer.

31.

Answer.

33.

Answer.

$\displaystyle y=\dfrac{2}{x}+2$

35.

Answer.

$\displaystyle y=\dfrac{1}{x+1}+1$

37.

Answer.

$\displaystyle y=\dfrac{1}{(x-2)^2}+3$

39.

Answer.

$\displaystyle \dfrac{25}{s+8} $
$\displaystyle \dfrac{25}{s-8} $
$\displaystyle \dfrac{50s}{s^2-64} $

41.

Answer.

$\displaystyle \dfrac{900}{400+w} $
$\displaystyle \dfrac{900}{400-w} $
Orville by $\dfrac{1800w}{160,000-w^2} $ hours

43.

Answer.

$\displaystyle \dfrac{1}{f}=\dfrac{2q+60}{q^2+60q} $
$\displaystyle f=\dfrac{q^2+60q}{2q+60} $

45.

Answer.

$\dfrac{1}{y}=\dfrac{1}{x}+\dfrac{1}{k}=\dfrac{k+x}{xk}\text{,}$ so by taking reciprocals, $y=\dfrac{kx}{x+k} \text{.}$
The graphs increase from the origin and approach a horizontal asymptote at $y=k\text{.}$

47.

Answer.

$\dfrac{12x}{x+20} $

49.

Answer.

$\displaystyle V$
$\displaystyle \dfrac{V}{2} $
$V\approx0.7, ~K\approx 2.2$ (many answers are possible)
(See figure.)

51.

Answer.

$\dfrac{1}{v}=\dfrac{K}{V}\cdot\dfrac{1}{s} +\dfrac{1}{V}\text{;}$ Therefore, $a=\dfrac{K}{V} $ and $b=\dfrac{1}{V} $
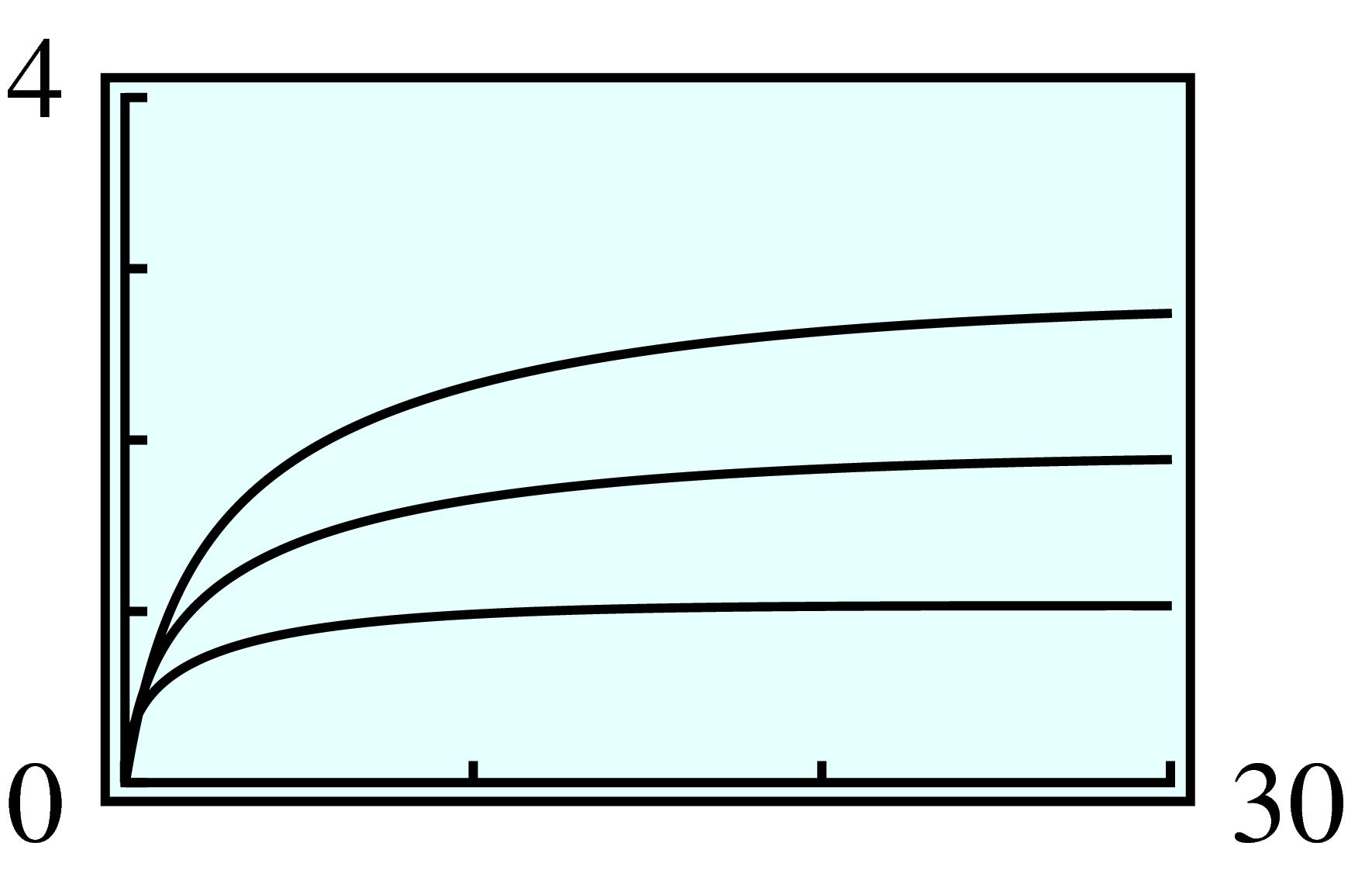
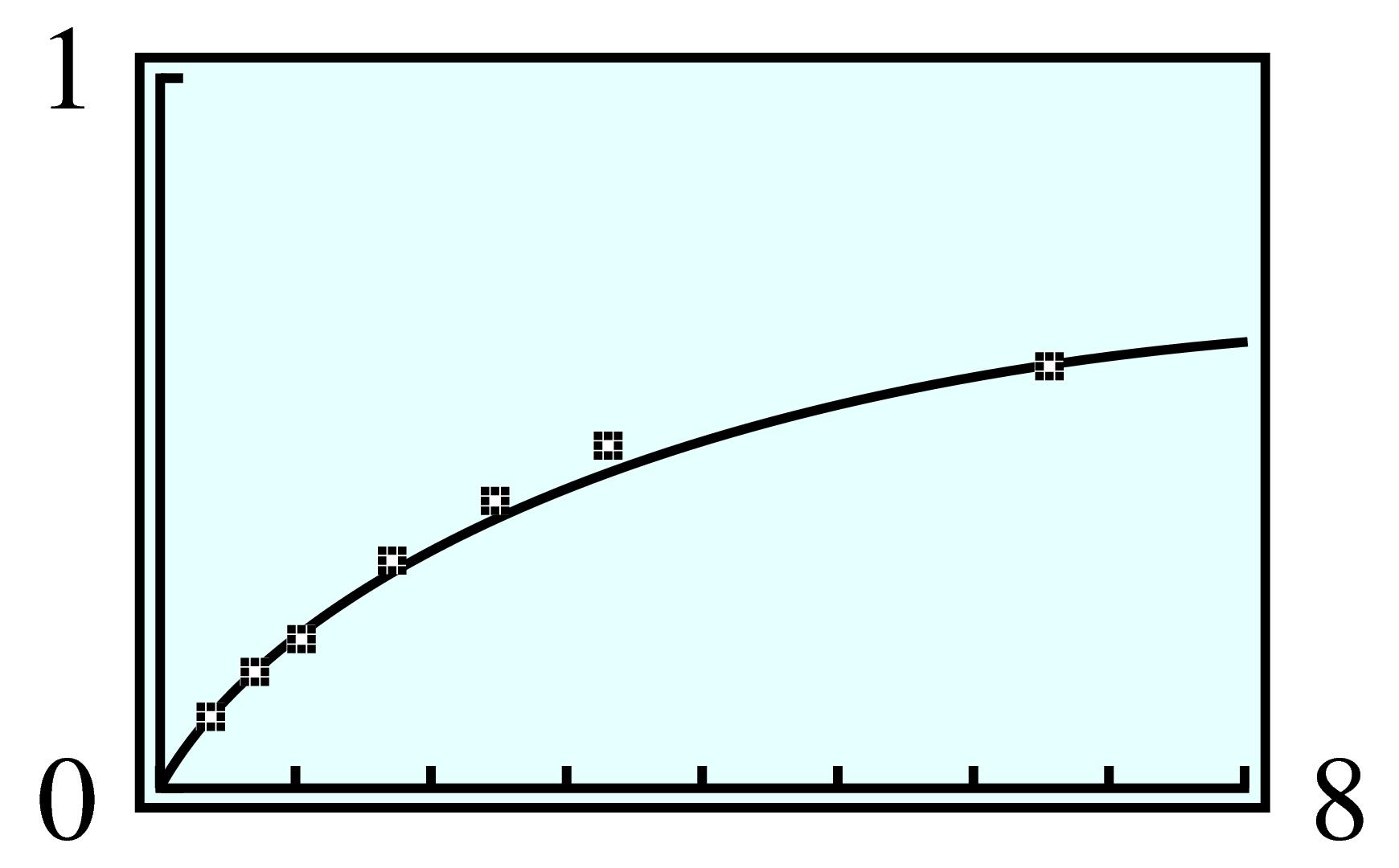
$\frac{1}{s}$ $3$ $1.5$ $1$ $0.6$ $0.4$ $0.3$ $0.15$

$\frac{1}{v} $ $12.5$ $7.1$ $5$ $3.3$ $2.6$ $2.2$ $1.7$
$\displaystyle \dfrac{1}{v}=3.8\cdot \dfrac{1}{s}+1.1 $
$\displaystyle V\approx 0.89, ~K\approx 3.37$

53.

Answer.

$\displaystyle x\ne 2$
$\displaystyle x+2$

55.

Answer.

$\displaystyle x\ne \pm 1$
$\displaystyle \dfrac{1}{x-1} $

7.5 Equations That Include Algebraic Fractions
Homework 7.5

1.

Answer.

$\dfrac{-1}{2} $

3.

Answer.

$\dfrac{13}{8} $

5.

Answer.

$\pm\sqrt{\dfrac{15}{8}} $

7.

Answer.

$\dfrac{1800}{1849}\approx 0.97 $

9.

Answer.

$37$ ft

11.

Answer.

$\displaystyle t=\dfrac{150}{50-v} $
$4=\dfrac{150}{50-v} \text{;}$ $v=12.5$ mph

13.

Answer.

$168=\dfrac{72p}{100-p}\text{;}$ $p=70\%$

15.

Answer.

$\displaystyle x=1$

17.

Answer.

$\displaystyle x=\dfrac{1}{2} $

19.

Answer.

$$2.50$
$\dfrac{160}{x}=6x+49 \text{;}$ $x=2.50$

21.

Answer.

$\displaystyle L=\dfrac{3200}{w} $
$\displaystyle P=\dfrac{6400}{w}+2w $
Lowest point: $(56.6, 226)\text{;}$ The minimum perimeter is $226$ ft for a width of $56.6$ ft.
$\displaystyle 240=\dfrac{6400}{w}+2w$
$40$ ft by $80$ ft

23.

Answer.

Multiply both sides of the equation by $bd$ and simplify.

\begin{equation*} \frac{a}{b}\cdot \frac{bc}{1} = \frac{c}{d} \cdot \frac{bc}{1}, \text{ so } ac=bd \end{equation*}

25.

Answer.

$4$

27.

Answer.

$40$

29.

Answer.

$$6187.50$

31.

Answer.

$45$ mi

33.

Answer.

$689$

35.

Answer.

$19,882$ m
$\displaystyle 0.3\%$
$0.00657$ in

37.

Answer.

$\displaystyle AE = 1,~ DE = x - 1,~ CD = 1$
$\displaystyle \dfrac{1}{x}=\dfrac{x-1}{x} $
$\displaystyle \dfrac{1+\sqrt{5}}{2} $

39.

Answer.

$r=\dfrac{S-a}{S} $

41.

Answer.

$x=\dfrac{Hy}{2y-H} $

43.

Answer.

$d=\pm \sqrt{\dfrac{Gm_1 m_2}{F}} $

45.

Answer.

$r=\dfrac{2QI}{I+Q} $

47.

Answer.

$P=\dfrac{ES}{E+S} $

49.

Answer.

$5$

51.

Answer.

$1$

53.

Answer.

$\dfrac{-14}{5} $

55.

Answer.

$\dfrac{-1}{6}, \dfrac{-4}{3} $

57.

Answer.

$\displaystyle t_1=\dfrac{144}{s-20} $
$\displaystyle t_2=\dfrac{144}{s+20} $
If the airspeed is $100$ mph, the round trip will take $3$ hours.
$\displaystyle \dfrac{144}{s-20}+\dfrac{144}{s+20}=3 $
$100$ mph

59.

Answer.

$\displaystyle t_1=\dfrac{d}{r_1}, ~t_2=\dfrac{d}{r_2} $
Total distance is $2d\text{;}$ total time $\dfrac{d}{r_1}+ \dfrac{d}{r_2} \text{.}$
$\displaystyle \dfrac{2d}{\dfrac{d}{r_1}+\dfrac{d}{r_2}} $
$\displaystyle \dfrac{2r_1 r_2}{r_1+r_2} $
$58\frac{1}{3}$ mph

7.6 Chapter Summary and Review
Chapter 7 Review Problems

1.

Answer.

$2x^3 - 11x^2 + 19x - 10 $

3.

Answer.

$t^3 + 3t^2 - 5t - 4$

5.

Answer.

$31x^2$

7.

Answer.

$-13x^3$

9.

Answer.

$(2x-3z)(4x^2+6xz+9z^2) $

11.

Answer.

$(y + 3x)(y^2 - 3xy + 9x^2) $

13.

Answer.

$v^3 - 30v^2 + 300v - 1000$

15.

Answer.

$\displaystyle \dfrac{1}{6}n^3-\dfrac{1}{2}n^2+\dfrac{1}{3}n $
$\displaystyle 220$
$\displaystyle 20$

17.

Answer.

$\displaystyle [-968, 972]$

19.

Answer.

$\displaystyle 2, -1$

21.

Answer.

$\displaystyle 0,1, -3$

23.

Answer.

$\displaystyle 0,1, -1$

25.

Answer.

$\displaystyle -1, 1$

27.

Answer.

$\displaystyle -1, 1, \pm\sqrt{6} $

29.

Answer.

$x(x + 2)(x - 3)$

31.

Answer.

$x^3(x + 2)(x - 2)$

33.

Answer.

$x^2(x + 4)(x - 4)$

35.

Answer.

$\displaystyle P(-2) = 0$
$\displaystyle \dfrac{3\pm\sqrt{13}}{2} $

37.

Answer.

$-2 \pm i \sqrt{6}$

39.

Answer.

$1 \pm \dfrac{\sqrt{6}}{3} i $

41.

Answer.

$\displaystyle -8$
$\displaystyle -8$

43.

Answer.

$\dfrac{11}{10}-\dfrac{13}{10}i $

45.

Answer.

$x^4 - 2x^3 + 14x^2 - 18x + 45$

47.

Answer.

49.

Answer.

$\displaystyle V=\dfrac{\pi h^3}{4} $
$2\pi\text{ cm}^3 \approx 6.28\text{ cm}^3 \text{;}$ $16\pi\text{ cm}^3 \approx 50.27\text{ cm}^3 $

51.

Answer.

$\displaystyle 338$
Months $2$ and $20$
During month $6\text{.}$ The number of members eventually decreases to zero.

53.

Answer.

All numbers except $-2, 0, 2\text{.}$

55.

Answer.

57.

Answer.

Horizontal asymptote $y = 0\text{;}$ Vertical asymptote $x = 4\text{;}$ $y$-intercept $(0,\frac{-1}{4} )$

59.

Answer.

Horizontal asymptote $y = 1\text{;}$ Vertical asymptote $x = -3\text{;}$ $x$-intercept $(2,0)\text{;}$ $y$-intercept $(0,\frac{-2}{3} )$

61.

Answer.

Horizontal asymptote $y = 3\text{;}$ Vertical asymptote $x = \pm 2\text{;}$ $x$-intercept $(0,0)\text{;}$ $y$-intercept $(0,0 )$

63.

Answer.

$\displaystyle y=\dfrac{-5}{x+3}+3 $

65.

Answer.

$\displaystyle y=\dfrac{2}{(x+1)^2}+1 $

67.

Answer.

$\displaystyle t_1=\dfrac{90}{v-2} $
$\displaystyle t_2=\dfrac{90}{v+2} $
$\displaystyle \dfrac{90}{v-2}+\dfrac{90}{v+2}=24 $
$8$ mph

69.

Answer.

$\dfrac{320}{x}=\dfrac{1}{2}x+6~\text{;}$ $$20$

71.

Answer.

$299$

73.

Answer.

$-2$

75.

Answer.

No solution

77.

Answer.

All $a$ except $-1$ and $1$

79.

Answer.

$0$

81.

Answer.

$n=\dfrac{Ct}{C-V} $

83.

Answer.

$q=\dfrac{pr}{r-p} $

8 Linear Systems
8.1 Systems of Linear Equations in Two Variables
Homework 8.1

1.

Answer.

$(3, 0) $

3.

Answer.

$(50,70) $

5.

Answer.

$(-2,3)$

7.

Answer.

$(2,3)$

9.

Answer.

$two lines$

Inconsistent

11.

Answer.

Consistent and independent

13.

Answer.

Dependent

15.

Answer.

Inconsistent

17.

Answer.

Consistent and independent

19.

Answer.

Dependent

21.

Answer.

$\displaystyle D = 10 + 0.09x$
$\displaystyle F = 15 + 0.05x$
$125$ min

23.

Answer.

$\displaystyle y = 50x$
$\displaystyle y = 2100 - 20x$
$30$¢ per bushel, $1500$ bushels

25.

Answer.

$\displaystyle C = 200 + 4x$
$\displaystyle R = 12x$
$25$ pendants

27.

Answer.

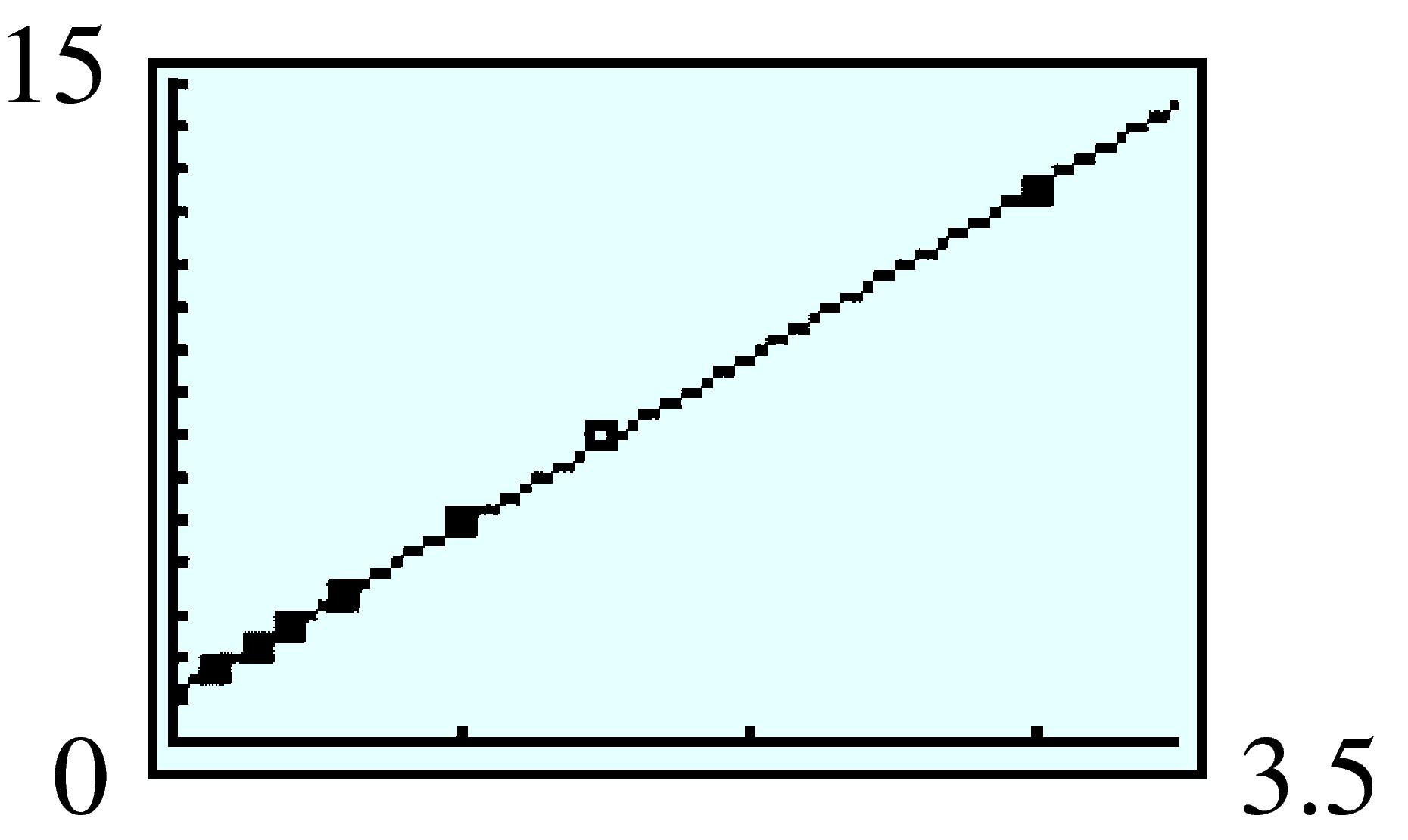
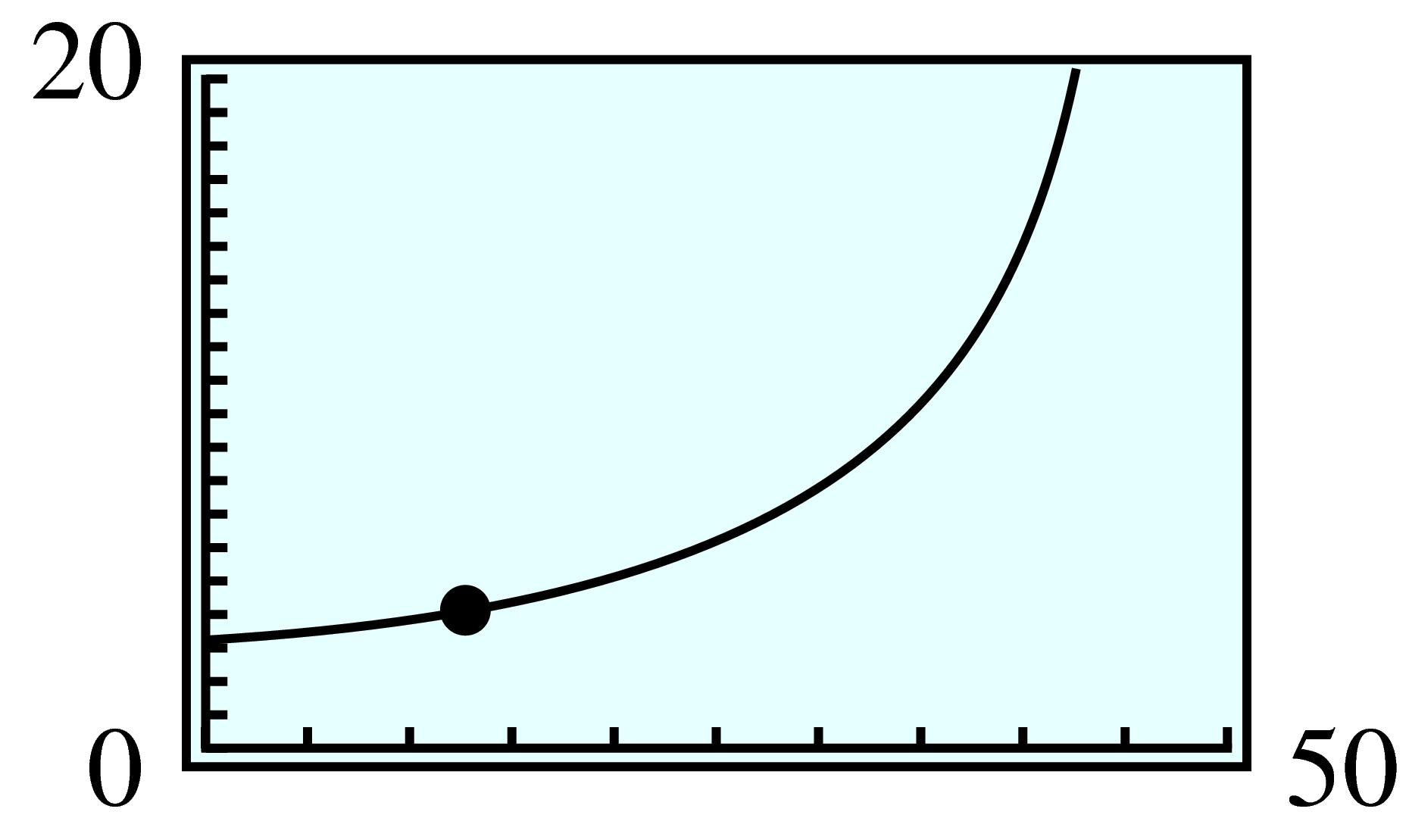
Number of
tickets Cost per
ticket Revenue

Adults $x$ $7.50$ $7.50x$

Students $y$ $4.25$ $4.25y$

Total $82$ — $465.50$
$\displaystyle x + y = 82$
$\displaystyle 7.50x + 4.25y = 465.50$
$36$ adults, $46$ students

29.

Answer.

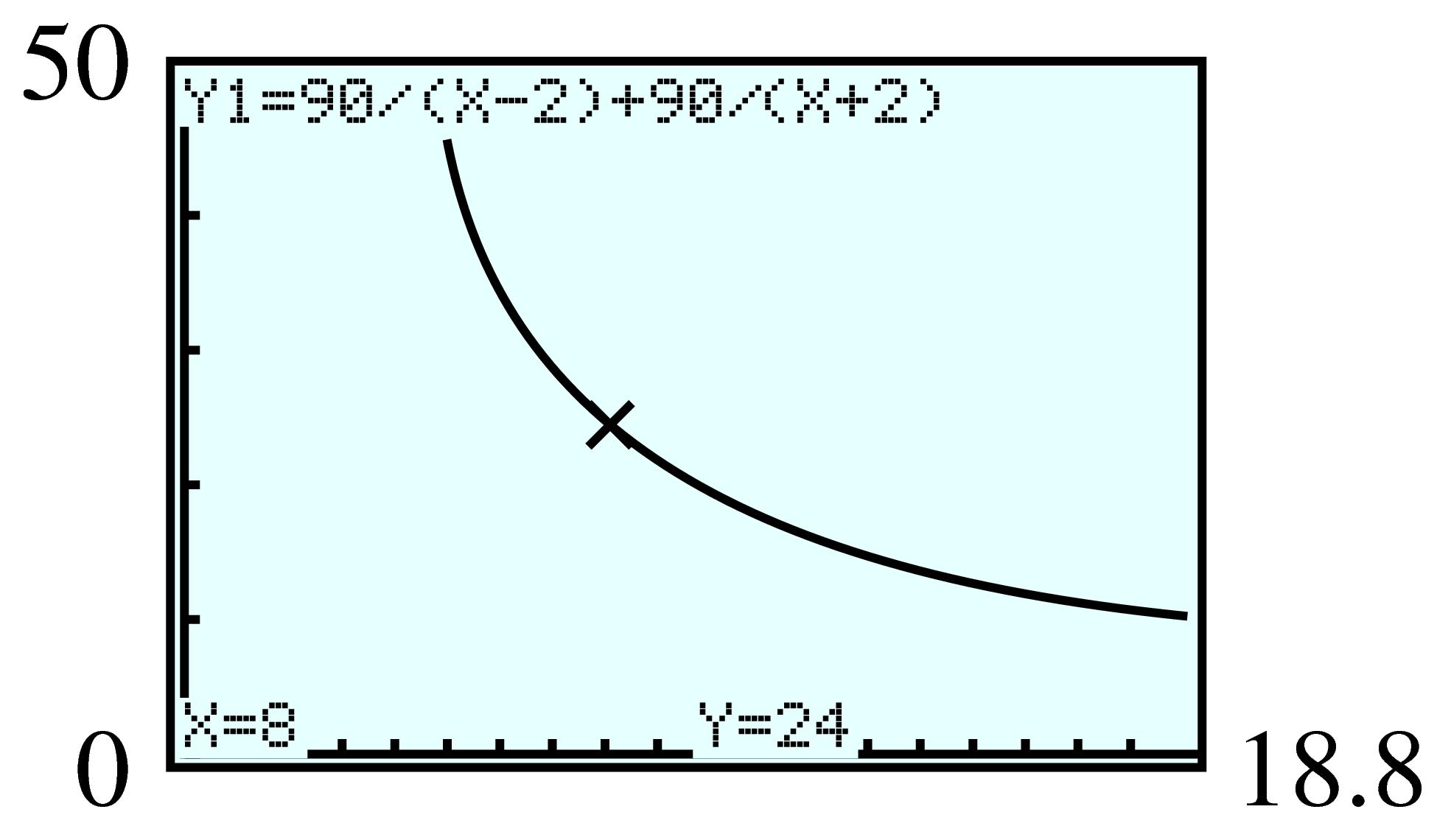
Rate Time Distance

P waves $5.4$ $x$ $y$

S waves $3$ $x+90$ y
$\displaystyle y = 3 (x + 90)$
$\displaystyle y = 5.4x$
$(112.5, 607.5)\text{:}$ The seismograph is $607.5$ miles from the earthquake.

31.

Answer.

$(-4.6, 52)$

33.

Answer.

$(7.15, 4.3)$

8.2 Systems of Linear Equations in Three Variables
Homework 8.2

1.

Answer.

$(1, 2, -1) $

3.

Answer.

$(2, -1, -1) $

5.

Answer.

$(4, 4, -3) $

7.

Answer.

$(2, -2, 0)$

9.

Answer.

$(0, -2, 3)$

11.

Answer.

$(-1, 1, -2)$

13.

Answer.

$\left(\dfrac{1}{2},\dfrac{2}{3}, -3 \right) $

15.

Answer.

$(4, -2, 2) $

17.

Answer.

$(1, 1, 0) $

19.

Answer.

$\left(\dfrac{1}{2}, \dfrac{-1}{2}, \dfrac{1}{3} \right) $

21.

Answer.

Inconsistent

23.

Answer.

$\left(\dfrac{1}{2}, 0, 3 \right) $

25.

Answer.

$(-1, 3, 0) $

27.

Answer.

Inconsistent

29.

Answer.

$\left(\dfrac{1}{2}, \dfrac{1}{2}, 3 \right) $

31.

Answer.

$60$ nickels, $20$ dimes, $5$ quarters

33.

Answer.

$x = 40$ in, $y = 60$ in, $z = 55$ in

35.

Answer.

$0.3$ cup carrots, $0.4$ cup green beans, $0.3$ cup cauliflower

37.

Answer.

$40$ score only, $20$ evaluations, $80$ narrative report

39.

Answer.

$20$ tennis, $15$ Ping Pong, $10$ squash

8.3 Solving Linear Systems Using Matrices
Homework 8.3

1.

Answer.

$\left[ \begin{array}{@{}cc|c@{}} -2 \amp 1 \amp 0 \\ -9 \amp 3 \amp -6 \end{array}\right] $

3.

Answer.

$\left[ \begin{array}{@{}cc|c@{}} 1 \amp 3 \amp 6 \\ 0 \amp -2 \amp 11 \end{array}\right] $

5.

Answer.

$\left[ \begin{array}{@{}ccc|c@{}} 1 \amp 0 \amp -2 \amp 5 \\ 2 \amp 6 \amp -1 \amp 3 \\ 0 \amp -3 \amp 2 \amp -3 \end{array}\right] $

7.

Answer.

$\left[ \begin{array}{@{}ccc|c@{}} 1 \amp 2 \amp 1 \amp -5 \\ 0 \amp 4 \amp -2 \amp 3 \\ 0 \amp -9 \amp 2 \amp 12 \end{array}\right] $

9.

Answer.

$\left[ \begin{array}{@{}cc|c@{}} 1 \amp -3 \amp 2 \\ 0 \amp 7 \amp 0 \end{array}\right] $

11.

Answer.

$\left[ \begin{array}{@{}cc|c@{}} 2 \amp 6 \amp -4 \\ 4 \amp 0 \amp 3 \\ \end{array}\right] $

13.

Answer.

$\left[ \begin{array}{@{}ccc|c@{}} 1 \amp -2 \amp 2 \amp 1 \\ 0 \amp 7 \amp -5 \amp 4 \\ 0 \amp 9 \amp -11 \amp -1 \end{array}\right] $

15.

Answer.

$\left[ \begin{array}{@{}ccc|c@{}} -1 \amp 4 \amp 3 \amp 2 \\ 3 \amp 0 \amp -5 \amp 14 \\ -3 \amp 0 \amp -3 \amp 8 \end{array}\right] $

17.

Answer.

$\left[ \begin{array}{@{}ccc|c@{}} -2 \amp 1 \amp -3 \amp -2 \\ 0 \amp 4 \amp -6 \amp -2 \\ 0 \amp 0 \amp -4 \amp -5 \end{array}\right] $

19.

Answer.

$(2, 3)$

21.

Answer.

$(-2, 1)$

23.

Answer.

$(3, -1)$

25.

Answer.

$\left(\dfrac{-7}{3}, \dfrac{17}{3} \right) $

27.

Answer.

$(1, 2, 2)$

29.

Answer.

$\left(2, \dfrac{-1}{2},\dfrac{1}{2} \right) $

31.

Answer.

$(-3, 1, -3) $

33.

Answer.

$\left(\dfrac{5}{4},\dfrac{5}{2},\dfrac{-1}{2} \right) $

35.

Answer.

$(3, 4, -1, 2)$

37.

Answer.

$\left(\dfrac{5}{3},\dfrac{4}{3},\dfrac{-1}{2},\dfrac{-2}{3} \right) $

39.

Answer.

$(-5, -2, 3, 4, 2) $

41.

Answer.

$\displaystyle p (x) =\dfrac{-7}{6}x^3 + 7x^2 - \dfrac{65}{6}x + 7$
$\displaystyle p (x) =\dfrac{-1}{2}x^3 + 3x^2 - \dfrac{7}{2}x + 3$

43.

Answer.

$p(x) = -2x^4 + x^3 - x^2 + 3x + 5$

45.

Answer.

$\displaystyle 0=1$
No

47.

Answer.

$\displaystyle 0=0$
$\displaystyle a = 9, b = 4, c = 2$
Yes (infinitely many)

8.4 Linear Inequalities
Homework 8.4

1.

Answer.

3.

Answer.

5.

Answer.

7.

Answer.

9.

Answer.

11.

Answer.

13.

Answer.

15.

Answer.

17.

Answer.

19.

Answer.

21.

Answer.

23.

Answer.

25.

Answer.

27.

Answer.

29.

Answer.

31.

Answer.

33.

Answer.

35.

Answer.

37.

Answer.

39.

Answer.

41.

Answer.

8.5 Linear Programming
Homework 8.5

1.

Answer.

The graph of $12 = 3x + 4y$ does not intersect the set of feasible solutions.

3.

Answer.

$(8, 2)\text{;}$ $$32$

5.

Answer.

$(2,0) $

7.

Answer.

$$22$
$\displaystyle (8, 0)$
$$32$

9.

Answer.

$(1,4) \text{;}$ $7$
$(4,5) \text{;}$ $17$

11.

Answer.

$(0,5) \text{;}$ $-10$
$(5,0) \text{;}$ $25$

13.

Answer.

b. $(0,0) \text{;}$ $0\hphantom{000}$c. $(3,2) \text{;}$ $13$

15.

Answer.

b. $(0,14) \text{;}$ $-14\hphantom{000}$c. $(0,0) \text{;}$ $30$

17.

Answer.

b. $(0,8) \text{;}$ $-160\hphantom{000}$c. $(8,0) \text{;}$ $1600$

19.

Answer.

$\displaystyle C = x + 3y$
$\displaystyle x \ge 0, ~y \ge 0, ~x + 2y \ge 250$
$\displaystyle 250$

21.

Answer.

$\displaystyle P = 36x + 24y$
$x \ge 0\text{,}$ $~y \ge 0\text{,}$ $~x + y \le 180\text{,}$ $~2x+y\le 240$
vertices at $(0,0)\text{,}$ $(120,0)\text{,}$ $(60,120)\text{,}$ $(0,180) $
$$5040$

23.

Answer.

$\displaystyle C = 433x + 400y$
$x \ge 0\text{,}$ $~y \ge 0\text{,}$ $~2.4x + 0.8y \ge 3.2\text{,}$ $~2.5x + 5.2y \ge 10$
$967.7$ cal

25.

Answer.

Maximum $17.4\text{;}$ minimum $-8.4$

27.

Answer.

Maximum $4112\text{;}$ minimum $0$

29.

Answer.

Maximum $1908\text{;}$ minimum $0$

8.6 Chapter Summary and Review
Chapter 8 Review Problems

1.

Answer.

$(-1, 2) $

3.

Answer.

$\left(\dfrac{1}{2}, \dfrac{7}{2} \right) $

5.

Answer.

$(12, 0) $

7.

Answer.

Consistent and independent

9.

Answer.

Dependent

11.

Answer.

$(2, 0, -1)$

13.

Answer.

$(2, -5, 3)$

15.

Answer.

$(-2, 1, 3)$

17.

Answer.

$(3,-1)$

19.

Answer.

$(4, 1)$

21.

Answer.

$(-1,0,2)$

23.

Answer.

$(4, 3, 1, 2)$

25.

Answer.

$(2,-1, 5,-3, 4)$

27.

Answer.

$26$

29.

Answer.

$$3181.82$ at $8\%\text{,}$ $$1818.18$ at $13.5\%$

31.

Answer.

$5$ cm, $12$ cm, $13$ cm

33.

Answer.

35.

Answer.

37.

Answer.

39.

Answer.

41.

Answer.

43.

Answer.

45.

Answer.

$20p + 8g \le 120, ~10p + 10g \le 120$

47.

Answer.

(b) $(1, 0)\text{;}$ $18\hphantom{00000}$ (c) $(5, 2)\text{;}$ $186$

49.

Answer.

$20p + 8g\le 120\text{,}$ $10p + 10g \le 120\text{,}$ $p\ge 0\text{,}$ $g \ge 0$
$2$ batches peanut butter cookies; $10$ batches of granola cookies; for $$125$

9 Sequences and Series
9.1 Sequences
Homework 9.1

1.

Answer.

$-4, -3, -2, -1$

3.

Answer.

$\dfrac{-1}{2}, 1, \dfrac{7}{2}, 7$

5.

Answer.

$2, 1.5, 1.\overline{3}, 1.25$

7.

Answer.

$0, 1, 3, 6$

9.

Answer.

$-1, 1, -1, 1$

11.

Answer.

$1, 0, \dfrac{-1}{3}, \dfrac{1}{2}$

13.

Answer.

$1, 1, 1, 1$

15.

Answer.

$a_1 = \dfrac{4}{3}$

17.

Answer.

$a_n = 3a_{n-1}$

19.

Answer.

$a_{n+1}=\dfrac{1}{3}a_{n+2}$

21.

Answer.

$58$

23.

Answer.

$1.415$

25.

Answer.

$8.944$

27.

Answer.

$3, 5, 7, 9, 11$

29.

Answer.

$24, -12, 6, -3, 1.5$

31.

Answer.

$1, 2, 6, 24, 120$

33.

Answer.

$100, 210, 331, 464.1, 610.51$

35.

Answer.

$\displaystyle 14,000; 11,900; 10,115; 8597.75$
$\displaystyle v_1 = 14,000; v_{n+1} = 0.85v_n$

37.

Answer.

$\displaystyle 1.55, 2.00, 2.45, 2.90$
$\displaystyle c_1 = 1.55; c_{n+1} = c_n + 0.45$

39.

Answer.

$\displaystyle 50,000; 50,000; 50,000; 50,000$
$\displaystyle v_1 = v_n$

41.

Answer.

$\displaystyle 10, 18, 24.4, 29.52$
$\displaystyle d_1 = 10; d_{n+1} = 0.8d_n+10$

43.

Answer.

3
6
0, 1, 3, 6, 10
$\displaystyle L_1 = 0, L_{n+1} = n + L_n$

45.

Answer.

$\displaystyle 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987$
$1, 2, 1.5, 1.\overline{6}, 1.6, 1.625, 1.615, 1.619, 1.618, 1.618, 1.618, 1.618, 1.618,$

$1.618, 1.618.$

The quotients approach a limit near $1.618\text{.}$

$\dfrac{1+\sqrt{5}}{2} \approx 1.618033989\text{,}$ the same as the limit above.

47.

Answer.

$a_n$ approaches $1.4142\text{,}$ or $\sqrt{2}\text{.}$

49.

Answer.

$c_n$ approaches $0.64039\text{,}$ or $\dfrac{1+\sqrt{17}}{8}$

51.

Answer.

$s_n$ approaches $2$

9.2 Arithmetic and Geometric Sequences
Homework 9.2

1.

Answer.

Geometric

3.

Answer.

Arithmetic

5.

Answer.

Geometric

7.

Answer.

Neither

9.

Answer.

Geometric

11.

Answer.

Geometric

13.

Answer.

$2, 6, 10, 14$

15.

Answer.

$\dfrac{1}{2}, \dfrac{3}{4}, 1, \dfrac{5}{4}$

17.

Answer.

$2.7, 1.9, 1.1, 0.3$

19.

Answer.

$5, -10, 20, -40$

21.

Answer.

$9, 6, 4, \dfrac{8}{3}$

23.

Answer.

$60, 24, 9.6, 3.84 $

25.

Answer.

$15, 19, 23, \cdots, 3 + (n-1)4$

27.

Answer.

$-13, -17, -21, \cdots, -1-4(n-1)$

29.

Answer.

$\dfrac{16}{3}, \dfrac{32}{3}, \dfrac{64}{3}, \cdots, \dfrac{2}{3}(2)^{n-1}$

31.

Answer.

$\dfrac{-1}{2}, \dfrac{1}{4}, \dfrac{-1}{8}, \cdots, 4(\dfrac{-1}{2})^{n-1}$

33.

Answer.

$7.5$

35.

Answer.

$\dfrac{3}{128}$

37.

Answer.

$3$

39.

Answer.

$13$

41.

Answer.

$s_n = 3+2(n-1)$

43.

Answer.

$x_n = -3(n-1)$

45.

Answer.

$d_n = 24(\dfrac{-1}{2})^{n-1}$

47.

Answer.

$w_n = 2^{n-1}$

49.

Answer.

$\displaystyle s_n = 30+2(n-1)$
128

51.

Answer.

$\displaystyle d_n = 50+5(n-1)$
$115

53.

Answer.

$\displaystyle V_n = 500(1.05)^{n}$
$1203.31

55.

Answer.

$\displaystyle c_n = 100(0.8)^n$
1.15 kg

9.3 Series
Homework 9.3

1.

Answer.

$99$

3.

Answer.

$106\dfrac{2}{3}$

5.

Answer.

$141$

7.

Answer.

$410$

9.

Answer.

$-95.8125$

11.

Answer.

$89.88075$

13.

Answer.

Arithemtic; 2550

15.

Answer.

Geometric; 2046

17.

Answer.

Neither; 784

19.

Answer.

Arithmetic; 1071

21.

Answer.

Geometric; 8.996

23.

Answer.

$1938$

25.

Answer.

$78$

27.

Answer.

10.125 ft
107.25 ft

29.

Answer.

$7,400,000

31.

Answer.

66.25 sec

33.

Answer.

$6,504,532.78

35.

Answer.

4540.7 sec

37.

Answer.

$15,269.50

39.

Answer.

$10,737,418.23

9.4 Infinite Geometric Series
Homework 9.4

1.

Answer.

$1^2+2^2+3^2+4^2$

3.

Answer.

$3+4+5$

5.

Answer.

$1(2)+2(3)+3(4)+4(5)$

7.

Answer.

$\dfrac{-1}{2}+\dfrac{1}{2^2}-\dfrac{1}{2^3}+\dfrac{1}{2^4}$

9.

Answer.

$\displaystyle{\sum_{k=1}^{4} (2k-1)}$

11.

Answer.

$\displaystyle{\sum_{k=1}^{4} 5^{2k-1}}$

13.

Answer.

$\displaystyle{\sum_{k=1}^{5} k^2}$

15.

Answer.

$\displaystyle{\sum_{k=1}^{5} \dfrac{k}{k+1}}$

17.

Answer.

$\displaystyle{\sum_{k=1}^{6} \dfrac{k}{2k-1}}$

19.

Answer.

$\displaystyle{\sum_{k=1}^{\infty} \dfrac{2^{k-1}}{k}}$

21.

Answer.

Neither; 97

23.

Answer.

Neither; $\dfrac{25}{12}$

25.

Answer.

Neither; 100

27.

Answer.

Geometric; $5,230,176,600$

29.

Answer.

Atithmetic; $20,100$

31.

Answer.

Neither; 441

33.

Answer.

Arithemetic; 1364

35.

Answer.

Arithmetic; $-520$

37.

Answer.

Geometric; $24,414,062$

39.

Answer.

Geometric; $104.76$

41.

Answer.

$1$

43.

Answer.

$14.12$

45.

Answer.

$\dfrac{5}{2}$

47.

Answer.

$\dfrac{3}{8}$

49.

Answer.

$\dfrac{4}{9}$

51.

Answer.

$\dfrac{31}{99}$

53.

Answer.

$2\dfrac{410}{999}$

55.

Answer.

$\dfrac{29}{225}$

57.

Answer.

120 in

59.

Answer.

30 ft

9.5 The Binomial Expansion
Homework 9.5

1.

Answer.

$51; 101$

3.

Answer.

$100; 50$

5.

Answer.

11 rows

$n=0$	$\hphantom{0000}$	$1$
$n=1$		$1\hphantom{000}1$
$n=2$		$1\hphantom{000}2\hphantom{000}1$
$n=3$		$1\hphantom {000}3\hphantom{000} 3 \hphantom{000}1$
$n=4$		$1\hphantom {000}4\hphantom{000} 6 \hphantom{000}4\hphantom{000}1$
$n=5$		$1\hphantom {000} 5\hphantom{ii0} 10 \hphantom{00}10 \hphantom{0ii}5 \hphantom{000}1$
$n=6$		$1\hphantom {000} 6\hphantom{ii0} 15 \hphantom{00}20 \hphantom{0ii}15 \hphantom{000} 6\hphantom{ii0}1$
$n=7$		$1\hphantom {000} 7\hphantom{ii0} 21 \hphantom{00}35 \hphantom{0ii}35 \hphantom{000} 21 \hphantom{00} 7\hphantom{ii0}1$
$n=8$		$1\hphantom {000} 8\hphantom{ii0} 28 \hphantom{00}56 \hphantom{0ii}70 \hphantom{ii0} 56 \hphantom{00}28 \hphantom{000} 8\hphantom{ii0}1$
$n=9$		$1\hphantom {000} 9\hphantom{ii0} 36 \hphantom{00}84 \hphantom{0ii}126 \hphantom{000} 126 \hphantom{000} 84 \hphantom{00} 36 \hphantom{0ii} 9 \hphantom{ii0}1$
$n=10$		$1\hphantom {000} 10\hphantom{ii0} 45 \hphantom{00} 120 \hphantom{0ii}210 \hphantom{000} 252 \hphantom{ii0} 210 \hphantom{ii0} 120\hphantom{ii0} 45 \hphantom{00} 10 \hphantom{0ii} 1$

7.

Answer.

$x^5 + 15x^4 + 90x^3 + 270x^2 + 405 x +243$

9.

Answer.

$z^4 - 12z^3 + 54z^2 - 108z + 81$

11.

Answer.

$8x^3 - 6x^2y + \dfrac{3}{2}xy^2 - \dfrac{1}{8}y^3$

13.

Answer.

$x^{14} - 21x^{12} + 189x^{10} - 945x^8 + 2835x^6 - 5103x^4 + 5103x^2 -2187$

15.

Answer.

$x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5$

17.

Answer.

$p^4 - 8p^3q +24p^2q^2 - 32pq^3 - 16p^4$

19.

Answer.

$2 + 150t^2$

21.

Answer.

$z^5 - 5z^3 + 10z - 10z^{-1} + 5z^{-3} - z^{-5}$

23.

Answer.

$\displaystyle 5\cdot 4\cdot 3\cdot 2\cdot 1 = 120$
$\displaystyle \dfrac{9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1} = 72$
$\displaystyle \dfrac{(5\cdot 4\cdot 3\cdot 2\cdot 1)(7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1)}{12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1} = \dfrac{1}{792}$
$\displaystyle \dfrac{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{(2\cdot 1)(6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1)} = 28$

25.

Answer.

$\displaystyle 84$
$\displaystyle 220$
$\displaystyle 190$
$\displaystyle 2002$

27.

Answer.

$\displaystyle 1-14x+84x^2$
$\displaystyle 64-192x+240x^2$

29.

Answer.

$-2560u^4-320u^2-2$

31.

Answer.

$\displaystyle 1-30c+375c^2-2500c^3$
$\displaystyle 1-34c+495c^2-4000c^3$

33.

Answer.

$56$

35.

Answer.

$77,520$

37.

Answer.

$-101,376$

39.

Answer.

$1680$

41.

Answer.

$-84$

43.

Answer.

$1,~11,~121,~1331,~14641.~~$ The digits of the terms in the sequence correspond to the numbers in the first five rows of Pascal’s triangle. If $11^n = (10+1)^n$ is expanded as a binomial, each term is the product of a number from Pascal’s triangle times a power of 10 times a power of 1.

9.6 Chapter Summary and Review
Chapter 9 Review Problems

1.

Answer.

$\dfrac{1}{2}, \dfrac{2}{5}, \dfrac{3}{10}, \dfrac{4}{17}$

3.

Answer.

$5, 2, -1, -4, -7$

5.

Answer.

$\displaystyle 1584, 1393.92, 1226.65, 1079.45$
$\displaystyle a_1 = 1584,~ a_{n+1} = 0.88a_n$

7.

Answer.

$\displaystyle 30, 37.5, 43.125, 47.34375$
$\displaystyle a_1 = 30,~ a_{n+1} = 0.75a_n +15$

9.

Answer.

$x_7 = -25$

11.

Answer.

$32$

13.

Answer.

$\dfrac{-81}{8}$

15.

Answer.

$136$

17.

Answer.

$68$

19.

Answer.

Geometric; $\dfrac{-1}{16}, \dfrac{1}{32}, \dfrac{-1}{64}, \dfrac{1}{128};~a_n = (-1)^n (\dfrac{1}{2})^{n-1}$

21.

Answer.

Arithmetic; $-14, -19, -25, -29; ~a_n = 11 - 5n$

23.

Answer.

Geometric; $-16, 32, -64, 128; ~a_n = (-1)^n (2)^{n-1}$

25.

Answer.

Arithmetic; $-1, -5, -9, -13; ~a_n = 7-4n$

27.

Answer.

Geometric; $-48, 192, -768, 3072, ~a_n = 12(-4)^{n-1}$

29.

Answer.

$2(1) + 3(2) + 4(3) + 5(4)$

31.

Answer.

$~~\displaystyle{\sum_{k=1}^{12} ~(2^k - 1)}$

33.

Answer.

Arithmetic; 210

35.

Answer.

Arithmetic; 57

37.

Answer.

Geometric; $\dfrac{121}{243}$

39.

Answer.

Neither; $-4$

41.

Answer.

Geometric; $\dfrac{-9}{5}$

43.

Answer.

$\dfrac{64}{27}$ ft

45.

Answer.

810
$\displaystyle ~~\displaystyle{\sum_{n=2}^{16} 6n}$

47.

Answer.

84 ft

49.

Answer.

$\dfrac{29}{9}$

51.

Answer.

$x^5 - 10x^4 + 40x^3 - 80x^2 + 80x -32$

53.

Answer.

$20$

55.

Answer.

$21$

57.

Answer.

$32$

59.

Answer.

$-672$

Prev Top Next

\(h\)	\(0\)	\(3\)	\(6\)	\(9\)	\(10\)
\(T\)	\(65\)	\(80\)	\(95\)	\(110\)	\(115\)

\(w\)	\(0\)	\(4\)	\(8\)	\(12\)	\(16\)
\(A\)	\(250\)	\(190\)	\(130\)	\(70\)	\(10\)

Miles Driven	\(4000\)	\(8000\)	\(12,000\)	\(16,000\)	\(20,000\)
Cost ($)	\(5500\)	\(6000\)	\(6500\)	\(7000\)	\(7500\)

\(x\)	\(0\)	\(10\)	\(20\)	\(30\)	\(40\)	\(50\)	\(60\)	\(70\)	\(80\)	\(90\)	\(100\)
\(f(x)\)	\(800\)	\(840\)	\(840\)	\(800\)	\(720\)	\(600\)	\(440\)	\(240\)	\(0\)	\(-280\)	\(-600\)

\(x\)	\(50\)	\(51\)	\(52\)	\(53\)	\(54\)	\(55\)	\(56\)	\(57\)	\(58\)
\(f(x)\)	\(600\)	\(585.8\)	\(571.2\)	\(556.2\)	\(540.8\)	\(525\)	\(508.8\)	\(492.2\)	\(475.2\)

\(x\)	\(56\)	\(56.1\)	\(56.2\)	\(56.3\)	\(56.4\)	\(56.5\)	\(56.6\)
\(f(x)\)	\(508.8\)	\(507.158\)	\(505.512\)	\(503.862\)	\(502.208\)	\(500.55\)	\(498.888\)

\(x\)	\(-4\)	\(-2\)	\(3\)	\(5\)
\(g(x)\)	\(4.5\)	\(5.7\)	\(5.2\)	\(3.3\)

\(n\)	\(100\)	\(500\)	\(800\)	\(1200\)	\(1500\)
\(C\)	\(4000\)	\(12,000\)	\(18,000\)	\(26,000\)	\(32,000\)

\(d\)	\(V\)
\(-5\)	\(-4.8\)
\(-2\)	\(-3\)
\(1\)	\(-1.2\)
\(6\)	\(1.8\)
\(10\)	\(4.2 \)

\(r\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(V\)	\(8.8\)	\(35.2\)	\(79.2\)	\(140.7\)	\(219.9\)	\(316.7\)	\(431.0\)	\(563.0\)

\(x\)	\(4 \)	\(1 \)	\(\frac{1}{4} \)	\(0 \)	\(\frac{1}{4} \)	\(1 \)	\(4 \)
\(y\)	\(-2\)	\(-1 \)	\(-\frac{1}{2} \)	\(0 \)	\(\frac{1}{2} \)	\(1 \)	\(2 \)

\(\text{Price of item} \)	\(18\)	\(28\)	\(12\)
\(\text{Tax} \)	\(1.17\)	\(1.82\)	\(0.78\)
\(\text{Tax}/\text{Price} \)	\(\alert{0.065}\)	\(\alert{0.065}\)	\(\alert{0.065}\)

\(\text{Width (feet)} \)	\(2\)	\(2.5\)	\(3\)
\(\text{Length (feet)} \)	\(12\)	\(9.6\)	\(8\)
\(\text{Length}\times \text{width} \)	\(\alert{24}\)	\(\alert{24}\)	\(\alert{24}\)

\(4\)	\(\alert{30}\)
\(\alert{8} \)	\(15\)
\(20\)	\(6\)
\(30\)	\(\alert{4} \)
\(\alert{40} \)	\(3\)

\(x\)	\(1\)	\(0.5\)	\(0.25\)	\(0.125\)	\(0.0625\)
\(x^{-2}\)	\(1 \)	\(4 \)	\(16 \)	\(64 \)	\(256 \)

\(t\)	\(4\)	\(8\)	\(20\)	\(40\)
\(S\)	\(32 \)	\(64\)	\(160\)	\(320\)

\(x\)	\(50\)	\(125\)
\(y\)	\(9000\)	\(15,000\)

\(C\)	\(15\)	\(-5\)
\(F\)	\(59\)	\(23\)

\(t\)	\(0\)	\(15\)
\(P\)	\(4800\)	\(6780\)

\(d\) (nautical miles)	\(4\)	\(5\)	\(7\)	\(10\)
\(P\) (picowatts)	\(31.3 \)	\(12.8\)	\(3.3\)	\(0.8\)

Element	Carbon	Potassium	Cobalt	Technetium	Radium
Mass number, \(A\)	\(14\)	\(40\)	\(60\)	\(99\)	\(226\)
Radius, \(r\) (\(10^{-13}\) cm)	\(3.1\)	\(4.4\)	\(5.1\)	\(6\)	\(7.9\)

Percent Ammonia
	Pressure (atmospheres)
Temperature (\(\degree\)C)	\(50\)	\(100\)	\(150\)	\(200\)	\(250\)	\(300\)	\(350\)	\(400\)
\(350\)	\(25\)	\(38\)	\(46\)	\(53\)	\(58\)	\(62\)	\(66\)	\(68\)
\(400\)	\(16\)	\(26\)	\(33\)	\(38\)	\(45\)	\(48\)	\(53\)	\(56\)
\(450\)	\(9\)	\(17\)	\(23\)	\(28\)	\(32\)	\(37\)	\(40\)	\(43\)
\(500\)	\(6\)	\(11\)	\(16\)	\(20\)	\(23\)	\(27\)	\(29\)	\(32\)
\(550\)	\(4\)	\(8\)	\(11\)	\(14\)	\(17\)	\(19\)	\(22\)	\(24\)

\(x\)	\(16\)	\(\dfrac{1}{4} \)	\(3\)	\(100\)
\(Q(x)\)	\(4096 \)	\(\dfrac{1}{8} \)	\(4\sqrt{3^5}\approx 62.35 \)	\(400,000\)

\(x\)	\(y=2^x\)	\(f(x)\)	\(g(x)\)
\(-2\)	\(\dfrac{1}{4} \)	\(\dfrac{1}{8} \)	\(\dfrac{-3}{4} \)
\(-1\)	\(\dfrac{1}{2} \)	\(\dfrac{1}{4} \)	\(\dfrac{-1}{2} \)
\(0\)	\(1 \)	\(\dfrac{1}{2} \)	\(0 \)
\(1\)	\(2 \)	\(1 \)	\(1 \)
\(2\)	\(4 \)	\(2 \)	\(3 \)

\(x\)	\(y=3^x\)	\(f(x)\)	\(g(x)\)
\(-2\)	\(\dfrac{1}{9} \)	\(\dfrac{-1}{9} \)	\(9 \)
\(-1\)	\(\dfrac{1}{3} \)	\(\dfrac{-1}{3} \)	\(3 \)
\(0\)	\(1 \)	\(-1 \)	\(1 \)
\(1\)	\(3 \)	\(-3 \)	\(\dfrac{1}{3} \)
\(2\)	\(9 \)	\(-9 \)	\(\dfrac{1}{9} \)

\(x\)	\(f(x)=x^2\)	\(g(x)=2^x \)
\(-2\)	\(4\)	\(\frac{1}{4} \)
\(-1\)	\(1\)	\(\frac{1}{2} \)
\(0\)	\(0\)	1
\(1\)	\(1\)	\(2\)
\(2\)	\(4\)	\(4\)
\(3\)	\(9\)	\(8\)
\(4\)	\(16\)	\(16\)
\(5\)	\(25\)	\(32\)

\(t\)	\(3.5\)	\(4\)	\(8\)	\(10\)	\(15\)
\(f(t)\)	\(128\)	\(154.75\)	\(184.05\)	\(150.93\)	\(103.96\)

\(x\)	\(x^2\)	\(\log_{10}x\)	\(\log_{10}x^2 \)
\(1\)	\(1\)	\(0\)	\(0\)
\(2\)	\(4\)	\(0.301\)	\(0.602\)
\(3\)	\(9\)	\(0.477\)	\(0.954\)
\(4\)	\(16\)	\(0.602\)	\(1.204\)
\(5\)	\(25\)	\(0.699\)	\(1.398\)
\(6\)	\(36\)	\(0.778\)	\(1.556\)

\(x\)	\(y=\log_e x \)
\(1\)	\(0\)
\(2\)	\(0.693\)
\(4\)	\(1.386\)
\(16\)	\(2.772\)
\(\frac{1}{2} \)	\(-0.693\)
\(\frac{1}{4} \)	\(-1.386\)
\(\frac{1}{16} \)	\(-2.772\)

Appendix G Answers to Selected Exercises

1 Functions and Their Graphs1.1 Linear Models Homework 1.1

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

21.

23.

25.

27.

29.

31.

33.

35.

37.

39.

41.

43.

45.

47.

49.

51.

1.2 Functions Homework 1.2

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

21.

23.

25.

27.

29.

31.

33.

35.

37.

39.

41.

43.

45.

47.

49.

51.

53.

55.

57.

59.

61.

63.

65.

67.

69.

71.

73.

75.

77.

79.

1.3 Graphs of Functions Homework 1.3

1.

3.

5.

7.

9.

11.

13.

15.

17.

19.

1 Functions and Their Graphs
1.1 Linear Models
Homework 1.1

1.2 Functions
Homework 1.2

1.3 Graphs of Functions
Homework 1.3

1.4 Slope and Rate of Change
Homework 1.4

1.5 Linear Functions
Homework 1.5

\(x\)	\(-10\)	\(-5\)	\(0\)	\(5\)	\(10\)	\(15\)	\(20\)
\(f(x)\)	\(0.135\)	\(0.368\)	\(1\)	\(2.718\)	\(7.389\)	\(20.086\)	\(54.598\)

\(x\)	\(0\)	\(0.6931\)	\(1.3863\)	\(2.0794\)	\(2.7726\)	\(3.4657\)	\(4.1589\)
\(e^x\)	\(1 \)	\(2\)	\(4\)	\(8\)	\(16\)	\(32\)	\(64\)

\(n\)	\(0.39\)	\(3.9\)	\(39\)	\(390\)
\(\ln n\)	\(-0.942 \)	\(1.361 \)	\(3.664 \)	\(5.966 \)

\(y\)	\(0\)	\(\frac{-1}{3} \)	\(-1\)	\(-3\)
\(w=g^{-1}(y)\)	\(-1\)	\(0\)	\(1\)	\(2\)

\(x\)	\(4000\)	\(4500\)	\(5000\)	\(5500\)	\(6000\)	\(6500\)	\(7000\)
\(I\)	\(1600\)	\(1350\)	\(1000\)	\(550\)	\(0\)	\(-650\)	\(-1400\)

\(x\)	\(~~1~~\)	\(~~2~~\)	\(~~3~~\)	\(~~4~~\)	\(~~5~~\)
\(y\)	\(1.6\)	\(1.2\)	\(0.8\)	\(0.4\)	\(0\)
\(A\)	\(1.6\)	\(2.4\)	\(2.4\)	\(1.6\)	\(0\)

\(x\)	\(-1\)	\(-0.5\)	\(0\)	\(0.5\)	\(1\)	\(1.5\)	\(2\)
\(f(x) \)	\(0.368 \)	\(0.607 \)	\(1 \)	\(1.649 \)	\(2.718 \)	\(4.482 \)	\(7.389 \)
\(p(x) \)	\(0.333\)	\(0.604\)	\(1\)	\(1.646\)	\(2.667\)	\(4.188\)	\(6.333\)

\(v\)	\(-100\)	\(-75\)	\(-50\)	\(-25\)	\(0\)	\(25\)	\(50\)	\(75\)	\(100\)
\(P\)	\(338.15 \)	\(358.92 \)	\(382.41 \)	\(409.19 \)	\(440 \)	\(475.83 \)	\(518.01 \)	\(568.4 \)	\(629.66 \)

\(\frac{1}{s}\)	\(3\)	\(1.5\)	\(1\)	\(0.6\)	\(0.4\)	\(0.3\)	\(0.15\)
\(\frac{1}{v} \)	\(12.5\)	\(7.1\)	\(5\)	\(3.3\)	\(2.6\)	\(2.2\)	\(1.7\)

	Number of tickets	Cost per ticket	Revenue
Adults	\(x\)	\(7.50\)	\(7.50x\)
Students	\(y\)	\(4.25\)	\(4.25y\)
Total	\(82\)	—	\(465.50\)